同余式
同余式是 数论 的基本概念之一,设m是给定的一个正整数,a、b是整数,若满足m| (a-b),则称a与b对模m 同余 ,记为a≡b (mod m),或记为a≡b (m)。 这个式子称为模m的同余式,若m∤ (a-b),则称a、b对模m不同余
同余概念又常表达为: 1.a=b+km (k∈Z); 2.a和b被m除时有相同的 余数

乘法逆元
乘法逆元的定义:在数学领域,对于群G中的任意一个元素a,总存在G中的一个唯一元素a',使得a×a'=a'×a=e,其中e是群G的单位元。这个元素a'被称为a的乘法逆元。在模运算中,如果ab≡1(mod m),那么b就被称为a关于模m的乘法逆元

费马小定理
推导
由费马小定理+乘法逆元可知,a^(mod-2)就是a取模mod的乘法逆元
例题
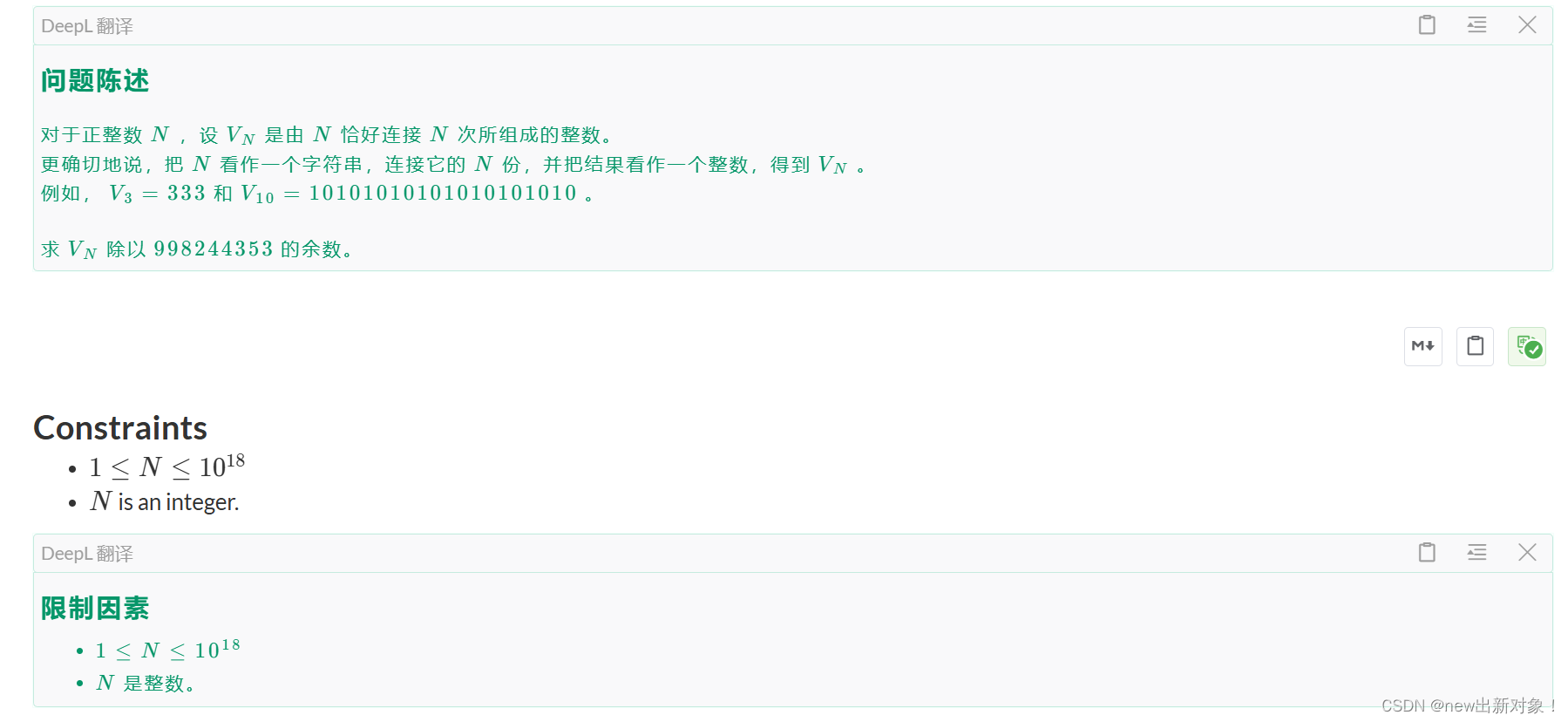
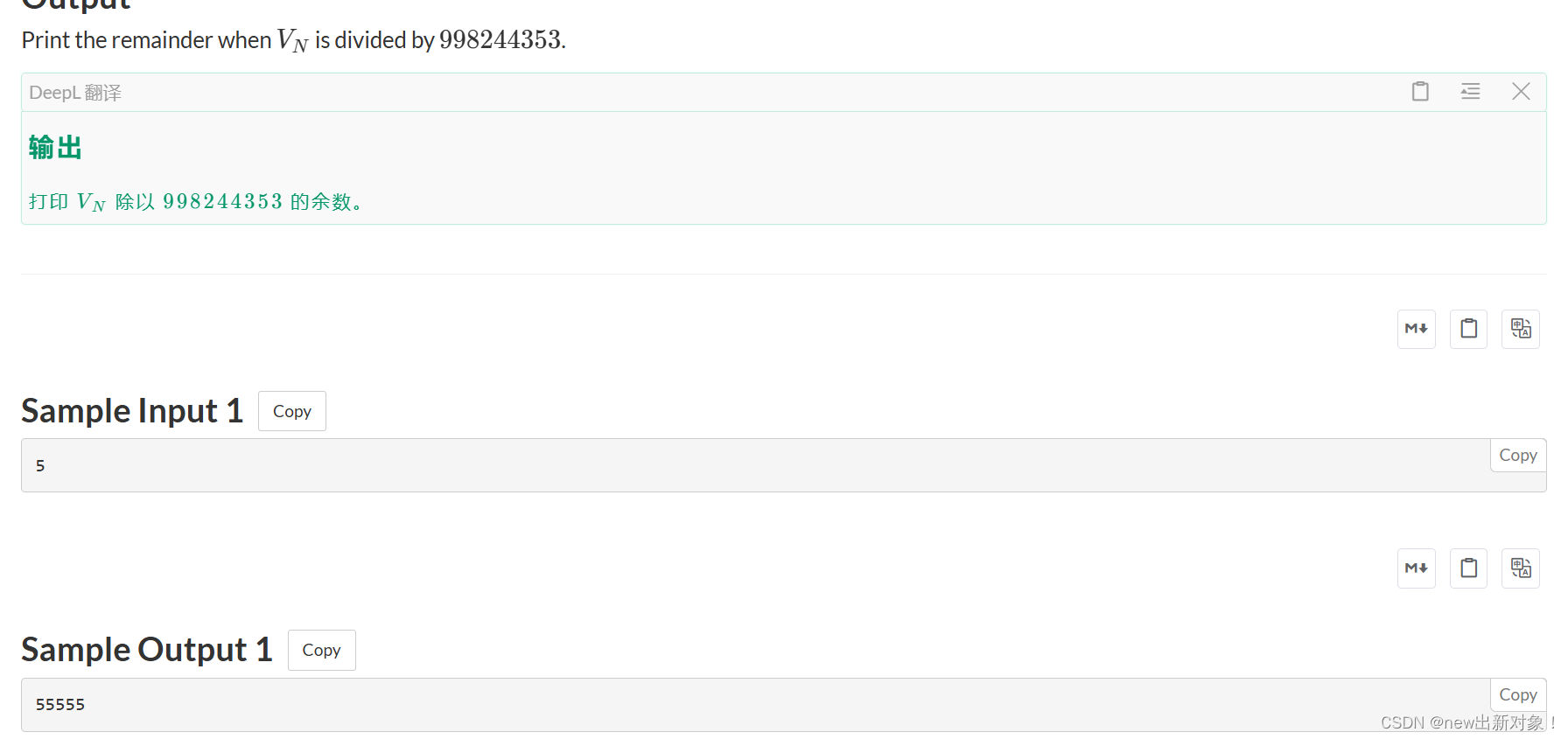
题意:就是说给你一个数,然后问你这个数n这个数被连接n次,然后取模 998244353,所得到的结果是什么,例如样例这个5,5被连接五次就是55555,取模998244353还是55555,所以要输55555
思路,我们发现在连接的过程中,每一项都是后一项的w倍(w是给出的n的倍数,有一位,w就要乘上10,比如说上面这个样例的w就是10)
最终结果是sum=n+w^1*n+w^2*n+......+w^n-1*n;
我们发现每一项都是等比数列,我们可以用等比数列的公式计算出最终结果为n*(w^n-1)/w-1
由取模公式可知,除法取模不能直接取模,我们要借助费马小定理进行逆元,然后得到的
w-1的乘法逆元为(w-1)^(mod-2)
最终结果就变成了n*(w^n-1)*(w-1)^(mod-2),然后在计算过程中对每一步都进行取余数就OK了
当然了,计算这种指数也有方法,用快速幂算法logN的数据绝对不会爆
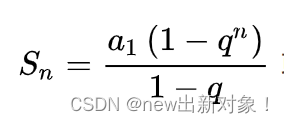
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
int w=1;//统计位数
int mod=998244353;
int sum=0;
//快速幂公式
int fast(int a, int b)
{
long long result = 1;
long long base = a;
while (b > 0)
{
if (b % 2 == 1)
{
result = (result * base) % mod;
}
base = (base * base) % mod;
b /= 2;
}
return result;
}
signed main()
{
cin>>n;
int flag=n;
while(flag)
{
flag/=10;
w*=10;
w%=mod;
}
sum=((n%mod*(fast(w,n)-1)%mod)%mod*fast(w-1,mod-2)%mod)%mod;
cout<<sum;
return 0;
}