【网络流简介】
● 网络流基本概念
网络：网络是一个有向有权图，包含一个源点和一个汇点，没有反平行边。
网络流：是定义在网络边集上的一个非负函数，表示边上的流量。
网络最大流：在满足容量约束和流量守恒的前提下，在流网络中找到一个净输出最大的网络流。
可行流：容量约束、流量守恒。

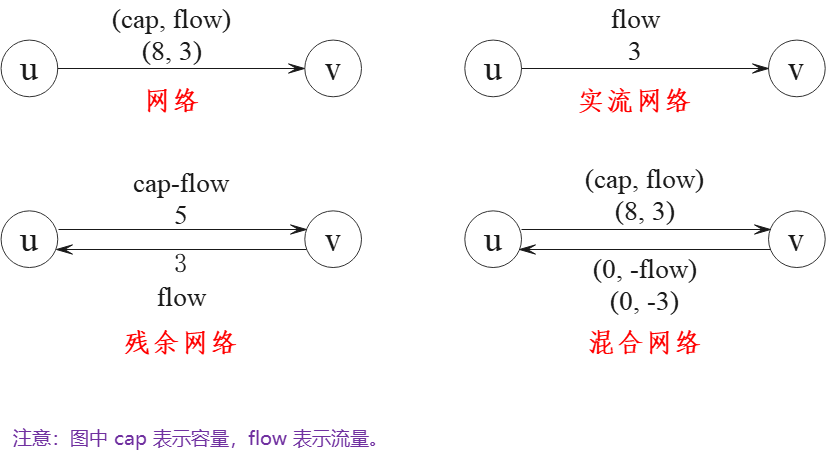
● 网络流常用示意图
在残余网络中找可增广路；
在实流网络中沿可增广路增流，在残余网络中沿可增广路减流。

增广路定理：设 flow 是网络 G 的一个可行流，如果不存在从源点 s 到汇点 t 关于 flow 的可增广路p，则 flow 是 G 的一个最大流。

● 利用“^1”运算表示反向边
由于网络流是有向有权图，因此可以选择链式前向星存图。对一个数连续执行两次“^1”运算后，便会得到自身。这恰好与网络流中“反向边的反向边等于自身”不谋而合。因此，在网络流的算法实现中，我们可以利用“^1”运算来表示反向边。

● 链式前向星：https://blog.csdn.net/hnjzsyjyj/article/details/139369904
val[idx]：存储编号为 idx 的边的值
e[idx]：存储编号为 idx 的结点的值
ne[idx]：存储编号为 idx 的结点指向的结点的编号
h[a]：存储头结点 a 指向的结点的编号