目录
- AOV和AOE
- AOV 有向无环图及其应用(拓扑结构)
- 有向无环图的应用——存放表达式
- 二叉树存放表达式
- 图存放表达式
- AOE 有向无环图及其应用——关键路径
- 1. 事件的最早发生时间
- 事件(顶点)最早发生时间的计算方法:
- 2. 事件允许的最晚发生时间
- 事件(顶点)允许的最晚发生时间的计算方法:
- 3. 活动最早发生时间
- 4. 活动允许的最晚开始时间
AOV和AOE
AOV 有向无环图及其应用(拓扑结构)
AOV网——用顶点表示活动,用弧表示活动间优先关系的有向图称为顶点表示活动的网(Activity On Vertex network),简称AOV网
AOV网中不允许有回路,这意味着某项活动以自己为先决条件
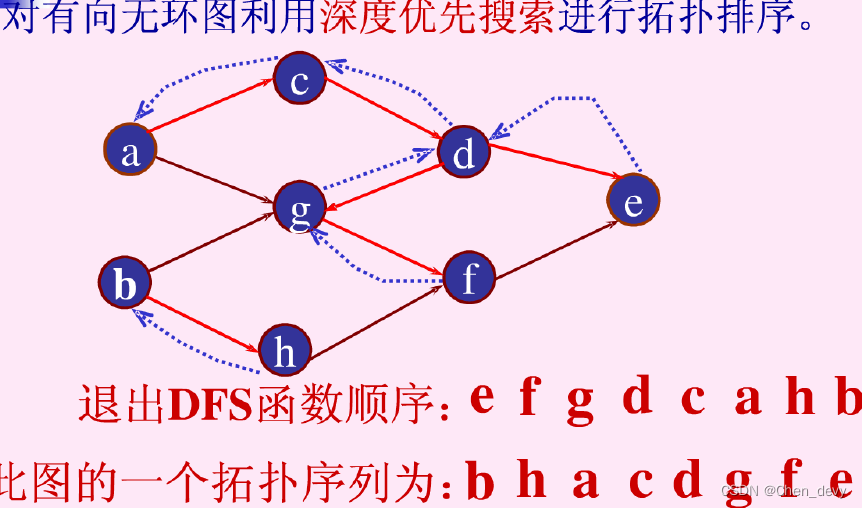
拓扑排序——把AOV网络中各顶点按照它们相互之间的优先关系排列成一个线性序列的过程
检测AOV网中是否存在环方法:对有向图构造其顶点的拓扑有序序列,若网中所有顶点都在它的拓扑有序序列中,则该AOV网必定不存在环。
拓扑排序算法
- 选一个入度为0的顶点,输出;
- 删除该顶点以及由它出发的所有边
- 重复步骤1、2,直到全部顶点输出或不再存在入度为0的顶点;
- 若图中还有剩余顶点未被删除,说明图中有回路,不是一个AOV网
AOV网的拓扑序列不唯一
拓扑排序能够检测图中是否有环存在
图采用邻接表存放;计算所有顶点的入度,存放于一维数组中;
// 结构体
#define MAXSIZE 100
typedef struct ArcNode{
int vex;
struct ArcNode* link;
} ArcNode; //弧
typedef struct VNode{
VertexType data;//顶点信息的数据类型
int id; //顶点的入度
ArcNode* firstarc;
}VNode; //顶点 顶点信息数组
typedef struct {
VNode arc[MAXSIZE];
int vexnum,arcnum;
//有向图
}Graphs;
算法:
int topsort(Graphs T){
//图 T
int q[MAXSIZE], count, h=t=0;//队列指针初始化
//q为队列 用数组 顺序队列
ArcNode * p; // 弧
int u,v;
//1.计算所有顶点入度,将入度为0 的顶点放入队列; count=0;
for(v=0;v<T.vexnum;v++) //遍历所有顶点
T.arcs[v].id=0;//初始化
for (v=0;v<T.vexnum;v++)
for(p=T.arc[v].firstarc; p!=Null; p=p->link){
u=p->vex; //节点的信息存放的位置
T. arc[u].id++; //计算每个节点的入度
}
for (v=0;v<T.vexnum;v++)// 将入度为零的节点 入队
if (T. arc[v].id==0)
q[t++]=v;//自己加判断队列是否会溢出!
//开始拓扑排序
while (h!=t ){ //队列是否为空
v=q[h++]; //位置信息出队
printf(“%d”,v);//打印该位置信息的节点 v是位置信息 此处打印的是位置
count++; //计数
for(p=T.arc[v].firstarc; p!=Null;p=p->link){
//循环读取的是v节点 出度的所有节点
u=p->vex;
T. arc[u].id--;
if (T. arc[u].id==0)
q[t++]=u;//加判断队列是否会溢出!
}//每读取一个 就入队下一个
}
//
if (count<T.vexnum){//如果有节点没有被遍历到过 说明该图不是 联通图
printf(“There is a cycle”);
return 0;
}
else
return 1;
}
//总的时间复杂度为o(n+e)
有向无环图的应用——存放表达式
中缀表达式即运算符在操作数之间的表达式,常见表达式均为中缀表达式。
后缀表达式也叫逆波兰式
前缀表达式也叫波兰式
二叉树存放表达式
二叉树存放表达式 :
波兰式:
+*dj/e+hi
中缀表示:d*j+e/(h+i)
逆波兰式:dj*ehi+/+

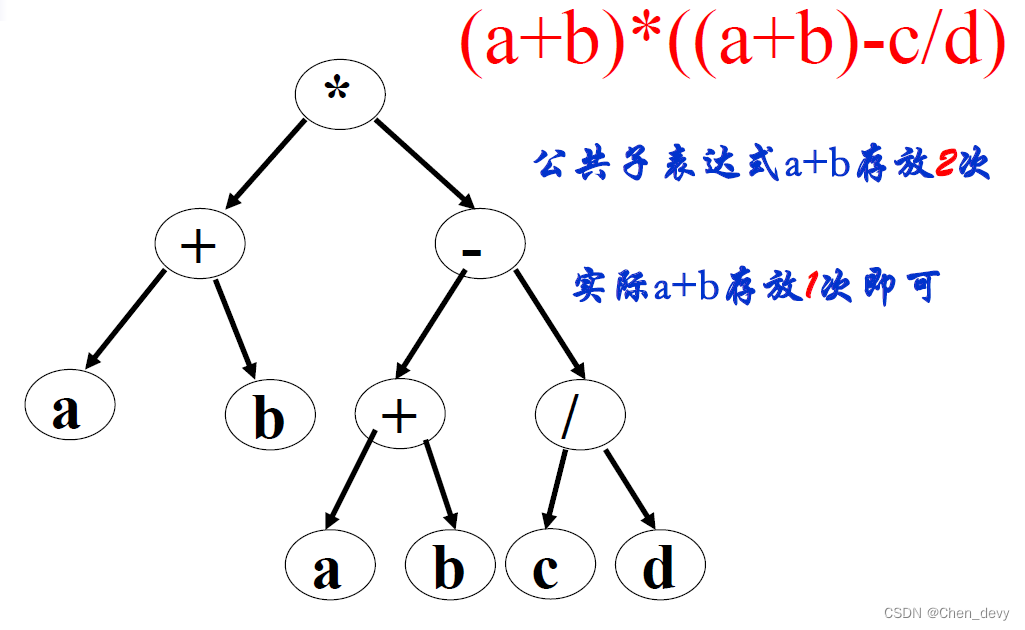
图存放表达式
图存放表达式可以优化公共子表达式,实现公共子表达式共享
特点:只有一个入度为0的顶点
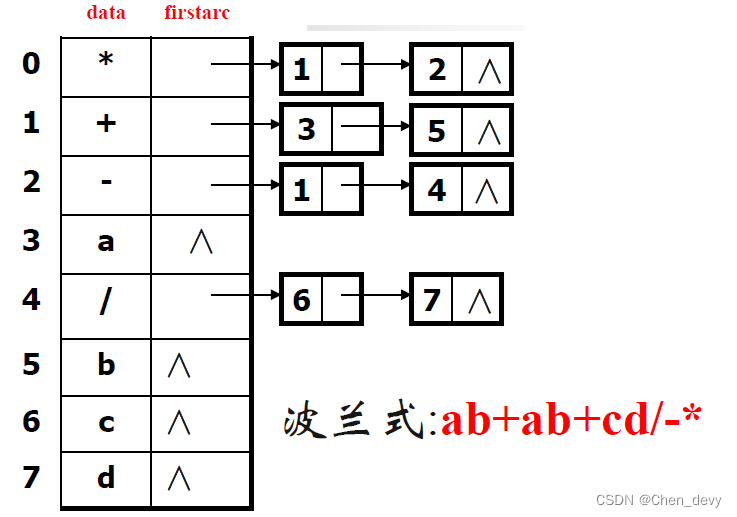
//构造逆波兰式的算法
Void s1(Graphs G){
int id[MAXSIZE];
for(v=0;v<G.vexnum;v++)
id[v]=0;
for (v=0;v<G.vexnum;v++)
for(p= G.arc[v].firstarc; p; p=p->link){
u=p->vex;
id[u]++;
}
for (v=0;v<G.vexnum;v++)
if(id[v]==0)
nibolan(G,v);
}
void nibolan(Graphs G,int v){
//从顶点v出发构造逆波兰式
if(G.arc[v].firstarc==NULL)
printf("%c",G.arc[v].data);
else {
p=G.arc[v].firstarc;
w=p->vex;
nibolan(G,w);
p=p->link;
w=p->vex;
nibolan(G,w);
printf("%c",G.arc[v].data);
}
}
//??
AOE 有向无环图及其应用——关键路径
AOE网:表示工程计划的有向图,其中,顶点表示事件,弧表示活动,弧上的权值表示完成一项活动需要的时间
AOE网中的某些活动可以并行进行,完成工程的最短时间是从开始顶点到完成顶点的最长路径长度。路径长度最长的路径为关键路径。关键路径上所有活动都叫做关键活动。
求解关键路径和关键活动通过事件的最早、最迟发生时间、活动的最早、最迟发生时间完成。
只有在某顶点代表的事件发生后,从该顶点发出去的弧所代表的各项活动才能开始
只有进入某顶点的各条弧代表的活动都已经结束,该顶点所代表的事件才能发生 (*)
1. 事件的最早发生时间
使用一维数组ve[]来保存每一事件的最早发生时间。
事件
v
i
v_i
vi的最早发生时间ve[i]是从开始顶点
v
1
v_1
v1到顶点
v
i
v_i
vi的最长路径长度。
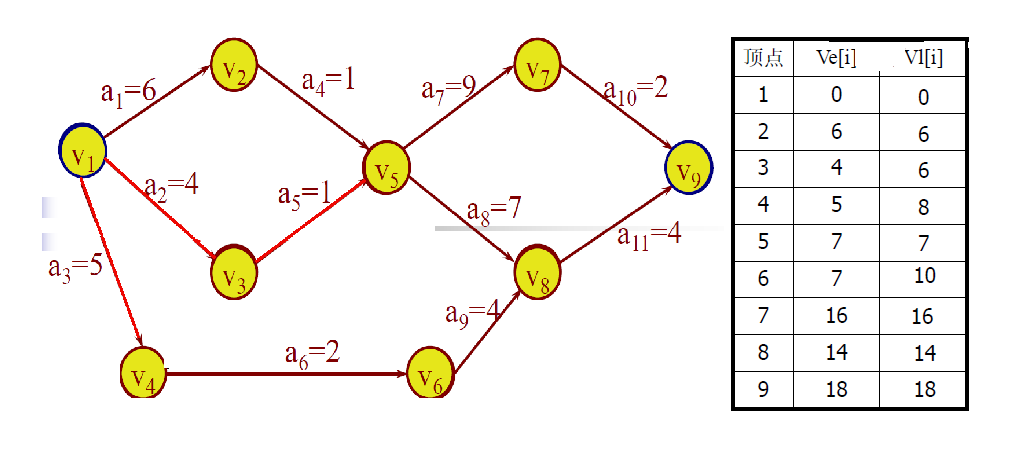
事件(顶点)最早发生时间的计算方法:
从开始顶点
v
1
v_1
v1出发,令ve[1]=0,按拓扑有序求其余各顶点的最早发生时间ve[k](2≤k≤n)
ve[k] = max{ve[j]+dut(<j,k>): <j,k>∈S},dut(<j,k>)表示活动<j,k>的所需的时间,其中S是以顶点v_k为弧头的所有弧的集合。
2. 事件允许的最晚发生时间
一维数组vl []保存每一事件允许的最晚发生时间
事件
v
i
v_i
vi允许的最晚发生时间vl[i]是在保证完成顶点
v
n
v_n
vn在ve[n]时刻发生的前提下,事件
v
i
v_i
vi允许发生的最晚时间,它等于ve[n]减去
v
i
v_i
vi到
v
n
v_n
vn的最长路径长度。
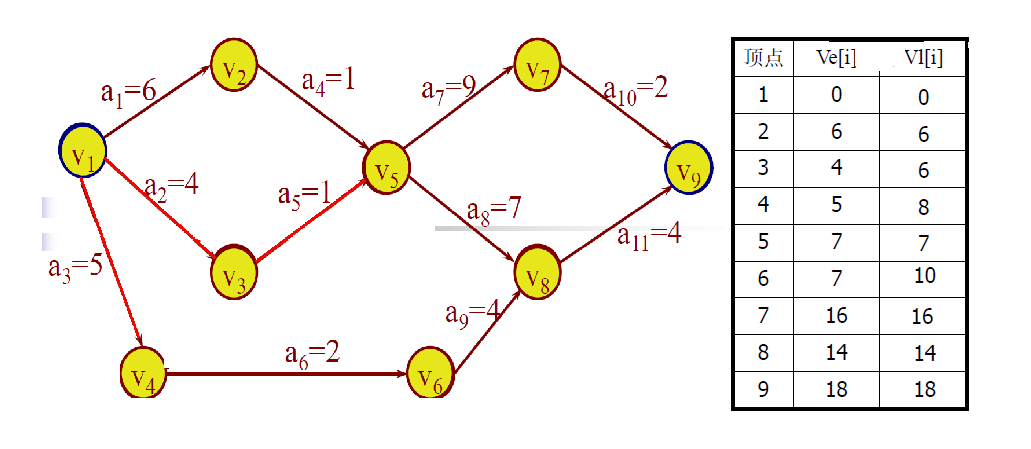
事件(顶点)允许的最晚发生时间的计算方法:
从完成顶点
v
n
v_n
vn出发,令vl[n]=ve[n],按逆拓扑有序求其余各顶点的允许的最晚发生时间vl[i] (n-1≥i≥1)
vl[i]=min{vl[k]-dut(<i,k>): <i,k>∈S}其中S是以顶点vi为弧尾的所有弧的集合。
3. 活动最早发生时间
■ 一维数组e []保存每一活动的最早发生时间
■ 设活动
a
i
a_i
ai用弧
<
v
j
,
v
k
>
<v_j,v_k>
<vj,vk>表示,与
a
i
a_i
ai相联系的权值 dut(<j,k>)用表示,则
a
i
a_i
ai的可能的最早开始时间e[i]等于事件
v
j
v_j
vj可能的最早发生时间ve[j]。
4. 活动允许的最晚开始时间
设活动
a
i
a_i
ai用弧
<
v
j
,
v
k
>
<v_j,v_k>
<vj,vk>表示,与
a
i
a_i
ai相联系的权值dut(<j,k>)用表示,则活动
a
i
a_i
ai允许的最晚开始时间l[i]等于事件
v
k
v_k
vk允许的最晚发生时间vl[k]-dut(<j,k>)。
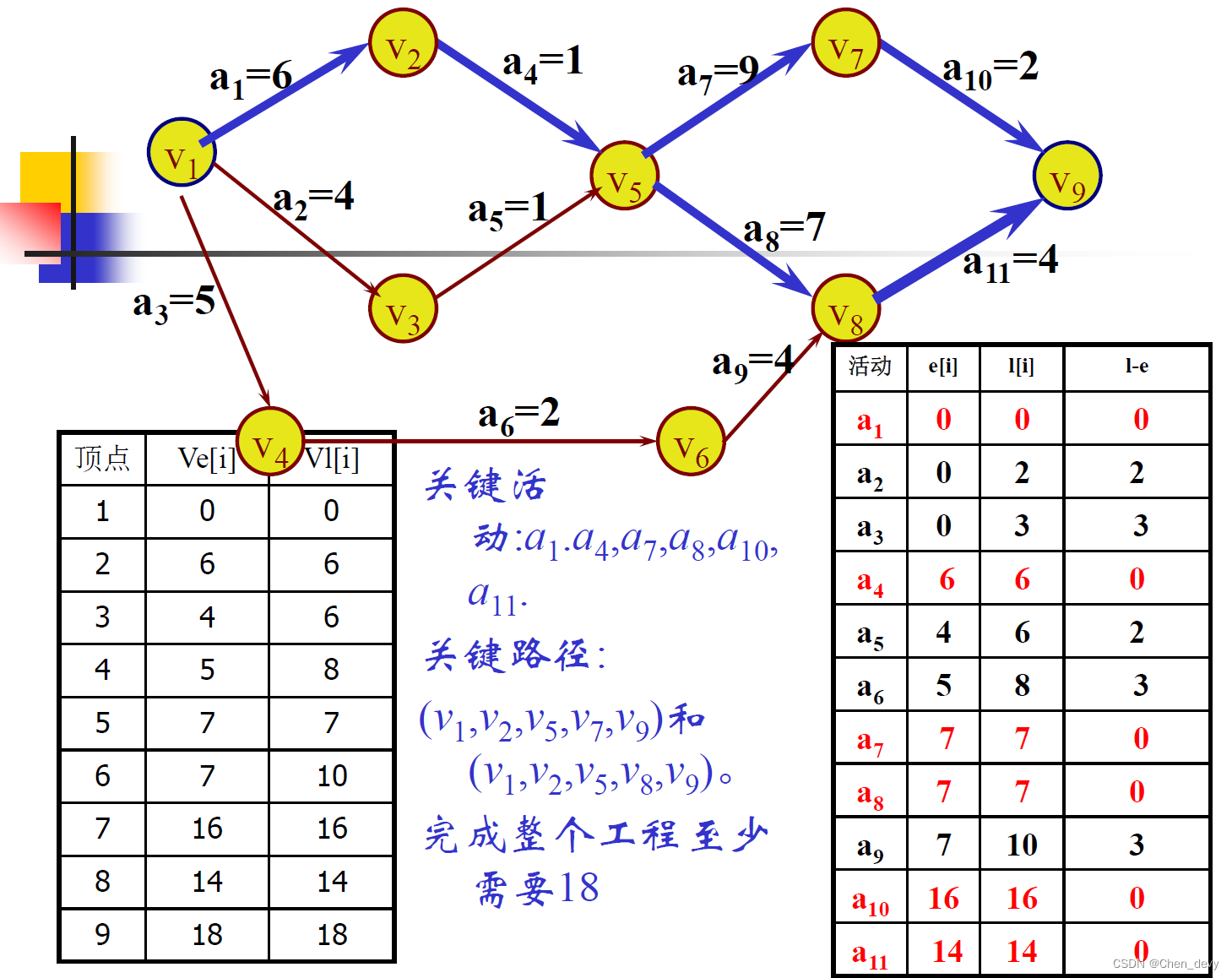
(1)关键路径上所有的活动都是关键活动。因此提前完成非关键活动并不能加快工程的速度。
(2)网络中的关键路径并不唯一,对于有几条关键路径的网来说,仅仅提高某一条关键路径上关键活动的速度,是不能缩短整个工程工期的,而必须同时提高几条关键路径上关键活动的速度。
所以,并不是网中任何一个关键活动的提前完成,整个工程都能提前完成。

![[Elasticsearch] ES更新问题踩坑记录](https://img-blog.csdnimg.cn/img_convert/0353e2818f605320b0f010a8226d0526.webp?x-oss-process=image/format,png)