目录

题目

解题思路

正则表达式代码

动态规划代码

官方解题

---

题目

解题思路

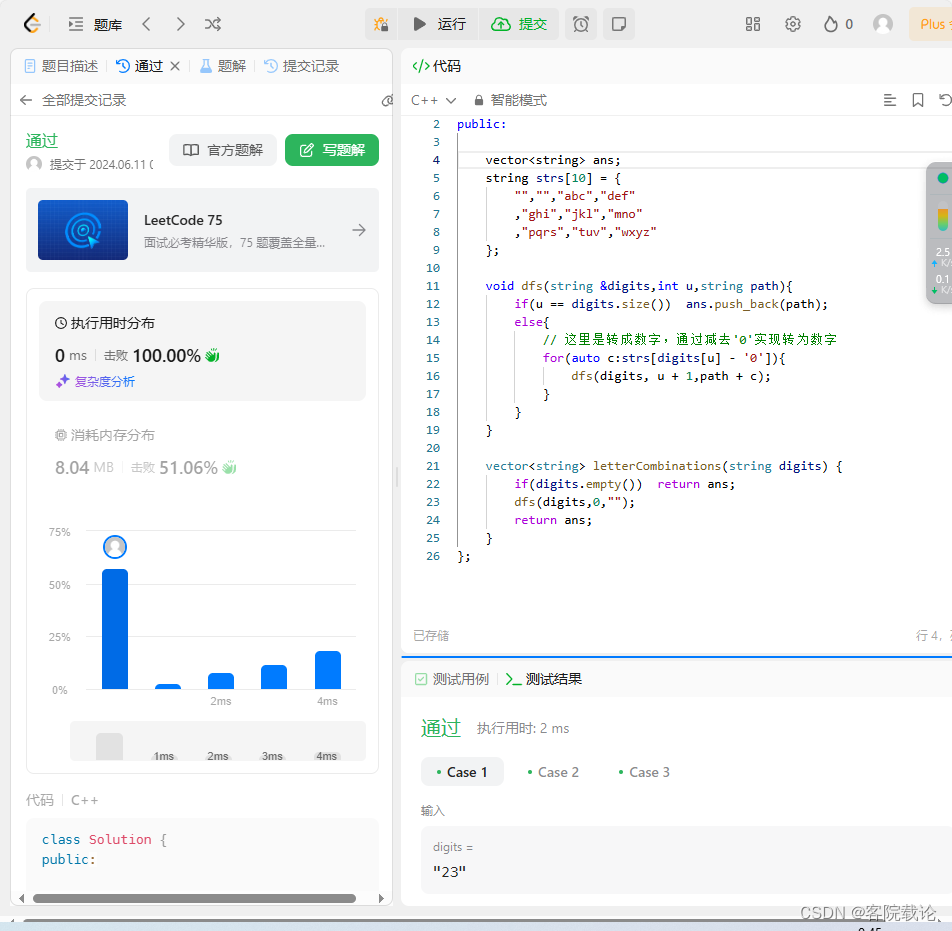
这次也给我捡到狗运了，反正只要一直上传，内存总会遥遥领先的，只要在你速度领先了的情况下。

这次题目还是想当的困难的。我们有两种思路，一种就是使用动态规划，另外一种则是直接使用正则表达式。使用动态规划的话分析起来是想当的复杂。这次的状态转移方程略微有点麻烦，但是我尽可能简短的概述一下。

正则表达式代码

import java.util.regex.Matcher;
import java.util.regex.Pattern;

class Solution {
    public boolean isMatch(String s, String p) {
        while (p.contains("**")) {
            p = p.replace("**", "*");
        }
        Pattern compile = Pattern.compile(String.format("^%s$", p));
        Matcher matcher = compile.matcher(s);
        return matcher.find();
    }
}

那么在说这个正则表达式的原理之前，我们先说明，不要用真正的正则表达式去匹配，还是太慢了。消耗了四百多毫秒，可能有导包的原因，因为默认是没有这个包的。

然后我们解释代码，非常简单，根据他的规则，他就是开头和结尾，所以我们就只需要把开头和结尾的限制符加上就行了^和$，分别识别开头和结尾的，然后我做了个格式化处理让我们的原式可以引进去。

这里需要注意一个问题，因为星号*重复并不是个正常的正则表达式，所以我们需要在他重复出现的时候给他删掉，所以有了我们开头的代码，去除重复的*。然后我们就正常的正则匹配，匹配到了就返回是否找到了就可以了。

这个代码还是十分的简短的。

动态规划代码

class Solution {
    public boolean isMatch(String s, String p) {
        int m = s.length();
        int n = p.length();

        boolean[][] dp = new boolean[m + 1][n + 1];
        dp[0][0] = true;
        for (int i = 0; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (p.charAt(j - 1) == '*') {
                    dp[i][j] = dp[i][j - 2];
                    if (i > 0 && (p.charAt(j - 2) == '.' || s.charAt(i - 1) == p.charAt(j - 2))) {
                        dp[i][j] = dp[i][j] || dp[i - 1][j];
                    }
                } else {
                    if (i > 0 && (p.charAt(j - 1) == '.' || s.charAt(i - 1) == p.charAt(j - 1))) {
                        dp[i][j] = dp[i - 1][j - 1];
                    }
                }
            }
        }
        return dp[m][n];
    }
}

复杂度是的，因为简单来说我们就是通过每个s字符串里的字符都和p里面的字符一个一个匹配，然后加上我们的判断规则，这次创建的dp数组比之前略大1格范围，因为我们做了个结果继承，实际上这也是状态转移方程里的内容。

我们实际比较起来是如此的。如果非*号则就单纯匹配是否为.与是否相等。如果是*号则需要判断*号前一位数符不符合该位置的s字符串的字符相等的情况或者在*号前一位数是否为.号。当然我们不能让i越界，所以判断了i大于0的情况，然后后者是二选一的情况。

如果确定相等了，我们就可以把之前正确的状态继承下来。直到最后的情况，然后如果中途继承状态或者说是转移状态的时候有误，我们则返回没有匹配到。

如果有点不懂可以在debug的时候一步一步执行，然后在最后打印整个dp数组，然后就能看到这个状态转移的过程了。个人感觉比起官方的状态转移方程，看代码运行的过程还是相对比较好理解的。

我们还可以在最前面做个判断，假如俩字符串的长度不相等的情况下且p字符串里面并不含有*号我们可以直接返回false。当然这点优化也是可以不加上的。

官方解题

class Solution {
    public boolean isMatch(String s, String p) {
        int m = s.length();
        int n = p.length();

        boolean[][] f = new boolean[m + 1][n + 1];
        f[0][0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (p.charAt(j - 1) == '*') {
                    f[i][j] = f[i][j - 2];
                    if (matches(s, p, i, j - 1)) {
                        f[i][j] = f[i][j] || f[i - 1][j];
                    }
                } else {
                    if (matches(s, p, i, j)) {
                        f[i][j] = f[i - 1][j - 1];
                    }
                }
            }
        }
        return f[m][n];
    }

    public boolean matches(String s, String p, int i, int j) {
        if (i == 0) {
            return false;
        }
        if (p.charAt(j - 1) == '.') {
            return true;
        }
        return s.charAt(i - 1) == p.charAt(j - 1);
    }
}

官方的代码里面倒是把这个略微简单的逻辑创建了一个新的方法进行返回操作。我倒是感觉还可以再写简便一点，就把我们自己的代码里面的表达式拿出来直接返回那个即可。

如果你觉得还是有点不懂，你可以配合debug一步一步运行的时候顺便代入官方给出的状态转移方程进行计算。

如果对你有帮助的话，不要忘记点赞，收藏。