分发饼干
题意:
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。
思路:
1.先排序; 然后对每个小孩尝试找到让饼干满足的尺寸。
2.一个while循环是针对某个小孩找到第一个能满足要求的饼干。
for(int i = 0 , j = 0; i < g.size() && j < s.size() ; ++ i)
{
while( j< s.size() && s[j] - g[i] < 0 )
{
j++ ;
} // 找到第一个能达到要求的饼干。
// 如果饼干能满足要求那么就j++ ; 并且被满足的小孩总数目加加。
if(j < s.size() && s[j] - g[i] >= 0)
{
manum++ ;
j++ ;
摆动序列
题意是找到最长摆动子序列的长度。
画图
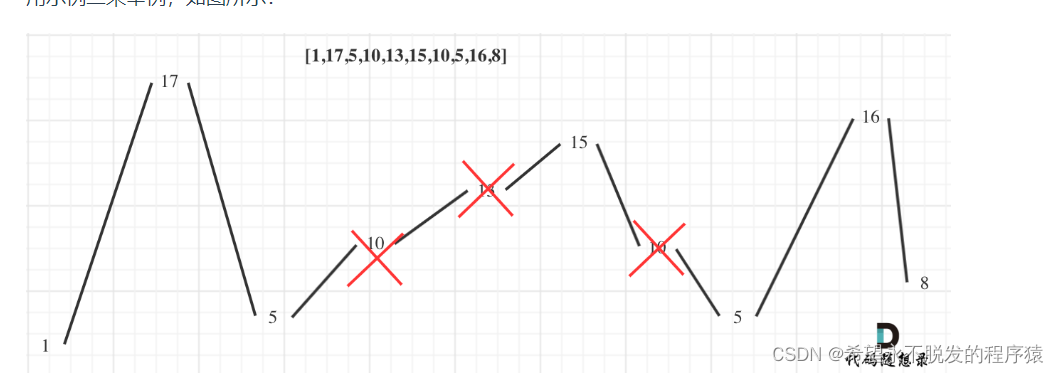
贪心策略:找到局部最优:curdif 和 predif 的规定。 删除单一坡度上的节点这样就只剩下摆动序列,之后找到全局最优。 全局最优是删除全部的单调坡度。
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
int curDiff = 0; // 当前一对差值
int preDiff = 0; // 前一对差值
int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值
for (int i = 0; i < nums.size() - 1; i++) {
curDiff = nums[i + 1] - nums[i];
// 出现峰值
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
result++;
preDiff = curDiff; // 只有在有摆动时,才将predif = curdif
}
}
return result;
}
};
最大子序和
题意:
是找出一个具有最大和的连续子数组。
思路:
局部贪心:每次认为本次寻找的是最大的和。但是如果求得的和小于0;那么就重置为0(证明本次没有找到最大和), 又重新更新最大值。 这就造成了全局贪心:找到全局的最大和。
代码
int maxSubArray(vector<int>& nums)
{
int res =0 , maxres = INT_MIN ;
if(nums.size() == 1)
{
return nums[0] ;
}
for(int i = 0 ;i< nums.size() ; ++ i)
{
res += nums[i] ;
if(maxres < res) // 找到最大值。
{
maxres = res ;
}
if(res <= 0) // 证明本次没找到最大值。
{
res = 0 ;
}
}
return maxres ;
}
买卖股票的最佳时机 II
题意:给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。返回 你能获得的 最大 利润 。
思路:
局部:对每个上升期的股票取得最大利润。
全局:达到最佳最大利润。
具体:如果prices[i-1] > prices[i] 就表示 此时是收割i-1到之前的利润的时候,本次的最大利润就是这个值。 最终得到最大利润。
但是卡哥的更简洁
所以这里列出卡哥的思路:
最终的利润可以分解成每天的利润 ; 如果这天的利润为正加入结果集。
int maxProfit(vector<int>& prices) {
int result = 0;
for (int i = 1; i < prices.size(); i++) {
result += max(prices[i] - prices[i - 1], 0);
}
return result;
}
跳跃游戏
题意:给定一个非负整数nums ; 最初位于数组的第一个下标。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
思路:这个题需要绕一下;从跳跃,转换(映射)到求覆盖范围。
能否到达最后一个下标。并非是求最大的跳跃值。而是求能跳的最大的范围。 这个需要绕一下。
局部:每个元素的跳跃范围 i + nums[i] ; 在这个范围内找到下一次跳跃的最大范围。
之后全局最优。看最大范围是否到最尾元素。
int net =0 , cur = 0 ;
for(int i = 0 ; i < nums.szie() ; ++ i)
{
net = max(nums[i] +i , net) ;
if(cur>=nums.size() -1 )
{
return true;
}
if(i == cur)
{
cur = net ;
}
}
跳跃游戏 II
题意:找到能够跳跃到最后元素的最少次数。
思路:依然是找到能够跳到的最大的范围;
局部最优和全局最优依然是上一题:
每次在该范围内找到下一次的最大的范围。
在每次跳的时候也是改变范围的时候(这也是绕的一点)
int times = 0, cur = 0 , net = 0 ;
for(int i = 0 ; i< nums.size() ; ++ i)
{
if(cur >= nums.size()-1)
{
break ;
}
net = max(nums[i] + i , net); // 计算下一次要遍历的范围的末尾此处是贪心思想的体现。
if(cur == i && cur != nums.size()-1 ) // 如果cur 为 i 时
{
cur = net ;
times ++ ;
}
}
return times ; // 进行返回