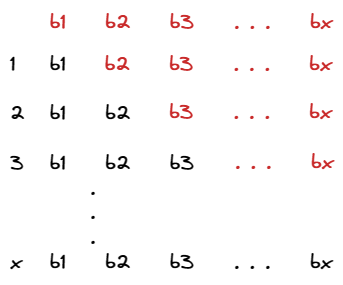CCPC2022（桂林）

news2024/11/26 11:46:31

题目链接：https://codeforces.com/gym/104008

G Group Homework

题目大意：在树上选出两条链，使得在两条链选中的点中，只被一条链选中的点的点权和最大。
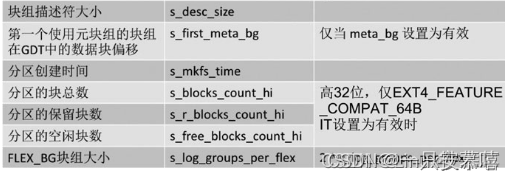
题解：显然两条链要么不相交，要么只相交于一个点。因为如果两条链相交的点多于一个，那一定可以通过交换链的端点的方法使得答案更优。这个结论可以参考出题人给出的示意图，如下图：
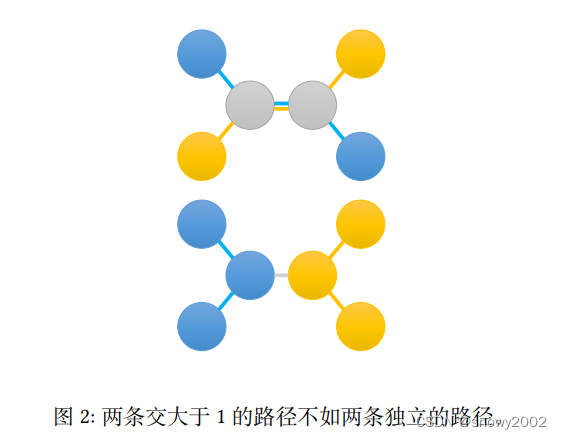
在这里插入图片描述
因此，问题转化为求两条不相交的链的点权和以及求以一个点为根的最大的四个儿子的深度和。我们很容易能够想到可以使用换根dp的方法来解决这两个问题，问题在于码量较大，细节较多，不是很容易实现。
具体讲一下dp的过程，可以先将1号点作为根，维护每个点的深度 h x h_x hx​和最长链的长度 l x l_x lx​，来完成将1看作根结点的求解：
h x = m a x { h s o n } + a x l x = m a x { l s o n , h s o n 1 + h s o n 2 + a x } h_x=max\{ h_{son}\}+a_x \\ l_x=max\{l_{son},h_{son1}+h_{son2}+a_x\} hx​=max{hson​}+ax​lx​=max{lson​,hson1​+hson2​+ax​}
其中， h s o n 1 h_{son1} hson1​和 h s o n 2 h_{son2} hson2​分别表示 x x x的两个最大的儿子深度值。可以通过将 x x x的所有儿子的 h h h值排序的方法来得到。

然后再考虑如何换根，假设当前结点为 x x x，换根结点为 i i i，也就是说，在以 x x x为根的树中， i i i结点是 x x x结点的儿子结点。
我们可以先将 x x x结点的所有儿子的 l l l和 h h h全部取出，然后从大到小排序，这样就可以通过将前四大的 h h h值加和来更新答案，也就是四个最大的儿子的深度，下面考虑两条不相交的链的情况。
首先考虑 x x x结点：换根之后深度 h x h_x hx​显然不能再从 i i i结点转移而来，而应该从其他儿子的最大值中转移得到，所以我们只需要判断 h i h_i hi​结点是否是最大的值即可，是最大值就从次大的 h h h值中转移，不是最大值就不需要更新。最长链 l x l_x lx​显然也不能从结点 i i i来更新，因此先判断 l i l_i li​和 l l l的最大值之间的关系，决定是否从次大的 l l l值中转移。然后还要判断 h i h_i hi​和前二大 h h h值的关系，因为需要用到除了 h i h_i hi​之外的前两大结点进行转移。
h x = m a x { h s o n } + a x     ( s o n ≠ i ) l x = m a x { l s o n , h s o n 1 + h s o n 2 + a x }     ( s o n , s o n 1 , s o n 2 ≠ i ) h_x=max\{ h_{son}\}+a_x ~~~(son\neq i)\\ l_x=max\{l_{son},h_{son1}+h_{son2}+a_x\}~~~(son,son1,son2\neq i) hx​=max{hson​}+ax​   (son=i)lx​=max{lson​,hson1​+hson2​+ax​}   (son,son1,son2=i)
这时，我们求得了以 x x x为根且不含 i i i这个儿子的最长链长度和以 i i i为根且不包含 x x x这个儿子的最长链长度，因此这两条最长链一定不交，可以用来更新答案。
然后再考虑结点 i i i，相当于多了一个儿子 x x x来进行转移：
l i = m a x { l i , l x , h i + h x } h i = m a x { h i , h x + a x } l_i=max\{ l_i,l_x,h_i+h_x \} \\ h_i=max\{h_i,h_x+a_x\} li​=max{li​,lx​,hi​+hx​}hi​=max{hi​,hx​+ax​}
这样，每次换完根之后再将原来的值还原回去，就可以实现换根dp求解了。

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#define time chrono::system_clock::now().time_since_epoch().count()
#include<ext/pb_ds/tree_policy.hpp>
#define clean(x) memset(x,0,sizeof(x))
#define fil(x,n) fill(x,x+1+n,0)
#define inf 2000000009
#define maxn 1000005
using namespace std;
using namespace __gnu_pbds;
mt19937_64 rnd(time);
cc_hash_table<int,int>mp;

int read() {
    int x=1,res=0;
    char c=getchar();
    while(c<'0'||c>'9') {
        if(c=='-') x=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9') {
        res=res*10+(c-'0');
        c=getchar();
    }
    return res*x;
}

signed main()
{
    int n=read();int ans=0;
    vector<int>a(n+1),h(n+1),l(n+1);
    vector<vector<int>>g(n+1);
    
    function<void(int,int)>dfs1=[&](int x,int fa) {
        h[x]=a[x];l[x]=a[x];
        vector<int>son_h;
        for(int i:g[x]) {
            if(i==fa) continue;
            dfs1(i,x);
            h[x]=max(h[i]+a[x],h[x]);
            son_h.push_back(h[i]);
        }
        son_h.push_back(0);
        sort(son_h.rbegin(),son_h.rend());
        for(int i:g[x]) {
            if(i==fa) continue;
            l[x]=max({l[x],l[i],son_h[0]+son_h[1]+a[x]});
        }
    };

    function<void(int,int)>dfs2=[&](int x,int fa) {
        vector<int>son_h,son_l; int res=0;
        for(int i:g[x]) {
            son_h.push_back(h[i]);
            son_l.push_back(l[i]);
        }
        son_h.push_back(0);son_l.push_back(0);son_h.push_back(0);
        sort(son_h.rbegin(),son_h.rend());
        sort(son_l.rbegin(),son_l.rend());
        for(int i=0;i<min(4,(int)son_h.size());i++) res+=son_h[i]; 
        ans=max(ans,res);

        for(int i:g[x]) {
            if(i==fa) continue;
            int pre_x,pre_i,pre_lx,pre_li;
            pre_x=h[x];pre_i=h[i];pre_lx=l[x];pre_li=l[i];
            
            l[x]=a[x];
            if(l[i]==son_l[0]) l[x]=max(l[x],son_l[1]);
            else l[x]=max(l[x],son_l[0]);

            if(son_h[0]==h[i]) h[x]=son_h[1]+a[x];
            else h[x]=son_h[0]+a[x];

            if(son_h[0]==h[i]) l[x]=max(l[x],son_h[1]+son_h[2]+a[x]);
            else if(son_h[1]==h[i]) l[x]=max(l[x],son_h[0]+son_h[2]+a[x]);
            else l[x]=max(l[x],son_h[0]+son_h[1]+a[x]);

            ans=max(ans,l[x]+l[i]);
            l[i]=max({l[i],l[x],h[x]+h[i]});
            h[i]=max(h[x]+a[i],h[i]);

            dfs2(i,x);

            h[x]=pre_x;h[i]=pre_i;
            l[x]=pre_lx;l[i]=pre_li;
        }
    };

    for(int i=1;i<=n;i++) a[i]=read();
    for(int i=1;i<n;i++) {
        int aa=read(),bb=read();
        g[aa].push_back(bb);
        g[bb].push_back(aa);
    }
    if(n==1) {
        puts("0");
        return 0;
    }
    dfs1(1,0);
    dfs2(1,0);
    cout<<ans<<endl;
    return 0;
}

J. Permutation Puzzle

题目大意：构造出一个长度为 n n n排列，使得这个排列满足 m m m个形如 a u < a v a_u<a_v au​<av​的大小关系限制，并且初始有已经填入的数字。

题解：对于形如 a u < a v a_u<a_v au​<av​的关系，我们很容易联系到拓扑排序的性质，我们可以通过建立正向图来进行拓扑排序求解每个位置最小的可能数字 l i l_i li​，通过建立反向图求解每个位置最大的可能数字 r i r_i ri​，然后问题就转化为区间和点的覆盖问题，可以通过优先队列来实现，具体地，将区间按照左端点排序，然后从小到大枚举需要填的数字，每次加入比当前值小的区间，然后用优先队列维护右端点最小的区间作为这个数字应该填入的区间。

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#define time chrono::system_clock::now().time_since_epoch().count()
#include<ext/pb_ds/tree_policy.hpp>
#define inf 2000000009
#define maxn 1000005
#define int long long
using namespace std;
using namespace __gnu_pbds;
mt19937_64 rnd(time);
cc_hash_table<int,int>mp;

int read() {
    int x=1,res=0;
    char c=getchar();
    while(c<'0'||c>'9') {
        if(c=='-') x=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9') {
        res=res*10+(c-'0');
        c=getchar();
    }
    return res*x;
}

void solve() {
    int n=read(),m=read();int ok=1;
    vector<int>a(n+1),l(n+1,-1),r(n+1,1e9),de1(n+1),de2(n+1);
    vector<vector<int>>g1(n+1),g2(n+1);
    for(int i=1;i<=n;i++) {
        a[i]=read();
        if(a[i]!=0) l[i]=r[i]=a[i];
    } 
    for(int i=1;i<=m;i++) {
        int aa=read(),bb=read(); //aa->bb;
        g1[aa].push_back(bb);
        g2[bb].push_back(aa);
        de1[bb]++;de2[aa]++;
    }
    //g1:cal_L   g2:cal_R
    
    auto topo1=[&]() {
        queue<int>q;
        for(int i=1;i<=n;i++) {
            if(de1[i]==0) {
               q.push(i);
               if(a[i]==0) l[i]=1;
            } 
        }
        while(q.size()) {
            int u=q.front();q.pop();
            for(int i:g1[u]) {
                int res=l[u]+1;
                if(res>n) {ok=0;return;};
                if(a[i]!=0&&a[i]<res) {ok=0;return;}
                else if(a[i]!=0) l[i]=a[i];
                else l[i]=max(l[i],res);
                de1[i]--;
                if(de1[i]==0) q.push(i);
            }
        }
    };
    auto topo2=[&]() {
        queue<int>q;
        for(int i=1;i<=n;i++) {
            if(de2[i]==0) {
               q.push(i);
               if(a[i]==0) r[i]=n;
            } 
        }
        while(q.size()) {
            int u=q.front();q.pop();
            for(int i:g2[u]) {
                int res=r[u]-1;
                if(res<1) {ok=0;return;};
                if(a[i]!=0&&a[i]>res) {ok=0;return;}
                else if(a[i]!=0) r[i]=a[i];
                else r[i]=min(r[i],res);
                de2[i]--;
                if(de2[i]==0) q.push(i);
            }
        }
    };
    
    topo1();
    topo2();
    vector<array<int,3>>g(n+1);
    vector<int>ans(n+1);
    for(int i=1;i<=n;i++) {
        g[i]={l[i],r[i],i};
        if(r[i]<l[i]) ok=0;
    }
    sort(g.begin()+1,g.end());
    priority_queue<pair<int,int>>q;
    int lt=1;
    for(int i=1;i<=n;i++) {
        while(lt<=n) {
            if(g[lt][0]==i) q.push({-g[lt][1],g[lt][2]});
            else break;
            lt++;
        }
        if(q.size()==0) {ok=0;break;}
        auto [val,id]=q.top();q.pop();
        if(i<=-val) ans[id]=i;
        else ok=0;
    }
    if(!ok) {puts("-1");return;}
    for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
    puts("");
}

signed main()
{
    int t=read();
    while(t--) solve();
    return 0;
}

K. Barrel Theory

题目大意：构造长度为 n n n的正整数序列使得和为 m m m，并且序列的异或和要严格小于最小值。
题解：首先可以看出， n = 1 n=1 n=1时，一定无解。
然后， n = 2 n=2 n=2时，如果 m + 1 2 \frac{m+1}2 2m+1​和 m 2 \frac{m}2 2m​不能满足条件，就一定无解，否则就可以这样构造。
对于 n = 3 n=3 n=3的情况可以打表发现其中如果 m > 19 m>19 m>19就一定有解，并且其中的某一个数字不会超过7，因此我们就可以对于 n = 3 n=3 n=3的情况，暴力枚举所有可能即可。
对于 n > 3 n>3 n>3的情况，可以分成以下四类：

  1. n n n为偶数， m m m为偶数：
    构造(1,1,1,1……),(m-n+2)/2,(m-n+2)/2。
  2. n n n为奇数， m m m为偶数（需要满足 m > n + 2 m>n+2 m>n+2）:
    构造(1,2,3),(1,1,1,1……),(m-n-1)/2,(m-n-1)/2
  3. n n n为偶数， m m m为奇数（需要满足 m > 2 n m>2n m>2n）:
    构造(2,3),(2,2,2,2……),(m-2n+3)/2,(m-2n+3)/2
  4. n n n为奇数， m m m为奇数（需要满足 m > 2 n + 6 m>2n+6 m>2n+6）:
    构造(4,7,2),(2,2,2,2……),(m-2n-3)/2,(m-2n-3)/2
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#define time chrono::system_clock::now().time_since_epoch().count()
#include<ext/pb_ds/tree_policy.hpp>
#define clean(x) memset(x,0,sizeof(x))
#define fil(x,n) fill(x,x+1+n,0)
#define inf 2000000009
#define maxn 2000005
using namespace std;
using namespace __gnu_pbds;
mt19937_64 rnd(time);
cc_hash_table<int,int>mp;

int read() {
    int x=1,res=0;
    char c=getchar();
    while(c<'0'||c>'9') {
        if(c=='-') x=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9') {
        res=res*10+(c-'0');
        c=getchar();
    }
    return res*x;
}

vector<int>ans;
int check(int n,int m) {
    int x,y,pd=0;
    if(n==2) { //n=2
        x=(m+1)/2;
        y=m/2;
        if((x^y)<min(x,y)) pd=1;
        ans.push_back(x);
        ans.push_back(y);
    } 
    else if(n==3) { //n=3
        for(int x=1;x<=m/3;x++) {
            for(int y=x;y<=(m-x)/2;y++) {
                int z=m-x-y;
                if((x^y^z)<min({x,y,z})) {
                    pd=1;
                    ans.push_back(x);
                    ans.push_back(y);
                    ans.push_back(z);
                    break;
                }
            }
            if(pd) break;
        }
    }
    else { //n>3
        pd=1;
        if(n%2==0&&m%2==0) {
            for(int i=1;i<=n-2;i++) ans.push_back(1);
            ans.push_back((m-n+2)/2);
            ans.push_back((m-n+2)/2);
        }
        else if(n%2==0&&m%2==1) {
            for(int i=2;i<=3;i++) ans.push_back(i);
            for(int i=1;i<=n-4;i++) ans.push_back(2);
            for(int i=1;i<=2;i++) ans.push_back((m-2*n+3)/2);
        }
        else if(n%2==1&&m%2==0) {
            for(int i=1;i<=3;i++) ans.push_back(i);
            for(int i=1;i<=n-5;i++) ans.push_back(1);
            ans.push_back((m-n-1)/2);
            ans.push_back((m-n-1)/2);
        }
        else if(n%2==1&&m%2==1) {
            for(int i=1;i<=n-4;i++) ans.push_back(2);
            ans.push_back(4);ans.push_back(7);
            ans.push_back((m-2*n-3)/2);
            ans.push_back((m-2*n-3)/2);
        }
    }
    return pd;
}

void solve() {
    ans.clear();
    int n=read(),m=read();
    if(n==1||m==n+1) {puts("NO");}
    else if((m<2*n&&m%2==1)||(n%2==1&&m<2*n+7&&m%2==1)) {puts("NO");}
    else {
        if(!check(n,m)) puts("NO");
        else {
            cout<<"YES\n";
            for(int i:ans) cout<<i<<" ";
            puts("");
        }
    }
}

signed main()
{
    int t=read();
    while(t--) solve();
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/181008.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

WhiteHole Base beta版本正式发布！

WhiteHole Base beta版本正式发布！

体验 当前版本为基础测试版本&#xff0c;测试效果可以前往演示视频查看&#xff1a;https://www.bilibili.com/video/BV18Y411D7sA/?spm_id_from333.999.0.0&vd_source641e71dfd1a118fb834c4a5d156688d5 在线体验地址为&#xff1a; http://47.100.239.95 数据将保存~ …
阅读更多...
BGP基础实验

BGP基础实验

1.先配置好IP和环回 [R1]interface GigabitEthernet 0/0/0 [R1-GigabitEthernet0/0/0]ip add 12.1.1.1 24 [R1-GigabitEthernet0/0/0]int l 0 [R1-LoopBack0]ip add 1.1.1.1 24 其他同理 2.在R2&#xff0c;R3&#xff0c;R4上配置OSPF ospf 1 area 0.0.0.0 network 3.3.3.3…
阅读更多...
线段树（原理，模板）

线段树（原理，模板）

文章目录线段树线段树代码(单点修改、区间查询)懒惰标记与区间修改树状数组与区间修改线段树 线段树是用来维护 区间信息 的数据结构 它可以在 O(log⁡n)O(\log n)O(logn) 的时间复杂度内实现单点修改、区间修改、区间查询&#xff08;区间求和&#xff0c;求区间最大值&…
阅读更多...
Reasoning Through Memorization: Nearest Neighbor Knowledge Graph Embeddings论文阅读

Reasoning Through Memorization: Nearest Neighbor Knowledge Graph Embeddings论文阅读

研究问题 将基于记忆的方法与预训练语言模型相结合&#xff0c;以完成知识图谱补全任务 背景动机 传统模型无法处理未见实体记忆增强神经网络的相关进展&#xff0c;即在传统的计算模块之外添加单独的记忆存储模块 模型方法 首先使用预训练语言模型构建实体的知识库&#…
阅读更多...
计算机网络第一章 计算机网络与因特网

计算机网络第一章 计算机网络与因特网

1.0 目录[TOC]1.1 什么是Internet&#xff1f;1.1.1 最细微&#xff1a;图&#xff08;Graph&#xff09;Internet由结点Node和边Edge组成结点Node分为主机结点和交换结点边Edge分为接入网链路Access和主干链路Backbone结构图如下&#xff1a;1.1.2 网络的网络&#xff08;Netw…
阅读更多...
【Python】数值计算基础

【Python】数值计算基础

note scipy和numpy库可以便捷地进行科学计算&#xff0c;如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等。 文章目录note一、多项式基础1. 1 多项式表示和拟合1.2 多项式插值二、微积分计算2.1 数值积分2.2 符号积分三、矩阵运算3.1 线性方程组的求解3.2 矩…
阅读更多...
PHP代码审计之MVC与ThinkPHP简介

PHP代码审计之MVC与ThinkPHP简介

今天继续给大家介绍渗透测试相关知识&#xff0c;本文主要内容是PHP代码审计之MVC与ThinkPHP简介。 免责声明&#xff1a; 本文所介绍的内容仅做学习交流使用&#xff0c;严禁利用文中技术进行非法行为&#xff0c;否则造成一切严重后果自负&#xff01; 再次强调&#xff1a;严…
阅读更多...
文化向技术投降

文化向技术投降

《技术垄断:文化向技术投降》泼斯曼 技术发展三个阶段 1&#xff0c;工具使用文化 2&#xff0c;技术统治文化 3&#xff0c;技术垄断文化 趣讲大白话&#xff1a;科技是一把双刃剑 泛滥的信息已经把人给弄懵了 *********** 广义上来讲&#xff0c;公司是技术公司 才有可能有更…
阅读更多...
Windows压缩工具 “ Bandizip 与 7-zip ”

Windows压缩工具 “ Bandizip 与 7-zip ”

前言 &#x1f4dc;“作者 久绊A” 专注记录自己所整理的Java、web、sql等&#xff0c;IT技术干货、学习经验、面试资料、刷题记录&#xff0c;以及遇到的问题和解决方案&#xff0c;记录自己成长的点滴 目录 前言 一、什么是压缩 二、Bandizip的简介 1、大概介绍 2、详细…
阅读更多...
Acwing---1238.日志统计

Acwing---1238.日志统计

日志统计1.题目2.基本思想3.代码实现1.题目 小明维护着一个程序员论坛。现在他收集了一份”点赞”日志&#xff0c;日志共有 NNN 行。 其中每一行的格式是&#xff1a; ts id 表示在 tststs 时刻编号 ididid 的帖子收到一个”赞”。 现在小明想统计有哪些帖子曾经是”热帖…
阅读更多...
一起自学SLAM算法：9.3 SVO算法

一起自学SLAM算法：9.3 SVO算法

连载文章&#xff0c;长期更新&#xff0c;欢迎关注&#xff1a; 下面将从原理分析、源码解读和安装与运行这3个方面展开讲解SVO算法。 9.3.1 SVO原理分析 前面已经说过&#xff0c;SVO算法是半直接法的典型代表。因此在下面的分析中&#xff0c;首先介绍一下半直接法的基本原…
阅读更多...
网络攻防中监控某个IP的流量和数据分析

网络攻防中监控某个IP的流量和数据分析

网络攻防中监控某个IP的流量和数据分析。 Windows 可以使用 tcpview 工具监控某个IP的流量信息&#xff0c;Linux 可以使用iftop 工具。 新版本的 tcpview 带过滤功能&#xff0c;可以对 IP 进行过滤。最后两列显示的是对应程序发送和接收的字节数。 tcpview 工具下载地址&am…
阅读更多...
【Quicker】您的指尖工具箱

【Quicker】您的指尖工具箱

在日常学习和工作中我们常常用到各种各样的小工具&#xff0c;比如&#xff1a;截图并编辑、取色、文字识别、公式识别等等.   倘若这每一项功能都下载一个程序&#xff0c;则会显得非常冗杂。因此&#xff0c;用一个工具箱将这些功能集合起来&#xff0c;则是一个不错的解决…
阅读更多...
机器自动翻译古文拼音 - 十大宋词 - 满江红 怒发冲冠 南宋·岳飞

机器自动翻译古文拼音 - 十大宋词 - 满江红 怒发冲冠 南宋·岳飞

满江红 怒发冲冠 南宋岳飞 怒发冲冠&#xff0c;凭栏处&#xff0c;潇潇雨歇。 抬望眼&#xff0c;仰天长啸&#xff0c;壮怀激烈。 三十功名尘与土&#xff0c;八千里路云和月。 莫等闲&#xff0c;白了少年头&#xff0c;空悲切。 靖康耻&#xff0c;犹未雪。臣子恨&#x…
阅读更多...
点云 3D 分割 - RangeNet++（IROS 2019）

点云 3D 分割 - RangeNet++（IROS 2019）

点云 3D 分割 - RangeNet&#xff08;IROS 2019&#xff09;摘要1. 引言2. 相关工作3. 我们的方法A. 距离图像点云代理表示B. 完全卷积语义分割C. 基于距离图像的点云重建D. 高效点云后处理4. 实验评价A. RangeNet相对于最新技术的性能B. 消融研究C. 后处理影响D. 运行时5. 结论…
阅读更多...
JavaWeb | 预编译SQL及PreparedStatement讲解

JavaWeb | 预编译SQL及PreparedStatement讲解

本专栏主要是记录学习完JavaSE后学习JavaWeb部分的一些知识点总结以及遇到的一些问题等&#xff0c;如果刚开始学习Java的小伙伴可以点击下方连接查看专栏 本专栏地址&#xff1a;&#x1f525;JDBC Java入门篇&#xff1a; &#x1f525;Java基础学习篇 Java进阶学习篇&#x…
阅读更多...
JavaSE总结

JavaSE总结

JavaSE目录初识JavaJava由来main 方法介绍Java程序的运行数据类型和变量数据类型基本数据类型引用数据类型运算符算术运算符关系运算符逻辑运算符移位运算逻辑控制方法方法的重载与重写关于递归数组二维数组类和对象成员变量成员方法对象this 关键字构造方法封装代码块内部类非…
阅读更多...
ext文件系统

ext文件系统

Ext文件系统 1.文件目录 1.1 文件控制块FCB 文件系统通过文件控制块&#xff08;File Control Blcok&#xff09;来维护文件结构&#xff0c;FCB包含有关文件的信息&#xff0c;包括所有者、权限、文件内容的位置等文件目录用于组织文件&#xff0c;每个目录项对应一个FCB文…
阅读更多...
（考研湖科大教书匠计算机网络）第三章数据链路层-第三节：差错控制

（考研湖科大教书匠计算机网络）第三章数据链路层-第三节：差错控制

专栏目录首页&#xff1a;【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一&#xff1a;检错编码&#xff08;1&#xff09;奇偶校验码&#xff08;2&#xff09;循环冗余检验码&#xff08;CRC&#xff09;二&#xff1a;纠错编码&#xff08;海明校验码&#xff0…
阅读更多...
Opencv调参神器——trackBar控件

Opencv调参神器——trackBar控件

Opencv调参神器——trackBar控件 调参需求介绍trackBar控件介绍trackBar控件使用函数案例一：trackBar控件调整图片颜色案例二：trackBar控件调整Canny算子参数案例三：trackBar控件调整图像融合参数trackBar控件总结调参需求介绍 想要学好计算机视觉，有一个库必不可少，那就…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023