星期一：
abc356 D atc传送门
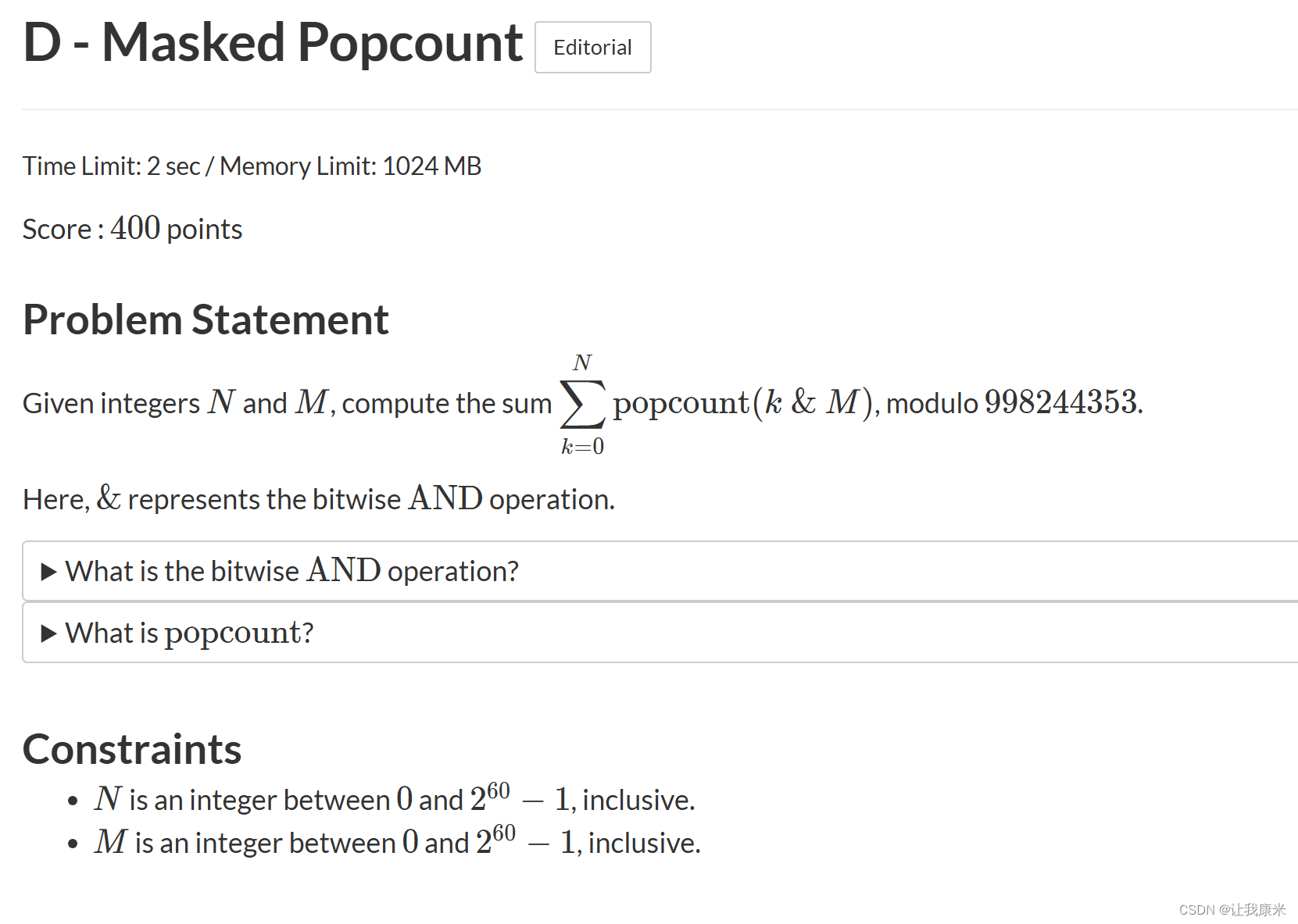
思路：按位与操作，M的非零位对答案一定没有贡献，对M为1的位，考虑有多少k此位也为1
按位枚举，m此位为0跳过，例如n为110 0 10，枚举到第2位(从0开始，考虑多少种情况此位为1，此时n此位为0，左边的数为110，右边为10，先考虑左边的取值，若小于110，则后面任意取值，有 2^2 种情况(指数为右边数长度，若等于110，则若中间位为1，有10种情况，若为0，则无贡献
代码如下：
const int mod=998244353;
ll n;
void solve(){
ll m; cin >> n >> m;
ll ans=0;
for(int i=0;i<60;i++){
if(!((m>>i)&1)) continue;
ll l=n>>i+1;
ll r=n%(1ll<<i);
ans+=l*(1ll<<i)%mod+(n>>i&1)*(r+1),ans%=mod;
}
cout << ans;
}百度之星2023 新的阶乘 mtj传送门
线性筛好题，暴力分解质因数会t
思路：做这题得先了解线性筛，为什么每个数只会被筛一次，每个数是被其最小质因子筛掉的， 一个数如果是合数，应该把指数加在自己的因子上，例如，12^5 = 2^5 * 6^5，6^5 = 2^5 * 3^5，像酱紫往下传，所以可以从大到小枚举，在线性筛的时候顺便存下每个数的最小质因子
代码如下：
const int N=1e7+10,M=210;
ll n;
int p[N],idx;
bool vi[N];
int minpf[N];
ll v[N];
void getp(int x){
for(int i=2;i<=x;i++){
if(!vi[i]) p[++idx]=i,minpf[i]=i;
for(int j=1;1ll*i*p[j]<=x;j++){
vi[i*p[j]]=1;
minpf[i*p[j]]=p[j];
if(i%p[j]==0) break;
}
}
}
void solve(){
cin >> n;
getp(n);
for(int i=2;i<=n;i++) v[i]=n+1-i; //赋上指数初值
map<int,ll>mp;
int ma=0;
for(int i=n;i>1;i--){
if(i==minpf[i]) mp[i]=v[i],ma=max(i,ma); //为质数,记录答案
else{
v[minpf[i]]+=v[i];
v[i/minpf[i]]+=v[i]; //为合数,下传指数
ma=max({minpf[i],i/minpf[i],ma});
}
}
cout << "f(" << n << ")=";
for(auto [a,b]:mp){
if(a==ma){
if(b==1) cout << a;
else cout << a << "^" << b;
}else{
if(b==1) cout << a << "*";
else cout << a << "^" << b << "*";
}
}
}学了下迭代写法的快速幂，感觉比递归好写点：
ll qpow(int a,int n){
ll res=1;
while(n){
if(n&1) res=res*a%mod;
a=a*a%mod;
n>>=1;
}
return res;
}cf 148 D 抓老鼠 概率dp cf传送门
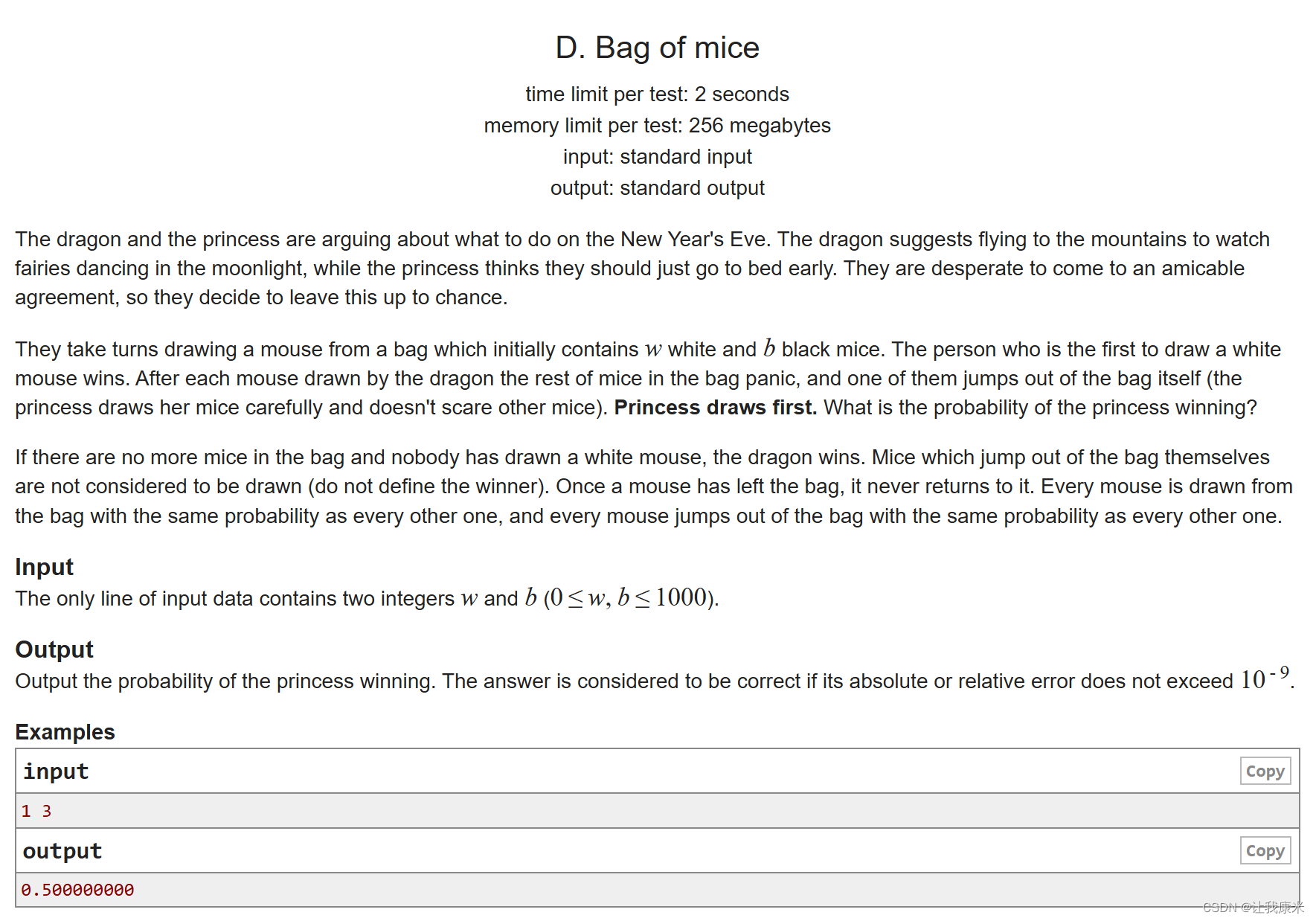题意：俩人轮流从袋子里抓老鼠，w只白鼠，b只黑鼠，谁先抓到白鼠谁赢，问先手赢的概率
思路：dp【i】【j】表示袋子有 i只白鼠，j只黑鼠先手赢的概率，初始状态 dp【i】【0】为1， dp【0】【i】为0，答案为 dp【w】【b】
分类讨论情况来转移：
先手白，直接赢
先手黑，后手白，输，对答案无贡献
先手黑，后手黑，跑出一只黑 / 白，从 dp【i】【j-3】和 dp【i-1】【j-2】转移
代码如下：
int w,b;
double dp[1010][1010];
void solve(){
cout << fixed << setprecision(11);
cin >> w >> b;
for(int i=1;i<=w;i++) dp[i][0]=1;
for(int i=1;i<=b;i++) dp[0][i]=0;
for(int i=1;i<=w;i++){
for(int j=1;j<=b;j++){
dp[i][j]+=1.0*i/(i+j);
if(i>=1 && j>=2) dp[i][j]+=1.0*j/(i+j)*(j-1)/(i+j-1)*i/(i+j-2)*dp[i-1][j-2];
if(j>=3) dp[i][j]+=1.0*j/(i+j)*(j-1)/(i+j-1)*(j-2)/(i+j-2)*dp[i][j-3];
}
}
cout << dp[w][b];
}poj 3071 球队淘汰赛 vj传送门
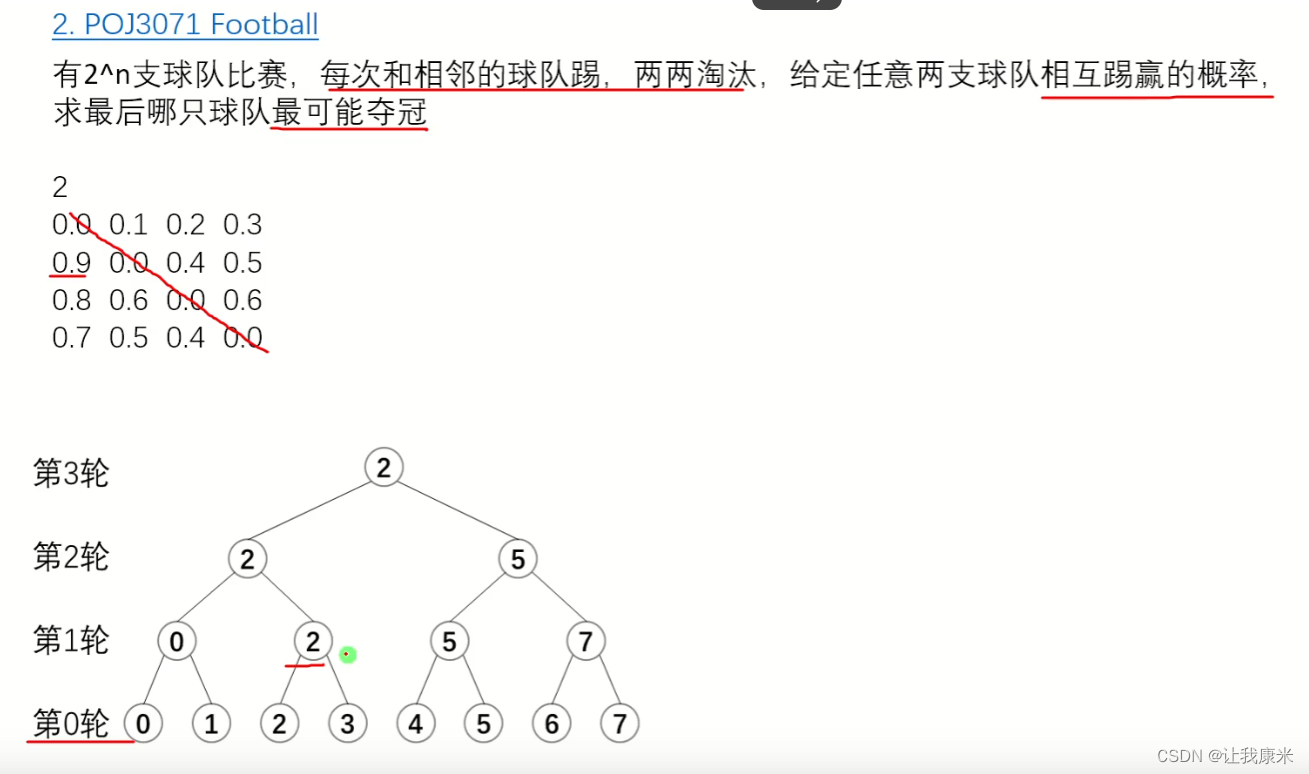
注意原题的提交不支持万能头, 以及可能有奇奇怪怪的编译报错
思路 : dp【i】【j】表示第 i队活到第 j轮的概率
这题唯一比较麻烦的点就是，如何找出每一轮是哪些队pk
代码如下:
ll n;
double dp[132][11];
double a[132][132];
void solve(){
while(cin >> n && n!=-1){
for(int i=1;i<=1<<n;i++){
for(int j=1;j<=1<<n;j++)
cin >> a[i][j];
}
for(int i=1;i<=1<<n;i++)
for(int j=1;j<=n;j++) dp[i][j]=0;
for(int i=1;i<=1<<n;i++) dp[i][0]=1; //初始化
for(int rd=1;rd<=n;rd++){ //枚举轮数
int len=1<<rd;
for(int l=1;l+len-1<=1<<n;l+=len){
int r=l+len-1;
int mid=l+r>>1;
for(int i=l;i<=mid;i++){
for(int j=mid+1;j<=r;j++){ //i和j在第rd轮比赛
dp[i][rd]+=dp[i][rd-1]*dp[j][rd-1]*a[i][j];
dp[j][rd]+=dp[j][rd-1]*dp[i][rd-1]*a[j][i];
}
}
}
}
int ans=0;double cmp=0;
for(int i=1;i<=1<<n;i++)
if(dp[i][n]>cmp){cmp=dp[i][n],ans=i;}
cout << ans << "\n";
}
}晚上cf round950 div3好不容易出了5题，c被人用卡unordered_map的数据hack掉了，无言
星期二：
期望dp 换教室 洛谷传送门
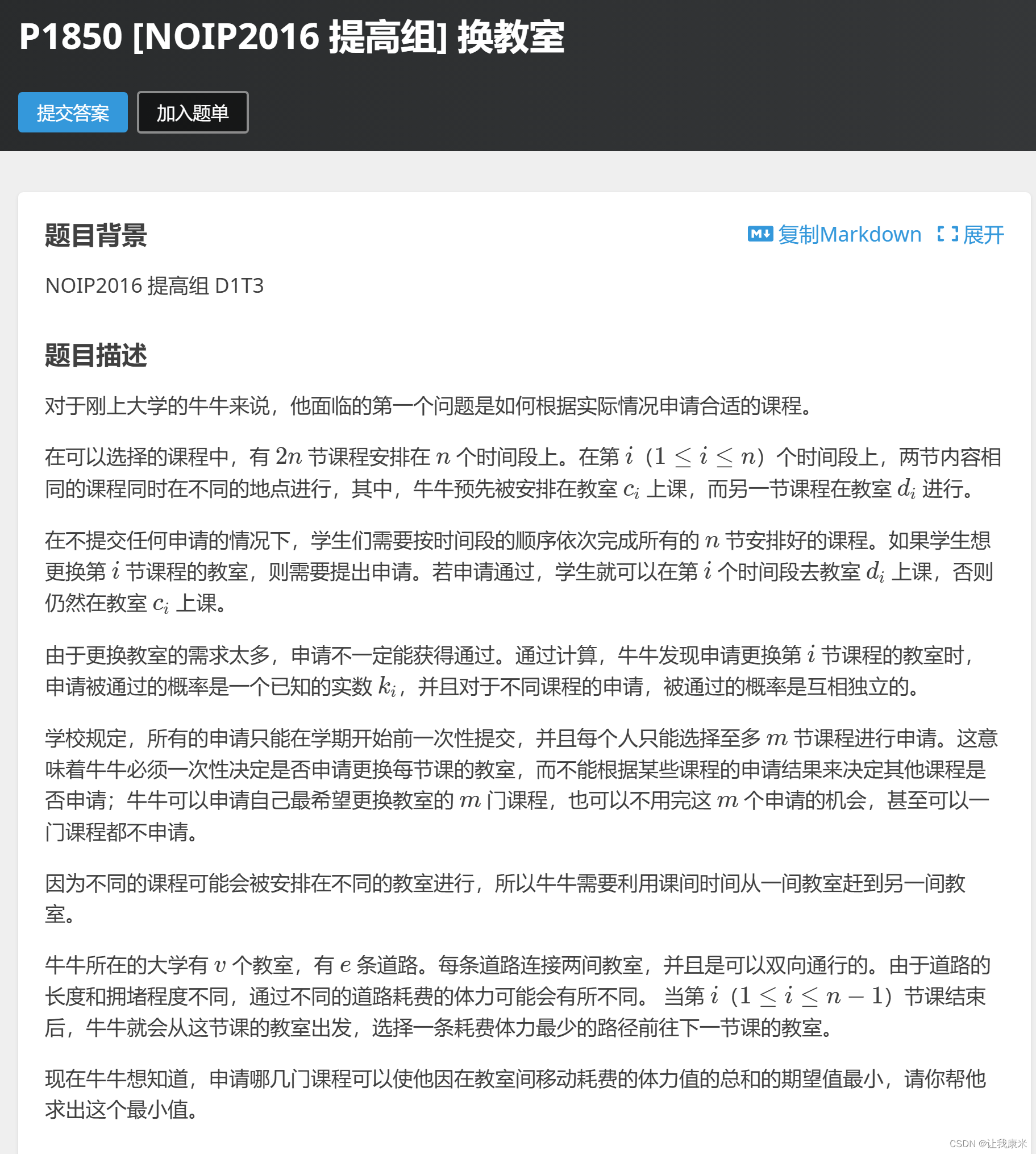
思路：dp【i】【j】【0 / 1】表示到第 i个时段，申请了 j次，这次 没有/有 申请的期望路程
转移比较麻烦
需要将dp数组初始化为极大值，否则转移会出问题
代码如下：
ll n;
int m,v,e;
int c[2020],d[2020];
double p[2020];
int dis[330][330];
double dp[2020][2020][2];
void solve(){
cin >> n >> m >> v >> e;
for(int i=1;i<=v;i++)
for(int j=1;j<i;j++) dis[i][j]=dis[j][i]=1e9;
for(int i=1;i<=n;i++) cin >> c[i];
for(int i=1;i<=n;i++) cin >> d[i];
for(int i=1;i<=n;i++) cin >> p[i];
for(int i=1;i<=e;i++){
int a,b,w; cin >> a >> b >> w;
dis[a][b]=dis[b][a]=min(dis[a][b],w);
}
for(int k=1;k<=v;k++){
for(int i=1;i<=v;i++)
for(int j=1;j<=v;j++)
dis[i][j]=min(dis[i][k]+dis[k][j],dis[i][j]);
}
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++) dp[i][j][0]=dp[i][j][1]=1e9;
dp[1][0][0]=0,dp[1][1][1]=0;
for(int i=2;i<=n;i++){
for(int j=0;j<=min(i,m);j++){
dp[i][j][0]=min(dp[i-1][j][0]
+dis[c[i]][c[i-1]],
dp[i-1][j][1]
+p[i-1]*dis[c[i]][d[i-1]]
+(1-p[i-1])*dis[c[i]][c[i-1]]);
if(j>0)
dp[i][j][1]=min(dp[i-1][j-1][0]
+p[i]*dis[d[i]][c[i-1]]
+(1-p[i])*dis[c[i]][c[i-1]],
dp[i-1][j-1][1]
+p[i]*p[i-1]*dis[d[i]][d[i-1]]
+(1-p[i])*p[i-1]*dis[c[i]][d[i-1]]
+p[i]*(1-p[i-1])*dis[d[i]][c[i-1]]
+(1-p[i])*(1-p[i-1])*dis[c[i]][c[i-1]]);
}
}
double ans=1e9;
for(int i=0;i<=m;i++)
ans=min({dp[n][i][0],dp[n][i][1],ans});
cout << fixed << setprecision(2) << ans << "\n";
}星期三：
补24东北 L cf传送门
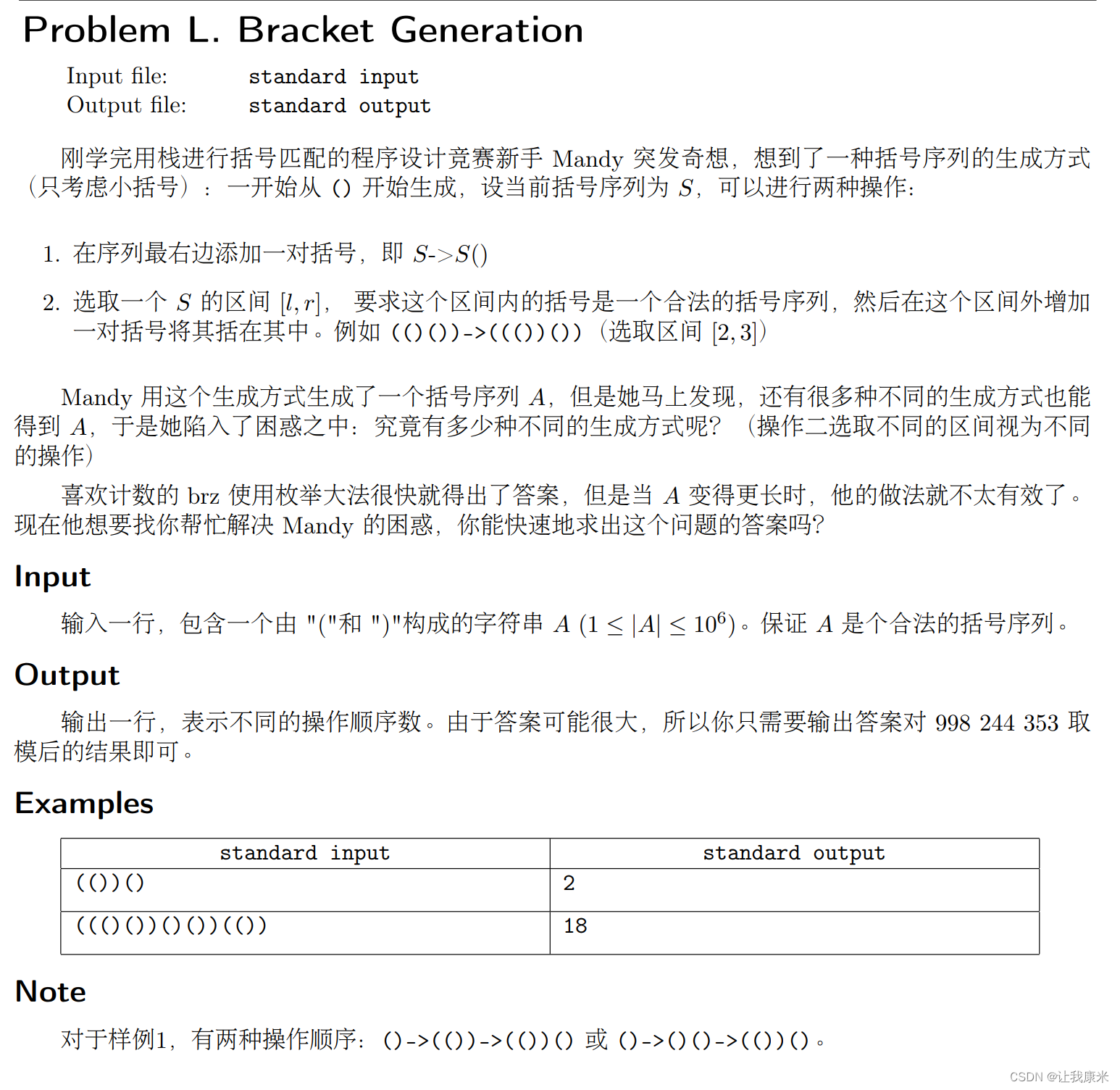
思路：我不到啊
代码如下：
ll n;
void solve(){
string s; cin >> s;
n=s.size(); s=" "+s;
stack<int>sk;
vector<int>ve;
for(int i=1;i<=n;i++){
if(s[i]=='(') sk.push(i);
else{
if(sk.top()==i-1) ve.push_back(1);
else ve.push_back(2);
sk.pop();
}
}
reverse(ve.begin(),ve.end());
ll ans=1,cnt=0;
for(auto i:ve){
cnt++;
if(i==2) ans=ans*cnt%mod;
}
cout << ans;
}补20届东南校赛 J cf传送门
思路：dp【i】【j】表示考虑到第 i个，分成 j段的最低子段值
s【i】【j】表示在（ i , j ]中有多少子段和为x，进行 n*n*k的枚举转移答案
其实转移并不难，赛时没出可能是预处理的思路出错了，且不熟悉 n^2的转移？
代码如下：
ll n;
ll a[3030];
int s[3030][3030],dp[3030][22];
void solve(){
int k,x; cin >> n >> k >> x;
for(int i=1;i<=n;i++) cin >> a[i],a[i]+=a[i-1];
for(int i=0;i<n;i++){
unordered_map<int,int>mp;
int cnt=0;
mp[a[i]]=1;
for(int j=i+1;j<=n;j++){
if(mp[a[j]-x]) cnt+=mp[a[j]-x];
mp[a[j]]++;
s[i][j]=cnt;
}
}
memset(dp,0x3f,sizeof dp);
dp[0][0]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=k;j++)
for(int y=0;y<i;y++)
dp[i][j]=min(dp[y][j-1]+s[y][i],dp[i][j]);
}
cout << dp[n][k];
}星期四：
cf 期望dp 魔镜 cf传送门
思路：dp【i】表示从头问，问到第 i个镜子且漂亮的期望天数
转移为：dp【i】= pi/100* ( dp【i-1】+1）+ （ 1 - pi/100）*（ dp【i】+1）
上述转移错误，应为：dp【i】= dp【i-1】+ pi/100 + （ 1 - pi/100）*（ dp【i】+1）
到第 i面镜子首先需要dp【i-1】的天数，有 pi/100的概率漂亮，即比 dp【i-1】多1天，有（1-pi/100）的概率不漂亮，那么除了不漂亮的这一天，还要再花 dp【i】天
化简可得递推式，快速幂的a，记得开 ll
代码如下：
const int mod=998244353;
ll n;
ll qpow(ll a,int n){
ll res=1;
while(n){
if(n&1) res=res*a%mod;
a=a*a%mod;
n>>=1;
}
return res;
}
void solve(){
cin >> n;
ll ans=0;
for(int i=1;i<=n;i++){
int p; cin >> p;
ans=(ans+1)*100%mod*qpow(p,mod-2)%mod;
}
cout << ans << "\n";
}百度之星2022 逃离树 mtj传送门
思路：dp【i】表示从 i点开始到逃离树的期望天数，叶子节点的dp值即为0
从叶子节点向根节点逆推，对于一个节点 x 分析有哪些情况
第一种情况，去到叶子节点 i，叶子节点逃离的期望天数已知，为dp【i】，dp【x】即dp【i】+1，那么贡献就是 去到 i的概率*（dp【i】+1），累加上所有叶子节点即可
第二种情况，停留一天，dp【x】即为 dp【x】+1，需要注意的是，这里的转移和魔镜长得很像，但实际意义并不相同，因为魔镜的dp【i】定义为从头开始到 i，而逃离的dp【i】定义为从 i开始。对于这种情况也乘上其概率，加到dp【x】
即得 ，注意化简时别出错
代码如下：
const int N=2e6+10,M=210;
const int mod=998244353;
ll n;
int p[N];
vector<PII>ve[N];
ll dp[N];
ll qpow(ll a,int n){
ll res=1;
while(n){
if(n&1) res=res*a%mod;
a=a*a%mod;
n>>=1;
}
return res;
}
void dfs(int x){
if(ve[x].empty()) return ; //叶子节点可直接返回,当然不返回值也会是0
ll sum=p[x];
for(auto [w,i]:ve[x]){
sum+=w; //先算出分母
dfs(i); //预处理出叶子节点
}
dp[x]=sum*qpow(sum-p[x],mod-2)%mod;
for(auto [w,i]:ve[x])
dp[x]+=w*dp[i]%mod*qpow(sum-p[x],mod-2)%mod,dp[x]%=mod;
}
void solve(){
cin >> n;
for(int i=1;i<=n;i++) cin >> p[i];
for(int i=2;i<=n;i++){
int x,y; cin >> x >> y;
ve[x].push_back({y,i});
}
dfs(1);
cout << dp[1];
}星期五：
百度之星 石碑文 mtj传送门
百度之星挺多求方案数的题还挺有意思的
思路：dp【i】【j】表示考虑到第 i个，j表示目前的shs的状态
转载题解：2023 百度之星 题目解析_百度之星真题-CSDN博客，讲的很清晰
由 i-1求 i好像有点吃力或不可行？从 i往 i+1推比较方便，且网上题解貌似都这么写的
代码如下：
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll dp[N][10];
void solve(){
cin >> n;
dp[0][0]=1;
// for(int i=1;i<=n;i++){
// for(int j=0;j<10;j++){
// if(j==9) dp[i][j]=dp[i-1][j]*26%mod;
// else if(j%3==1){
// dp[i][j]+=dp[i-1][j]; //+s
// dp[i][j]+=dp[i-1][j-1]; //+s
// dp[i][j]%=mod;
// }else if(j%3==2){
// dp[i][j]+=dp[i-1][j-1];
// dp[i][j]%=mod;
// }else{
// dp[i][j]+=dp[i-1][j+1]*24%mod;
// dp[i][j]+=dp[i-1][j-1];
// dp[i][j]+=dp[i-1][j]*25%mod;
// dp[i][j]%=mod;
// }
// }
// }
for(int i=0;i<n;i++){
for(int j=0;j<10;j++){
if(j==9) dp[i+1][j]+=dp[i][j]*26%mod,dp[i+1][j]%=mod; //加任意字母
else if(j%3==1){
dp[i+1][j]+=dp[i][j],dp[i+1][j]%=mod; //加s
dp[i+1][j+1]+=dp[i][j],dp[i+1][j+1]%=mod; //加h
dp[i+1][j-1]+=dp[i][j]*24,dp[i+1][j-1]%=mod; //加除了s,h
}else if(j%3==2){
dp[i+1][j+1]+=dp[i][j],dp[i+1][j+1]%=mod; //加s
dp[i+1][j-2]+=dp[i][j]*25%mod,dp[i+1][j-2]%=mod; //加除了s
}else{
dp[i+1][j+1]+=dp[i][j],dp[i+1][j+1]%=mod; //加s
dp[i+1][j]+=dp[i][j]*25%mod,dp[i+1][j]%=mod; //加除了s
}
}
}
cout << dp[n][9];
}补昨晚cf round951 div2 D cf传送门
思路：正解的实现有点复杂
代码如下：
ll n;
int k;
string s;
bool check(string s){
for(int i=2;i<=k;i++)
if(s[i]!=s[i-1]) return 0;
for(int i=1;i<=n-k;i++)
if(s[i+k]==s[i]) return 0;
return 1;
}
void op(int idx){
reverse(s.begin()+1,s.begin()+idx+1);
string ns=" "+s.substr(idx+1,n-idx)+s.substr(1,idx);
if(check(ns)) cout << idx << "\n";
else cout << "-1\n";
}
void solve(){
cin >> n >> k;
cin >> s; s=" "+s;
int cnt=1;
for(int i=n-1;i;i--){
if(s[i]!=s[i+1]) break;
cnt++;
}
if(cnt>k){cout << "-1\n"; return ;}
if(cnt==k){
if(check(s)){
if(s[1]!=s[n] || n==k) cout << k << "\n";
else cout << k*2 << "\n";
}else{
int idx=n;
for(int i=n-k;i;i--)
if(s[i]==s[i+k]){idx=i; break;}
op(idx);
}
}else{
bool if1=0;
for(int i=1,j;i<=n;i++){
if(s[i]!=s[n]) continue;
j=i;
while(j<n && s[j+1]==s[n]) j++;
if(j-i+1==k-cnt){
op(j);
if1=1;
break;
}else if(j-i+1==2*k-cnt){
op(j-k);
if1=1;
break;
}
i=j;
}
if(!if1) op(n);
}
}周末：
牛客打了第二十届西南科技校赛，被道线段树卡住了。
补 C 线段树 牛客传送门
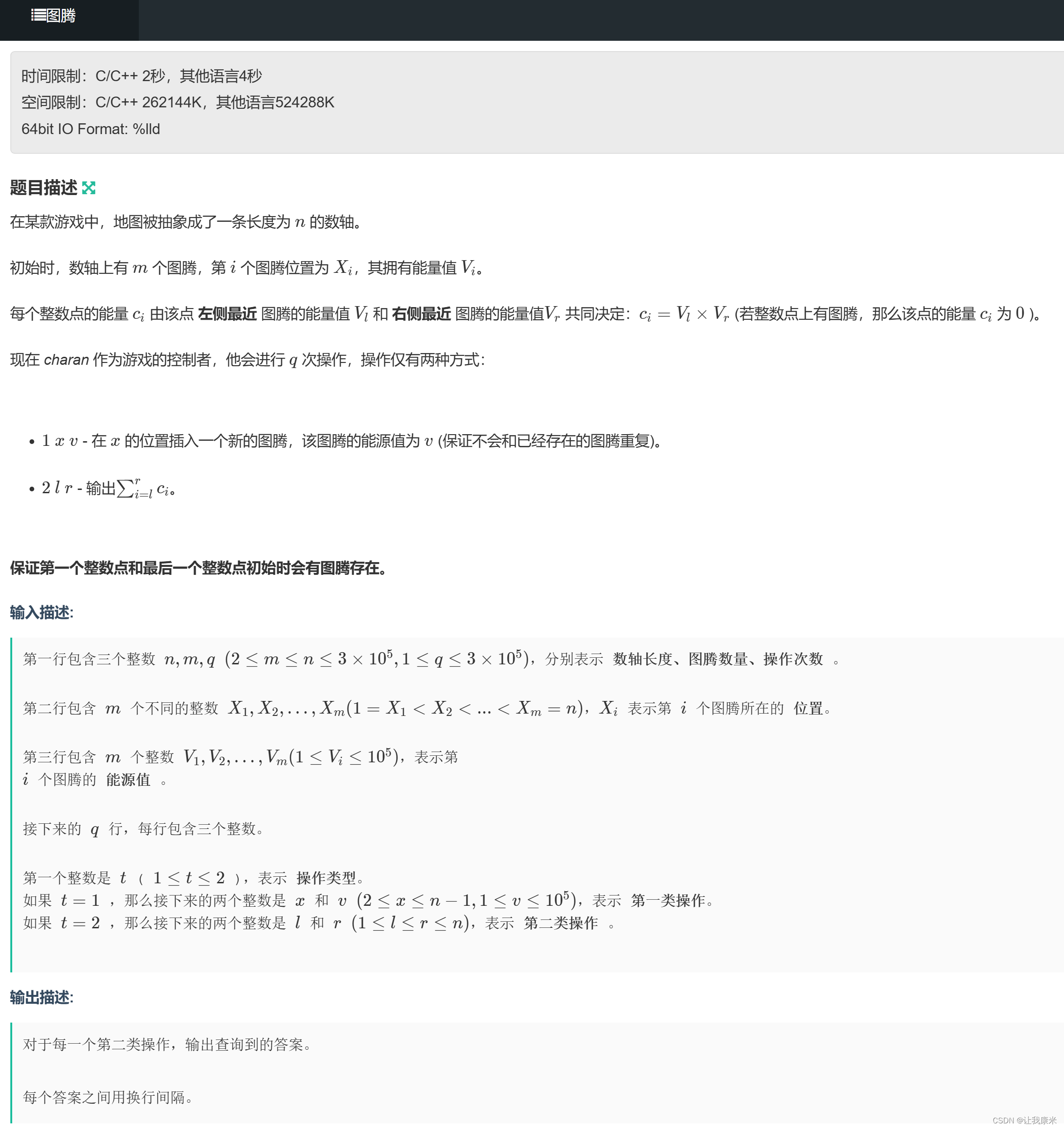
一开始想所有操作都用线段树来做（包括维护图腾，没想出来怎么做
思路：用一个multiset维护图腾的坐标和能量，线段树只需要实现最基本的区修区差就行
代码如下：
const int N=2e6+10,M=210;
ll n;
struct seg_Tree{
#define lc p<<1
#define rc p<<1|1
struct nod{
int l,r;
ll sum,add;
}t[N];
ll ql,qr,qv;
nod merge(nod a,nod b){
nod res;
res.l=a.l,res.r=b.r;
res.sum=a.sum+b.sum;
res.add=0;
return res;
}
void pushup(int p){t[p]=merge(t[lc],t[rc]);}
void pushdn(int p){
if(!t[p].add) return ;
t[lc].sum=(t[lc].r-t[lc].l+1)*t[p].add;
t[rc].sum=(t[rc].r-t[rc].l+1)*t[p].add;
t[lc].add=t[p].add;
t[rc].add=t[p].add;
t[p].add=0;
}
void bd(int p,int l,int r){
t[p]={l,r,0,0};
if(l==r) return ;
int mid=l+r>>1;
bd(lc,l,mid);
bd(rc,mid+1,r);
pushup(p);
}
void update(int p){
if(t[p].l>=ql && t[p].r<=qr){
t[p].sum=1ll*(t[p].r-t[p].l+1)*qv;
t[p].add=qv;
return ;
}
int mid=t[p].l+t[p].r>>1;
pushdn(p);
if(ql<=mid) update(lc);
if(qr>mid) update(rc);
pushup(p);
}
nod query(int p){
if(t[p].l>=ql && t[p].r<=qr) return t[p];
int mid=t[p].l+t[p].r>>1;
pushdn(p);
if(qr<=mid) return query(lc);
if(ql>mid) return query(rc);
return merge(query(lc),query(rc));
}
void updt(int l,int r,ll v){
ql=l,qr=r;
qv=v;
update(1);
}
ll ask(int l,int r){
ql=l,qr=r;
return query(1).sum;
}
}tr;
void solve(){
int m,q; cin >> n >> m >> q;
tr.bd(1,1,n);
vector<int>ve;
ve.push_back(0);
for(int i=1;i<=m;i++){
int p; cin >> p;
ve.push_back(p);
}
multiset<PII>mt;
for(int i=1;i<=m;i++){
int v; cin >> v;
mt.insert({ve[i],v});
}
for(multiset<PII>::iterator it=mt.begin();it!=mt.end();it++){
auto tt=next(it);
if(tt==mt.end()) break;
int p1=it->first,v1=it->second;
int p2=tt->first,v2=tt->second;
if(p1==p2-1) continue;
tr.updt(p1+1,p2-1,1ll*v1*v2);
}
while(q--){
int op; cin >> op;
if(op==1){
int x,v; cin >> x >> v;
tr.updt(x,x,0);
auto pv1=*(--mt.lower_bound({x,0}));
auto pv2=*(mt.upper_bound({x,0}));
if(pv1.first<x-1) tr.updt(pv1.first+1,x-1,1ll*pv1.second*v);
if(x<pv2.first-1) tr.updt(x+1,pv2.first-1,1ll*pv2.second*v);
mt.insert({x,v});
}else{
int l,r; cin >> l >> r;
cout << tr.ask(l,r) << "\n";
}
}
}
