素数的无穷大——欧几里得的证明
文章目录
- 一、说明
- 二、欧几里得证据
- 三、哥德巴赫对素数无穷性的证明(1730)
- 四、Fürstenberg 对素数无穷性的证明(1955)
- 五、库默尔对欧几里得证明的重述
一、说明
众所周知,素数是无限多的。然而,两千多年前的情况并非如此。当时,数学还处于非常初级的阶段,尚未得到发展。自然,质数是一个有吸引力的探索前沿。要处理素数,首先要了解它最基本的性质——有多少个素数?
欧几里得可能是第一个证明有无穷多个素数的人。即使在 2000 年后,它仍然是一个优秀的推理模型。下面我们遵循 Ribenboim 对欧几里得证明的陈述 [ Ribenboim95 ,第 3 页],请参阅“有无穷多个素数”页面以了解其他几个证明。
二、欧几里得证据
即使在今天,欧几里得的证明仍然是数学推理和美的极好展示。他的证明首先考虑了任何有限的素数集:
{ p 1 , p 2 , p 3 , . . . p n } \{p_1,p_2,p_3,...p_n \} {p1,p2,p3,...pn}
然后,欧几里得的方法涉及证明至少存在一个素数,使其不属于该集合。我们设 P 是该集合成员的乘积,即:
P
=
p
1
∗
p
2
∗
p
3
,
.
.
.
∗
p
n
P=p_1*p_2*p_3,...*p_n
P=p1∗p2∗p3,...∗pn
我们定义 Q = P + 1。
接下来,我们继续通过穷竭来完成这个证明。需要注意的是,这个证明的推论是算术的基本定理:每个大于 1 的数字都可以表示为质因数的唯一乘积。
欧几里得利用了这个定理,产生了两种情况:
- Q 是素数。
- Q 是复合的(不是素数)。
他首先单独考虑每个案例。
-
在 Q 是素数的情况下,Q 不属于我们开始的有限素数集(因为 Q > P),因此,有一个素数不是该集合的成员, 因此,素数是无限的。
-
在 Q 是复合的情况下,Q 具有唯一的质因式分解,并且一些质数 r 除以 Q。如果这个质因数 r 属于我们开始的有限集合,那么它将除以 P,因为 P 是集合中素数的乘积。但 r 还将 Q = P + 1 除以构造。现在,如果 r 除以 Q 和 r 除以 P,那么它也必须除以两者之间的差值。也就是说,它还必须除以 1。由于没有素数除以 1,因此 r 是不属于该集合的素数。
在这两种情况下,素数都存在于有限集之外。这表明,对于每个有限的素数集,至少存在一个不在列表中的素数,从而证明了素数的无穷大。
欧几里得证明的变体
欧几里得证明的变体遵循类似的推理,但涉及阶乘的使用。数字 x 的阶乘,用 x! 表示,定义为所有小于或等于自身的自然数的乘积:
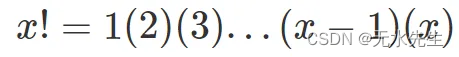
在这个版本的证明中,我们首先注意到 x! 可被从 2 到 x 的每个整数整除,包括 2 和 x。 因此,x! + 1 不能被任何小于 x 的正整数整除。因此,x! + 1 要么是素数,要么可以被大于 x 的素数整除。 在任何情况下,对于每个正整数 x,都有一个大于 x 的素数。有了这个,我们可以得出结论,有无限数量的素数。
欧几里得可能是第一个证明有无穷多个素数的人,但他的证明后来被许多人效仿。下面我们给出哥德巴赫使用费马数(写于 1730 年 7 月写给欧拉的一封信中)的巧妙证明,以及一些变体。请参阅“有无穷多个素数”页面,了解更多证明。
三、哥德巴赫对素数无穷性的证明(1730)
https://t5k.org/notes/proofs/infinite/goldbach.html
首先我们需要一个引理。
引理。
费马数
F
n
=
2
2
n
+
1
F_n =2^{2^n}+1
Fn=22n+1是两两互质的。
证明。
通过归纳法很容易证明
F
m
−
2
=
F
0.
F
1.....
F
m
−
1
F m -2 = F 0 . F 1 . ... . F m -1
Fm−2=F0.F1.....Fm−1。这意味着如果d能整除 F n和 F m(其中n < m),那么d也能整除 F m -2 ;因此d能整除 2 。但每个费马数都是奇数,因此d为 1。
现在我们可以证明这个定理:
定理。
素数有无数个。
证明。
为每个费马数 F n选取一个素数因子 p n。根据引理,我们知道这些素数都是不同的,表明素数有无穷多个。
请注意,任何两两互质的序列都可以用于此证明。这种类型的序列很容易构造。例如,选择互质整数a和b,然后按如下方式定义 a n 。
a 1 = a ,
a 2 =a 1 + b ,
a 3 =a 1 a 2 + b ,
a 4 =a 1 a 2 a 3 + b ,
…
这包括费马数(a =1,b =2)和西尔维斯特数列(a =1,b =2):
a 1 =2 且 a n +1 = a n 2 -a n +1。
事实上,证明实际上只需要一个具有成对互质的子序列的序列,例如梅森数。
四、Fürstenberg 对素数无穷性的证明(1955)
https://t5k.org/notes/proofs/infinite/topproof.html
克里斯·考德威尔
欧几里得可能是第一个证明有无穷多个素数的人。此后,人们给出了许多其他证明。也许最奇怪的是 Fürstenberg [ Fürstenberg55 ] 给出的以下拓扑证明。请参阅“有无穷多个素数”页面,了解其他几个证明。
[定理] 素数有无数个。
[证明]
以等差数列(从-无穷到+无穷)为基础,在整数集上定义一个拓扑。很容易验证这会产生一个拓扑空间。对于每个素数p ,设A p 由p的所有倍数组成。A p是闭集,因为它的补集是所有其他差值为p 的等差数列的并集。现设A为数列A p 的并集 。如果素数的数量是有限的,则A是闭集的有限并集,因此是封闭的。但除 -1 和 1 之外的所有整数都是某个素数的倍数,因此A的补集为 {-1, 1},显然不是开集。这表明A不是有限并集,且素数有无穷多个。
五、库默尔对欧几里得证明的重述
克里斯·考德威尔
欧几里得可能是第一个证明有无穷多个素数的人。即使在 2000 年后,它仍然是一个优秀的推理模型。库默尔给出了这个证明的更优雅的版本,我们在下面给出(遵循 Ribenboim [ Ribenboim95 ,第 4 页])。请参阅“有无穷多个素数”页面,了解其他几个证明。
定理。
素数有无数个。
证明。
假设存在有限多个素数p 1 < p 2 < … < p r。设N = p 1 . p 2 . … . p r。整数N -1 是素数的乘积,它与N有一个共同的素数因子p i;因此,p i能整除N - ( N -1) =1,这是荒谬的!∎
收藏











![[chisel]马上要火的硬件语言,快来了解一下优缺点](https://img-blog.csdnimg.cn/img_convert/f9a9c642e73791d405078c6422c17704.webp?x-oss-process=image/format,png)