一、二维数组介绍

二维数组与一维数组很相似。可以说二维数组是元素为一维数组的数组，也就是一维数组的数组。每个元素可以通过行索引和列索引来访问。

1、二维数组的创建

我们知道，在 C 语言中，二维数组是一个连续的内存块，通常在声明时需要指定列数：

1. 列数必须确定：在编译时，列数必须是确定的，以便编译器能够正确计算每一行的偏移量。
2. 行数可以不确定：行数可以在初始化时由编译器通过初始化的元素个数和列数推断出来。

但是 Java 的二维数组与 C 语言的数组是有很多区别的，我们后面也会讲到。

在 Java 中，二维数组实际上是一维数组的数组，这些子数组在内存上不一定连续。这意味着：

1. 行数必须确定：当你创建一个二维数组时，你需要指定行数。
2. 列数可以不确定：每个子数组的元素个数可以单独分配，因此列数可以不同，甚至可以在之后动态分配。

也就是说你必须指出你要创建的子数组的个数（也就是行数），但是子数组的元素个数（也就是列数）不必指出，因为 Java 是支持二维数组子数组长度不同的。

1）列数确定动态创建

与一维数组一致，二维数组也要先声明一个数组引用变量：

int[][] arr;

然后使用 new 关键字创建一个数组对象，然后将数组对象的引用赋值给这个数组引用变量：

arr = new int[2][3];

这里就创建了一个二行三列的二维数组。

与一维数组一样，这两个操作也可以在一个语句中完成：

int[][] arr = new int[3][4];

这里就创建了一个三行四列的二维数组对象，然后将对象的引用赋值给前面的数组引用变量。

2）列数不确定的动态创建

int[][] arr = new int[3][];

这样就是创建了一个二维数组，二维数组的子数组是三个（也就是二维数组有三行），但是子数组的元素个数不确定（也就是列数不确定）。

在后面我们可以在对这个二维数组的每一个子数组进行单独的动态分配，这时就可以对不同的子数组分配不同的空间，这样不同的子数组就可以有不同个元素了。

int[][] arr = new int[3][];
arr[0] = new int[1];
//创建一个一维数组对象，这个数组对象只有一个int大小
//然后将这个数组的引用赋值给二维数组的子数组的引用变量，
//这个引用变量就是我们下面图解中说的那个专门用来存储子数组的引用的数组的元素，也就是arr[0]
//这个刚创建的数组就是这个二维数组的第一个子数组
arr[1] = new int[2];
//创建一个一维数组对象，这个数组对象只有二个int大小
//然后将这个数组的引用赋值给二维数组的子数组的引用变量arr[1]
//这个刚创建的数组就是这个二维数组的第二个子数组
arr[2] = new int[3];
//创建一个一维数组对象，这个数组对象只有三个int大小
//然后将这个数组的引用赋值给二维数组的子数组的引用变量arr[2]
//这个刚创建的数组就是这个二维数组的第三个子数组

这样最终的二维数组在内存中的存储情况就是：

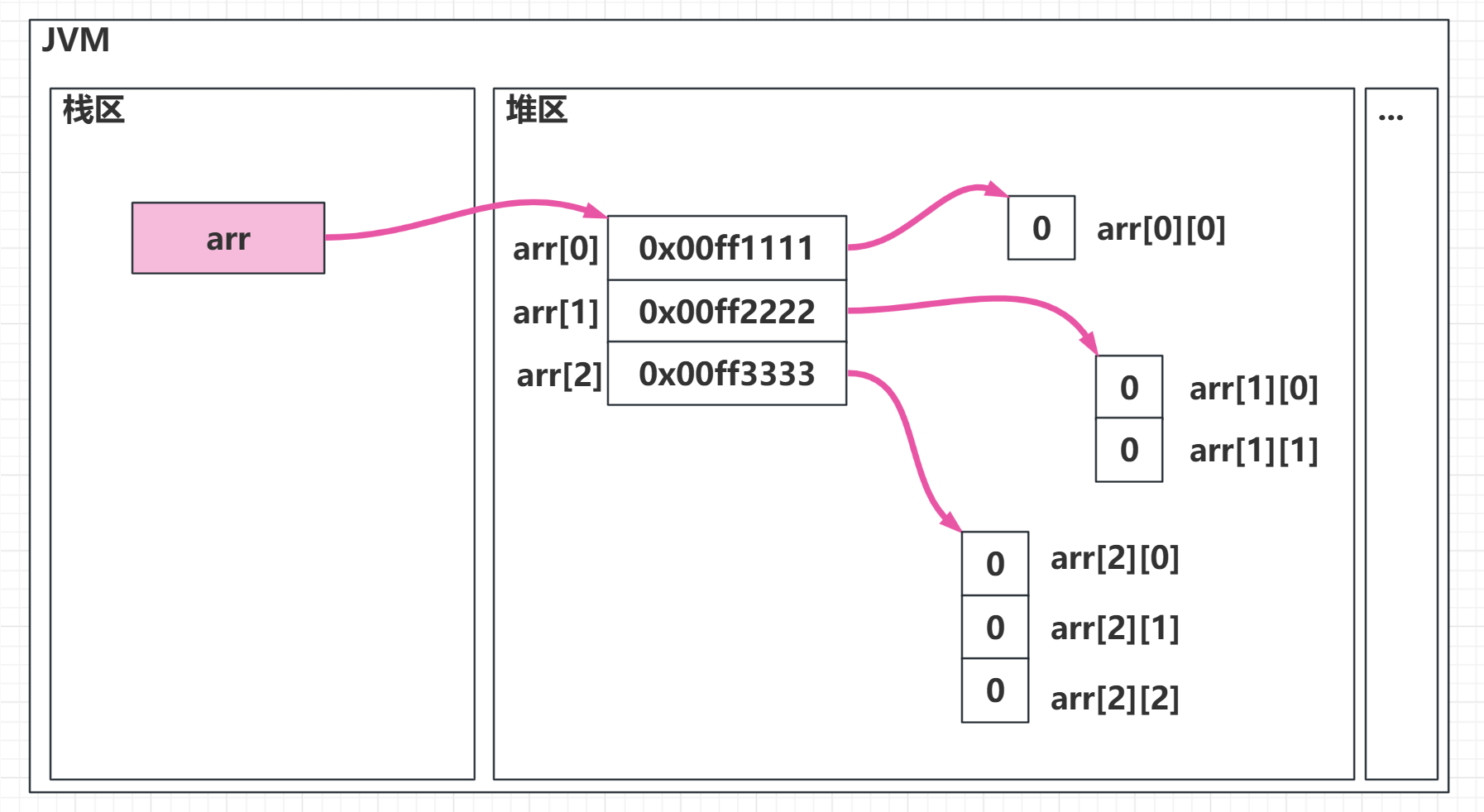
可以发现这里的二维数组的三个子数组的长度是不一样的。

如果我们在声明了二维数组和其行数（或者说其子数组个数）后，没有对其子数组动态分配空间的话，那么对于原来存储子数组的引用的数组存储的元素都应当是 null。

也就是说当我们进行以下语句后：

int[][] arr = new int[3][];

arr 这个二维数组引用变量指向的用来存储其子数组的引用的数组的元素都应当是null，就像下面这样：

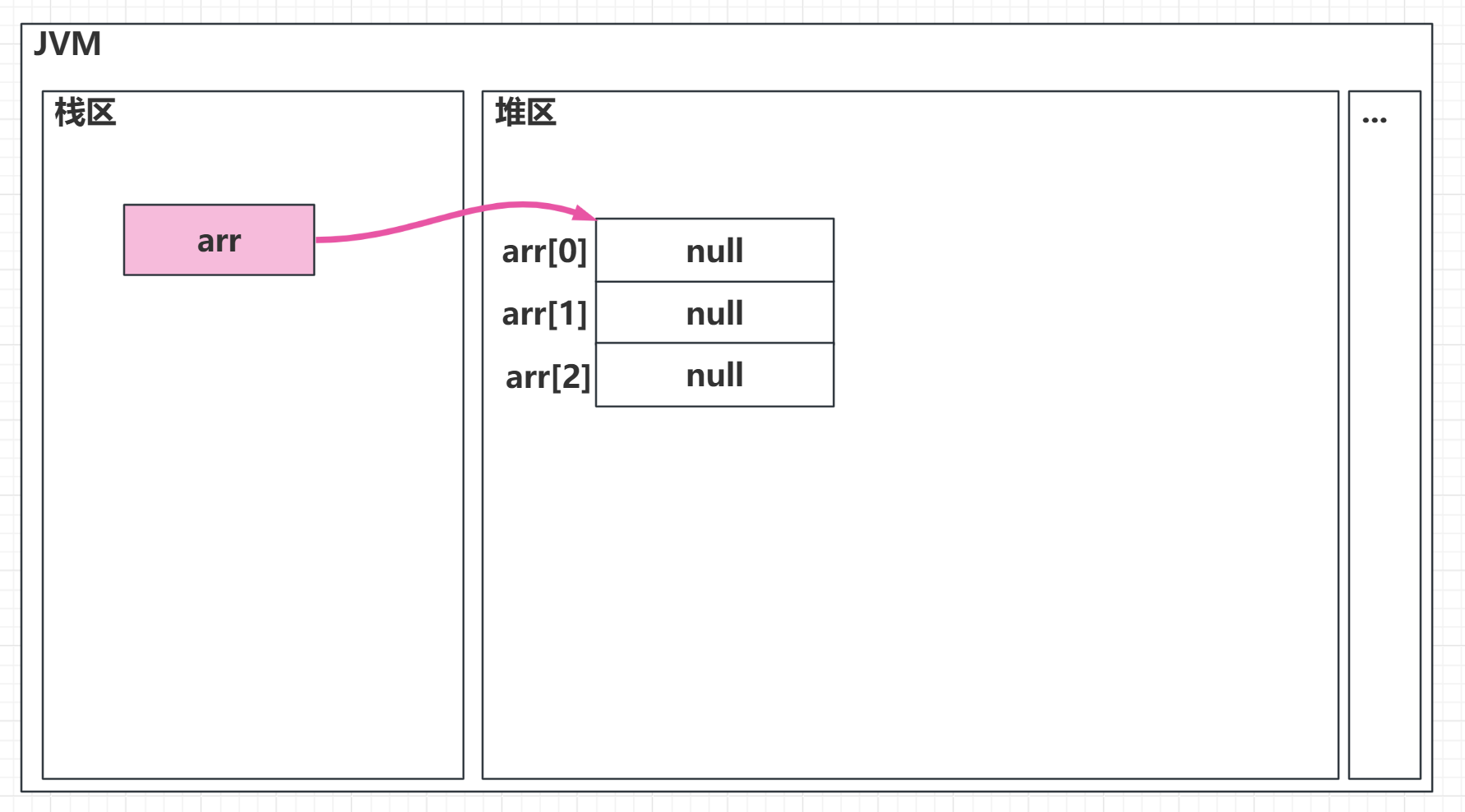
也就是说这时这个二维数组的子数组都还没有被创建。

arr[0] = new int[1];
arr[1] = new int[2];
arr[2] = new int[3];

然后我们依次进行二维数组的每个子数组的创建，然后每个子数组的引用依次存储到图中的这个数组中，然后二维数组引用变量 arr 就与其子数组有了联系。这个二维数组就形成了。

3）列数一样静态创建

与一维数组一致，二维数组也可以使用静态的方式创建：

int[][] arr = {{1, 2, 3}, {2, 3, 4}, {3, 4, 5}};

这里就创建了一个三行三列的二维数组，然后将其元素都赋予特定的值。

4）列数不同静态创建

静态创建也可以使二维数组的每一个子数组的长度不同，只要每个内部的花括号中的元素个数不同就可以了。

int[][] arr = {{1, 2, 3}, {1, 2}, {1}};

这里这样初始化，这个二维数组就有三个子数组，第一个子数组有三个元素，第二个子数组有两个元素，第三个子数组有一个元素，这样也实现了子数组的长度不同，也就是列数不同。

对于静态初始化，如果子数组只有一个元素，花括号也不能省略，因为有了花括号才是一维数组类型，如果没有花括号就是整型了，类型不匹配，就像下面这样是错误的：

int[][] arr = {{1, 2, 3}, {1, 2}, 1};

这里就会报错：

2、二维数组的访问与遍历

1）二维数组的访问

二维数组与一维数组的访问相似，只是多了一个下标，它需要两个下标。

int num = arr[0][0];

这就是访问二维数组 arr 的第一行的第一列的元素，然后赋值给整型变量 num。

2）遍历二维数组的每个元素

对于二维数组 arr，我们使用 .length 获取它的长度，获取的就是它的元素个数，但是对于二维数组，本质就是一维数组的数组，所以这里获取其元素个数就是获取其一维数组的个数，也就是其行数。然后我们使用 arr[i].length 就可以获取每一个二维数组的元素的长度，也就是每一行的元素个数，或者说是列数。

public class Test {
	public static void main(String[] args) {
		int[][] arr = {{1, 2, 3}, {2, 3, 4}, {3, 4, 5}};
		for(int i = 0; i < arr.length; i++) {
			for(int j = 0; j < arr[i].length; j++) {
				System.out.print(arr[i][j] + " ");
			}
			System.out.println("");
		}
	}	
}

运行结果：

二、二维数组细节

1、二维数组的具体存储情况

这里我们使用以下二维数组作为例子来进行讲解：

int[][] arr = new int[2][3];

下面我们进行详细讲解（这里每个元素被默认初始化为 0）：

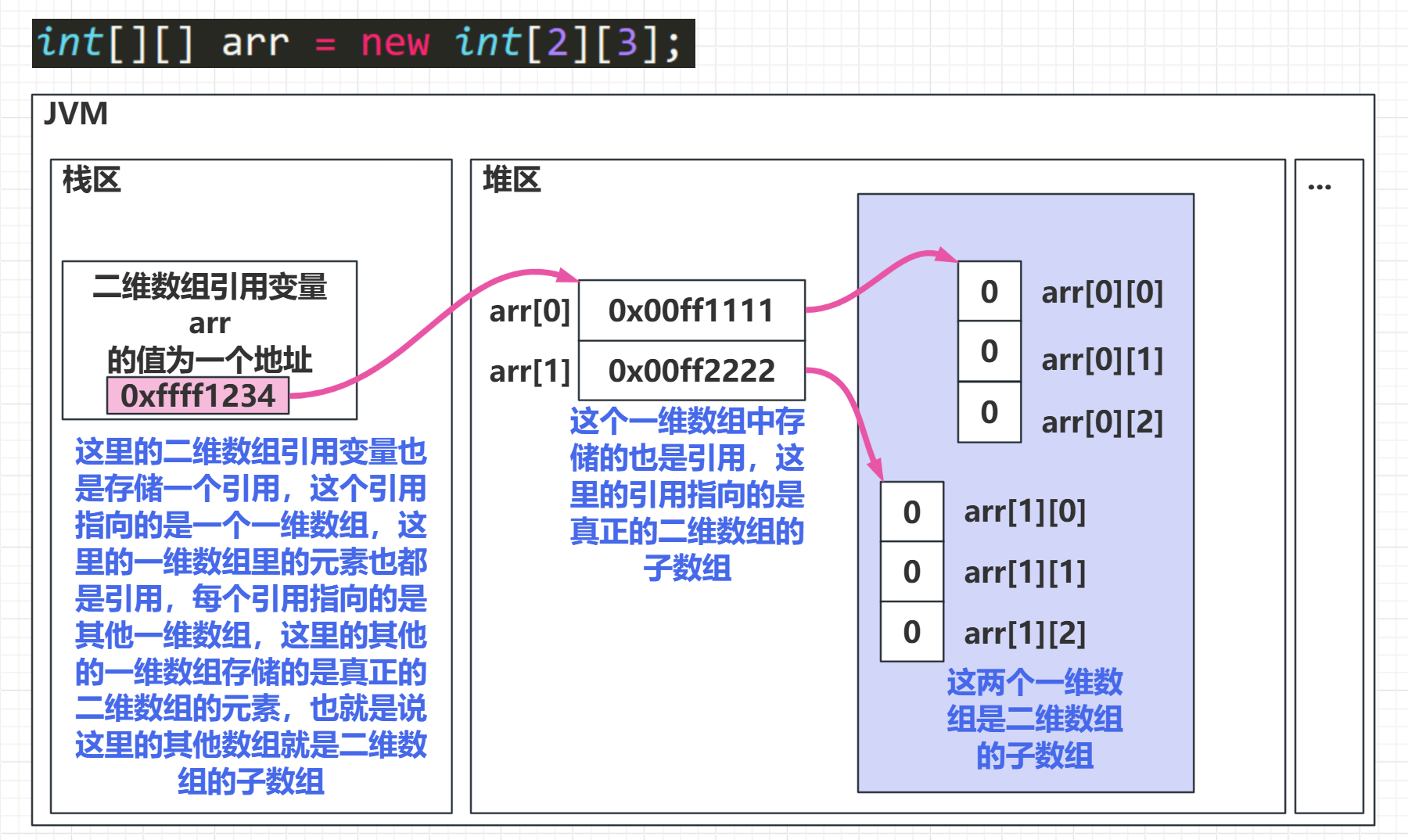
所以对于一个二维数组的创建，不只有二维数组的每个子数组在堆区中存储，还有一个一维数组用来存储每个子数组的引用。

这样做的原因是什么呢，我们下面来解释：

• 支持锯齿状数组（也就是每个子数组的长度可以不同）

众所周知，在 C 语言中，二维数组的每个字数组的长度必须是一致的，而且 C 语言中二维数组的子数组的存储都是连续的。这样才能不需要一个单独的数组来存放子数组的地址就可以访问到所有子数组。

但是，在 Java 中，二维数组的子数组可以是不同的长度，这种设计允许非常灵活的数据结构，而不是强制所有行的长度都相同。而且 Java 的二维数组的子数组在内存上也不一定连续。例如下面这段代码：

int[][] jaggedArray = new int[3][];
jaggedArray[0] = new int[2];
jaggedArray[1] = new int[3];
jaggedArray[2] = new int[1];
{ {0, 0},
  {0, 0, 0},
  {0} }

但是同时也牺牲了内存，因为这样做要多出来一个一维数组用来存储子数组的引用，不然无法访问全部子数组。

• 内存管理与效率

因为二维数组有一个专门存储每一个子数组的引用的数组，所以二维数组的每一行可以单独分配内存，这使得内存管理更加灵活。例如，在需要动态调整某一行的大小时，只需重新分配该行的内存，而不影响整个数组。

这种设计可以利用局部性原理。虽然二维数组的子数组的存储可能在内存中不完全连续，但是访问局部区域的数据可能更高效。因为有一个数组专门存储每一个子数组的引用。

• 提高安全性

Java 提供数组边界检查，防止越界访问。每个子数组作为独立的对象，能更容易地进行边界检查，提高了程序的安全性。

• 简化引用管理

每个数组都是独立的对象，由引用指向，这使得引用计数和垃圾回收更加简单和有效。当一个数组对象不再被引用时，JVM 可以回收其内存。

2、使用代码验证二维数组的存储

我们可以使用代码验证我们上面所提到的二维数组在内存中的存储情况。

public class Test {
	public static void main(String[] args) {
		int[][] arr = new int[2][3];
		System.out.println("二维数组引用变量arr中的引用为：" + arr);
		for(int i = 0; i < arr.length; i++) {
			System.out.println("二维数组用来存储子数组引用的数组的第" + (i + 1) + "个元素arr[" + i + "]为" + arr[i]);
		}
	}	
}

运行结果：

可以发现  arr 这个二维数组引用变量中存储的是用来存储子数组引用的数组的引用。然后就是用来存储子数组引用的数组的每个元素都是一个不同的子数组的引用，同时，我们还发现这两个子数组在内存中的存储明显不连续。

三、二维数组的使用实例与补充

1、遍历一个二维数组求其所有元素之和

public class Test {
	public static void main(String[] args) {
		int[][] arr = {{1, 2, 3}, {1, 2}, {1}};
		int sum = 0;
		for(int i = 0; i < arr.length; i++) {
			for(int j = 0; j < arr[i].length; j++) {
				sum += arr[i][j];
			}
		}
		System.out.println("sum = " + sum);
	}	
}

运行结果：

2、二维数组声明补充

二维数组的声明可以是以下三种方式：

//推荐方式
int[][] arr;
//C语言形式声明
int arr[][];
//
int[] arr[];

第三种声明更能体现二维数组是一维数组的数组。

3、使用二维数组打印杨辉三角

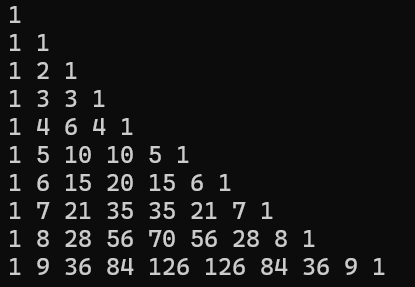
杨辉三角：

第 n 行有 n 项，每一行的第一个和最后一个数字都是 1，其他数字为其上面的两个数字之和。

public class Test {
	public static void main(String[] args) {
		int[][] arr = new int[10][];
		for(int i = 0; i < arr.length; i++) {
			arr[i] = new int[i + 1];
			for(int j = 0; j < arr[i].length; j++) {
				if(j == 0 || j == i) {
					arr[i][j] = 1;
				} else {
					arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
				}
			}
		}
		for(int i = 0; i < arr.length; i++) {
			for(int j = 0; j < arr[i].length; j++) {
				System.out.print(arr[i][j] + " ");
			}
			System.out.println();
		}
	}	
}

运行结果：