目录

一、问题描述

二、解题思路

初始化

遍历边并尝试合并

结果分析

三、代码实现

四、刷题链接

---

一、问题描述

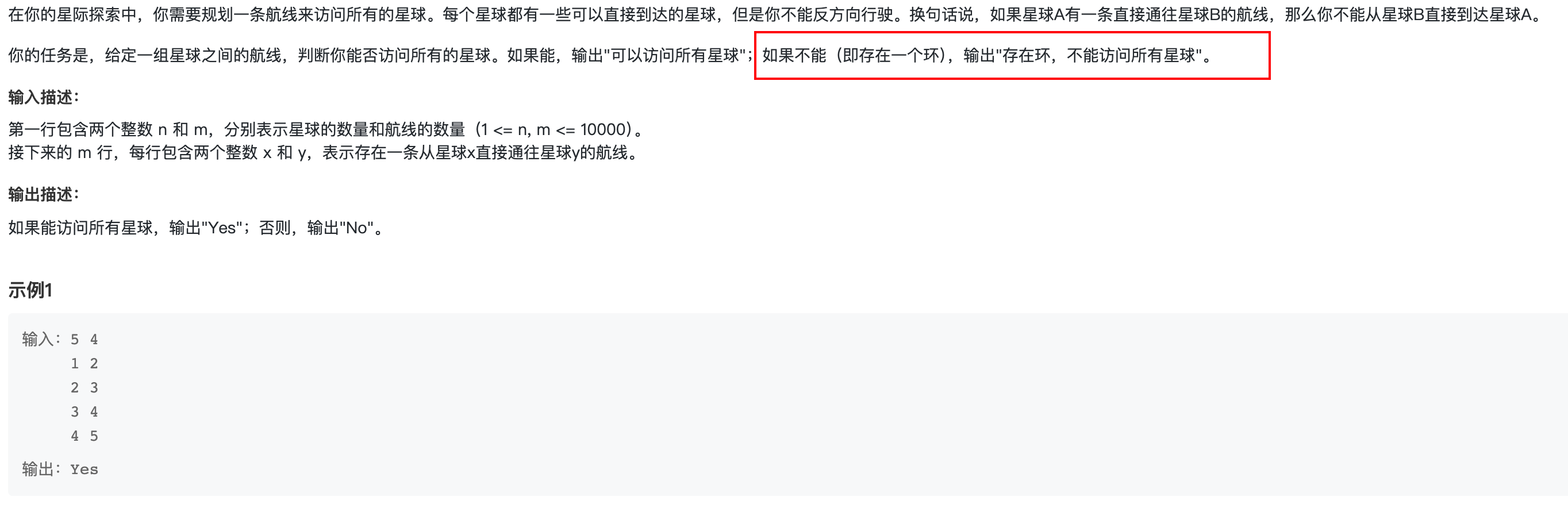
二、解题思路

题目的目的就是检查有向图中是否存在环，这里提供两种判断方式：

1.使用并查集

2.使用拓扑排序

我们在这里先只给出并查集的简单介绍和代码实现

下面是通过Qwen2给出介绍和具体例子：

初始化

每个节点开始时都是单独的集合。我们用列表 parent 来跟踪每个节点的父节点，默认情况下每个节点是其自己的父节点（即 -1 表示没有父节点，表示根节点）。

初始状态如下表所示：

• parent = [A, B, C, D, E] = [-1, -1, -1, -1, -1]

遍历边并尝试合并

1. 第一次遍历：尝试合并节点0（A）和1（B）。由于它们位于不同的集合中，我们可以直接将父节点 parent[B] 设置为 parent[A]。此时，所有从A出发的路径都指向同一个根节点。
2. 第二次遍历：尝试合并节点1（B）和2（C）。同样，我们发现这两个节点位于不同的集合中，因此合并它们。
3. 第三次遍历：尝试合并节点2（C）和3（D），合并后所有从C出发的路径都指向同一个根节点。
4. 第四次遍历：尝试合并节点3（D）和4（E）。这里，我们发现D和E已经位于相同的集合中，因为它们已经被作为B的子集合并过。这意味着边 (D, E) 与之前的路径 (A -> B -> C -> D -> E) 形成了环。

结果分析

由于在尝试合并节点D和E时找到了一个循环（通过A->B->C->D->E），我们可以断定这个有向图中存在环路。因此，我们得出结论：给定的图确实包含至少一个环。

三、代码实现

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    //并查集也可以检验是否有环
    //初始化父结点数组
    static int[] parentArr=new int[10001];
    public static void initParent(int n){//初始化父结点静态数组元素为-1
        for(int i=1;i<=n;i++){
            parentArr[i]=-1;
        }
    }

    public static int find(int x){
        if(parentArr[x]==-1){//当发现是-1时说明到达根节点了
            return x;
        }else{
            int resparent=find(parentArr[x]);
            return resparent;
        }
    }

    public static void union(int x,int y){//合并两个集合
        int xroot=find(x);
        int yroot=find(y);
        if(xroot!=yroot){
            parentArr[yroot]=xroot;
        }
        
    }
    
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int plantnum=in.nextInt();
        int routenum=in.nextInt();
        initParent(plantnum);
        boolean hasLoop=false;
        while (in.hasNextInt()) { //接收星球之间的路线
            int a = in.nextInt();
            int b = in.nextInt();
            if(find(a)!=find(b)){
                union(a,b);
            }else{
                hasLoop=true;
                break;
            }
        }
        if(hasLoop){
            System.out.println("No");
        }else{
            System.out.println("Yes");
        }
    }
    //拓扑排序也可以检验有向无环图是否有环
}

四、刷题链接

星际航线规划_牛客题霸_牛客网