【十大排序算法】归并排序

news2024/11/9 0:54:49

归并排序，如同秋日落叶，分散而细碎，
然而风吹叶动，自然而有序，
彼此相遇，轻轻合拢，
最终成就，秩序之谧。

文章目录

一、归并排序
二、发展历史
三、处理流程
四、算法实现
五、算法特性
六、小结
推荐阅读

一、归并排序

归并排序是一种基于分治思想的排序算法，它将一个待排序的数组分为两个子数组，然后对每个子数组递归地应用归并排序，直到子数组长度为 1。然后，将两个有序的子数组合并成一个有序的数组。这一过程重复进行，直到所有子数组合并成为一个有序的数组。

具体来说，归并排序的步骤如下：

分割： 将待排序数组分为两个子数组，通常是平均分割。
递归排序： 对两个子数组分别递归地应用归并排序，直到子数组长度为 1。
合并： 将两个有序的子数组合并成一个有序的数组。合并过程中，比较两个子数组的第一个元素，将较小（或较大）的元素添加到结果数组中，并将对应子数组的指针向后移动。
重复： 重复以上步骤，直到所有子数组合并成为一个有序的数组。

二、发展历史

归并排序是一种经典的排序算法，其发展历史可以追溯到 $20$ 世纪 $50$ 年代初期。

起源： 归并排序最早由约翰·冯·诺伊曼（John von Neumann）在 $1945$ 年提出，并在他的著作《First Draft of a Report on the EDVAC》中描述了这一算法的基本原理。然而，彼时的计算机硬件水平并不足以支持归并排序的高效实现。
1960 年代： 归并排序在 $1960$ 年代得到了更多的关注和研究。此时，归并排序成为了一种重要的外部排序算法，被应用于磁带排序和数据库系统等领域。在这一时期，归并排序的理论基础逐渐完善，并开始被广泛应用于实际系统中。
1980 年代： 随着计算机硬件的发展和算法研究的深入，归并排序得到了进一步的优化和改进。在 $1980$ 年代，出现了一些新的归并排序的变种和优化算法，例如外部归并排序（External Merge Sort）和自然归并排序（Natural Merge Sort）等。
现代： 在当今计算机科学领域，归并排序仍然是一种非常重要和常用的排序算法。它的理论基础已经得到了深入研究和理解，并且在实际应用中得到了广泛的应用。虽然归并排序的时间复杂度较高，但其稳定性和可预测性使得它在某些场景下具有优势，特别是在外部排序和大规模数据处理等领域。

三、处理流程

场景假设：我们需要将下面的无序序列使用归并排序按从小到大进行排序。
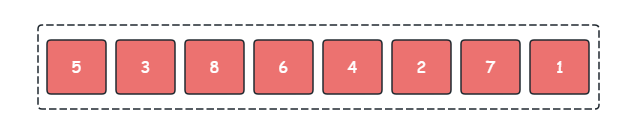
workspace (1).png
归并排序的流程如下：

递归分割序列

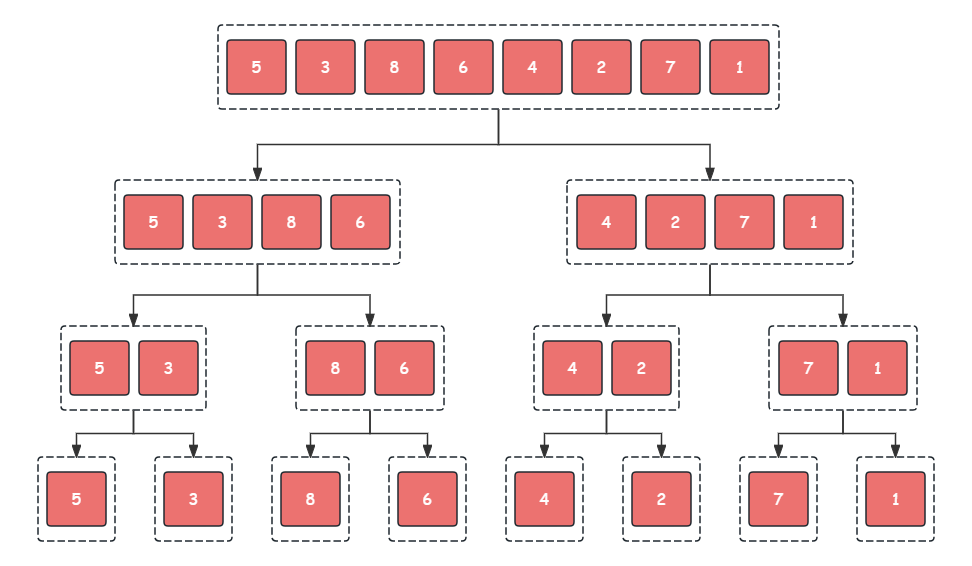
递归合并序列并排序

workspace (2).png

四、算法实现

// 合并两个子数组
void merge(int[] array, int left, int mid, int right) {
    // 计算左右子数组的长度
    int leftLength = mid - left + 1;
    int rightLength = right - mid;

    // 创建临时数组存储左右子数组
    int[] leftArray = new int[leftLength];
    int[] rightArray = new int[rightLength];

    // 将数据拷贝到临时数组
    System.arraycopy(array, left, leftArray, 0, leftLength);
    System.arraycopy(array, mid + 1, rightArray, 0, rightLength);

    int i = 0, j = 0;
    int k = left;
    // 合并两个子数组
    while (i < leftLength && j < rightLength) {
        if (leftArray[i] <= rightArray[j]) {
            array[k++] = leftArray[i++];
        } else {
            array[k++] = rightArray[j++];
        }
    }

    // 处理剩余元素
    while (i < leftLength) {
        array[k++] = leftArray[i++];
    }

    while (j < rightLength) {
        array[k++] = rightArray[j++];
    }
}

// 递归地进行归并排序
void mergeSort(int[] array, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        // 递归地对左右子数组进行归并排序
        mergeSort(array, left, mid);
        mergeSort(array, mid + 1, right);
        // 合并左右子数组
        merge(array, left, mid, right);
    }
}

public static void main(String args[]) {
    int[] array = {12, 11, 13, 5, 6, 7};
    System.out.println("原始数组：");
    for (int num : array) {
        System.out.print(num + " ");
    }
    System.out.println();

    // 调用归并排序算法
    mergeSort(array, 0, array.length - 1);

    System.out.println("\n排序后的数组：");
    for (int num : array) {
        System.out.print(num + " ");
    }
}

算法时间复杂度分析：

情况	时间复杂度	计算公式	公式解释
最好情况	$O (n l o g n)$	$2T(\frac{n}{2}) + n$	归并排序在所有情况下都会将数组分成两半，然后递归地对它们进行排序，最后再将它们合并。这个过程的时间复杂度始终为 $O (n l o g n)$ 。其中， $n$ 是数组的长度， $l o g n$ 是因为每次都将数组分成两半。
平均情况	$O (n l o g n)$	$2T(\frac{n}{2}) + n$	同上
最坏情况	$O (n l o g n)$	$2T(\frac{n}{2}) + n$	同上