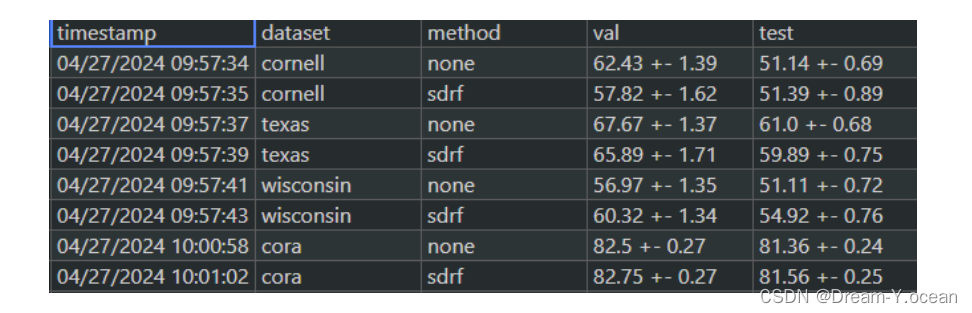
题目


思路来源
quality代码
题解
对n个泳姿点(ai,bi)建凸包,实际上是一个上凸壳,
对于询问(ci,di)来说,抽象画一下这个图,箭头方向表示询问向量
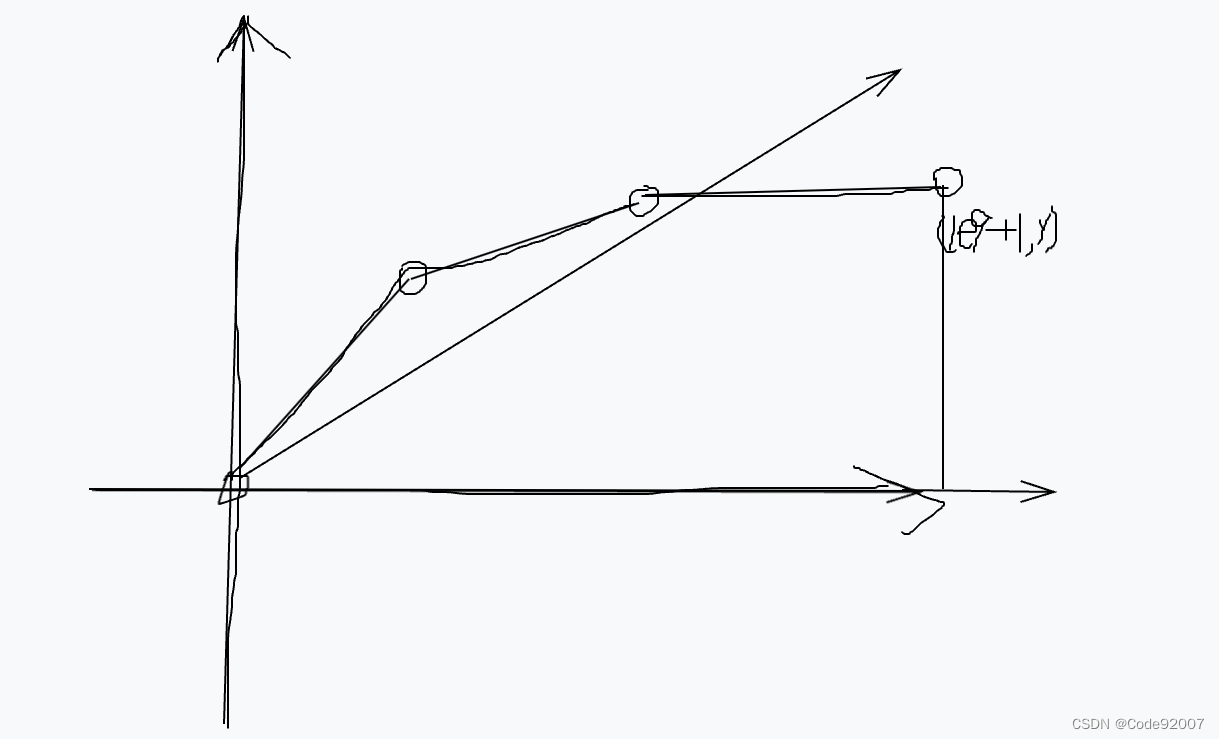
按x轴排增序,并且使得后面的y不小于前面的y,因为总可以多耗费体力达到相同的米数
新增一个点(0,0),新增一个点(1e9+1,y),其纵坐标与最后一个点纵坐标相同
对于询问的向量,求它与上凸壳的交点,显然用这个方向的向量是最优的
1. 如果询问的向量在上凸壳第一个点逆时针方向,无解
2. 如果与上凸壳有交点,
显然这个封闭图形内的点都是可以用各种泳姿1s凑出来的,那么交点方向最优,
只需看(ci,di)中的di,是交点处的纵坐标的几倍即可,答案即为这个倍数
3. 如果向量与竖直的这条边有交点,那么最后相当于多耗费体力的情况下1s也可以跑这么多米
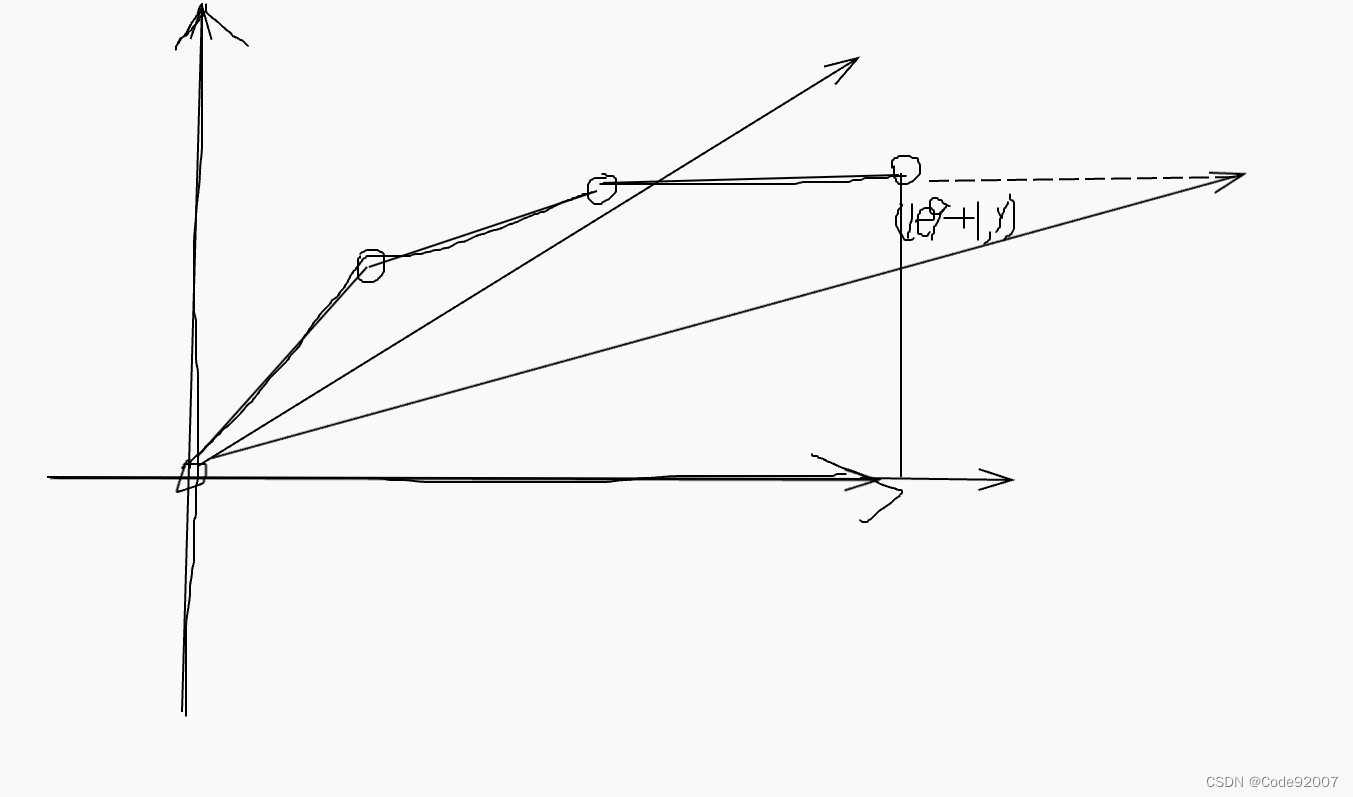
那么,两条直线还是有交点的,只是向量与水平直线的交点,
实际用的仍然是交点这个向量,只是实际的含义是y相同的情况下多耗费了体力
然后qls的二分写的就很妙,统一了这三种情况,以及交点恰好是凸包的一个点的情况
我写的就很不优雅,需要讨论三种情况,判断l=0,l=n-1
代码1(qls)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
typedef long double db;
struct Point
{
ll x,y;
int id;
Point() {}
Point(ll _x,ll _y):x(_x),y(_y) {}
Point operator - (const Point& t)const
{
return Point(x-t.x,y-t.y);
}
ll operator * (const Point& t)const
{
return x*t.y-y*t.x;
}
};
vector<Point> Graham(vector<Point> p)
{
p.insert(p.begin(),Point(0,0));
sort(p.begin(),p.end(),[](const Point& lhs,const Point& rhs)
{
return lhs.x==rhs.x ? lhs.y<rhs.y : lhs.x<rhs.x;
});
for(size_t i=1; i<p.size(); i++)
p[i].y=max(p[i].y,p[i-1].y);
p.emplace_back(1000000001,p.back().y);
vector<Point> res;
for(auto& t : p)
{
while(res.size()>1 && (t-res.back())*(t-res[res.size()-2])<=0)res.pop_back();
res.push_back(t);
}
res.erase(res.begin());
return res;
}
int main()
{
int n;
scanf("%d",&n);
vector<Point> p(n);
for(int i=0; i<n; i++)
scanf("%lld%lld",&p[i].x,&p[i].y);
p=Graham(p);
n=p.size();
int q;
scanf("%d",&q);
while(q--)
{
Point que;
scanf("%lld%lld",&que.x,&que.y);
if(que*p[0]<0)
{
printf("-1\n");
continue;
}
int l=0,r=n-2;//l<=r+1
while(l<r)//>0 =0 <0 或>0 <0渐变
{
int m=(l+r+1)/2;
if(que*p[m]>0)l=m;
else r=m-1;
}
db k1=1.0L*(p[l+1].y-p[l].y)/(p[l+1].x-p[l].x);
db b1=p[l].y-k1*p[l].x;
db k2=1.0L*que.y/que.x;
db x=b1/(k2-k1),y=k2*x;
printf("%.18Lf\n",que.y/y);
}
return 0;
}
代码2(我的二分)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
typedef long double db;
struct Point
{
ll x,y;
int id;
Point() {}
Point(ll _x,ll _y):x(_x),y(_y) {}
Point operator - (const Point& t)const
{
return Point(x-t.x,y-t.y);
}
ll operator * (const Point& t)const
{
return x*t.y-y*t.x;
}
};
vector<Point> Graham(vector<Point> p)
{
p.insert(p.begin(),Point(0,0));
sort(p.begin(),p.end(),[](const Point& lhs,const Point& rhs)
{
return lhs.x==rhs.x ? lhs.y<rhs.y : lhs.x<rhs.x;
});
for(size_t i=1; i<p.size(); i++)
p[i].y=max(p[i].y,p[i-1].y);
p.emplace_back(1000000001,p.back().y);
vector<Point> res;
for(auto& t : p)
{
while(res.size()>1 && (t-res.back())*(t-res[res.size()-2])<=0)res.pop_back();
res.push_back(t);
}
res.erase(res.begin());
return res;
}
int main()
{
int n;
scanf("%d",&n);
vector<Point> p(n);
for(int i=0; i<n; i++)
scanf("%lld%lld",&p[i].x,&p[i].y);
p=Graham(p);
n=p.size();
int q;
scanf("%d",&q);
while(q--)
{
Point que;
scanf("%lld%lld",&que.x,&que.y);
if(que*p[0]<0)
{
printf("-1\n");
continue;
}
int l=0,r=n-1;
while(l<=r){
int m=(l+r)/2;
if(que*p[m]>0)l=m+1;
else r=m-1;
}
l--;
if(l<0)l=0;
if(l==n-1)l--;
//if(l==n-1)l--;
db k1=1.0L*(p[l+1].y-p[l].y)/(p[l+1].x-p[l].x);
//k1=0 b1=5 k2=8/6 x=5/(8/6)=30/8 y=30/6=5
db b1=p[l].y-k1*p[l].x;
db k2=1.0L*que.y/que.x;
db x=b1/(k2-k1),y=k2*x;
printf("%.18Lf\n",que.y/y);
}
return 0;
}