红黑树的介绍与实现

news2024/12/23 7:31:02

前言

前面我们介绍了AVL树，AVL树是一棵非常自律的树，有着严格的高度可控制！但是正它的自律给他带来了另一个问题，即虽然他的查找效率很高，但是插入和删除由于旋转而导致效率没有那么高。我们上一期的结尾说过经常修改的话就不太适合AVL树了，而红黑树更加适合！OK，本期就来介绍一下赫赫有名的红黑树！

本期内容介绍

什么是红黑树

红黑树的实现

红黑树的效率分析以及应用

什么是红黑树？

红黑树是1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的 " 红黑树 "。

红黑树是一种二叉搜索树，但在每个结点上增加了一个存储位表示结点的颜色，可以是红色或是黑色；通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径比其他的路径长出两倍，因而是接近平衡的！

OK，这就是一棵红黑树：

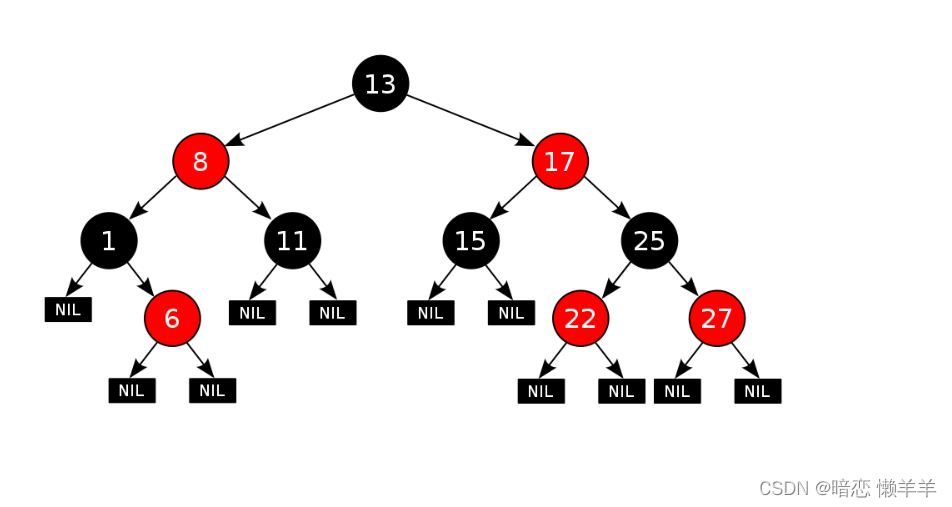
最长节点的路径就是一黑一红的交替，最短的就是两黑：

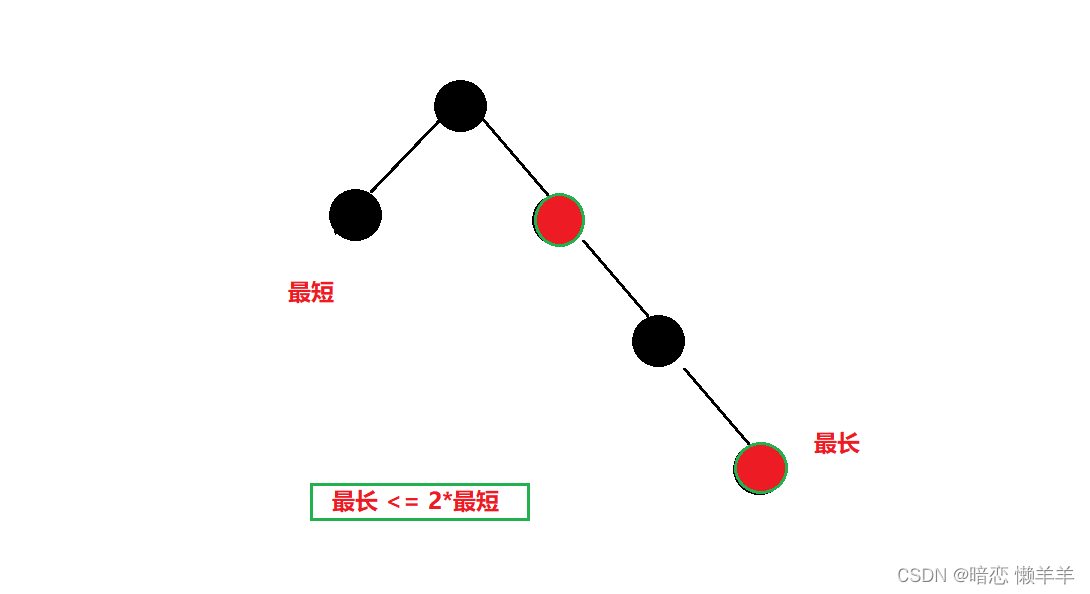
红黑树的性质

1、每个结点要么是红色，要么是黑色

2、根节点是黑色

3、如果一个结点是红色，则它的两个孩子结点是黑色

4、对于任意一个节点，从该结点到其所有的后代叶子结点的简单路径上，均包含相同的黑色结点

5、每个叶子结点就是黑色的（此处的叶子结点指的是空节点）

上面的这5条性质就是限制红黑树平衡的规则！其中4最重要的下来是3，基本所有的操作都是围着4进行的！！！

红黑树的实现

OK，上面介绍了红黑树是一种二叉搜索树，只不过是在每个结点添加了一个存储颜色的颜色位，所以它的大框架还是和搜索树一样的，所以我们就先搭一个框架出来！

enum Col//颜色
{
	RED,
	BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;//左孩子
	RBTreeNode<K, V>* _right;//右孩子
	RBTreeNode<K, V>* _parent;//父结点
	pair<K, V> _kv;//数据域
	Col _col;//颜色

	RBTreeNode(const pair<K,V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_col(RED)//新插入的节点默认是红色
	{}
};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	RBTree()
		:_root(nullptr)
		,_size(0)
	{}

private:
	Node* _root;//根节点
	size_t _size;//节点的数量
};

思考：新插入的节点应该是红色还是黑色？为什么？

新插入的节点一定是红色！

因为新插入的节点是红色可能违反性质3，但一定不违反性质4！

如果新插入的是黑色，一定违反性质4，也就是在部分子路径上增加了黑色节点。所以插入的新节点一定是红色，即使红色违反了性质3也是比较好控制的！

OK，这里依旧是采用的三叉链，原因是方便找父亲：

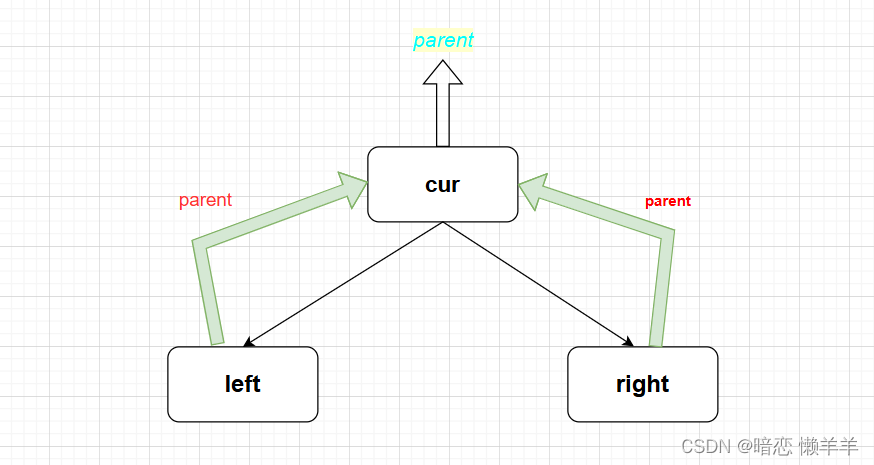
红黑树的插入

上面介绍了，红黑树的本质是一种二叉搜索树，所以先不管它的颜色和高度如何调节，先把搜索树的那一套给整出来：

bool Insert(const pair<K, V>& kv)
{
	Node* cur = _root;//当前节点
	Node* parent = nullptr;//插入位置的父亲

	//第一次插入
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_root->_col = BLACK;//根节点是黑色
		return true;
	}

	//寻找插入的位置
	while (cur)
	{
		if (cur->_kv.first < kv.first)//插入节点的key比当前节点的key大
		{
			parent = cur;
			cur = cur->_right;//去右边找
		}
		else if(cur->_kv.first > kv.first)//插入节点的key比当前节点的key小
		{
			parent = cur;
			cur = cur->_left;//去左边找
		}
		else
		{
			return false;//插入的节点存在
		}
	}

	//找到插入位置
	cur = new Node(kv);
	//链接
	if (parent->_kv.first > cur->_kv.first)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}
	cur->_parent = parent;

	//颜色和高度调整
	//....

	return true;
}

OK，还是先来验证一下当前的逻辑对不对，所以走个中序看看是不是有序即可：由于中序要根节点，而类外面是无法访问的，所以我们还是和以前一样搞成子函数或提供get和set方法；这里就搞成子函数了：

中序遍历

void _InOrder(Node* root)
{
	if (root == nullptr)
		return;
		
	_InOrder(root->_left);
	cout << root->_kv.first << ":" << root->_kv.second << endl;
	_InOrder(root->_right);
}

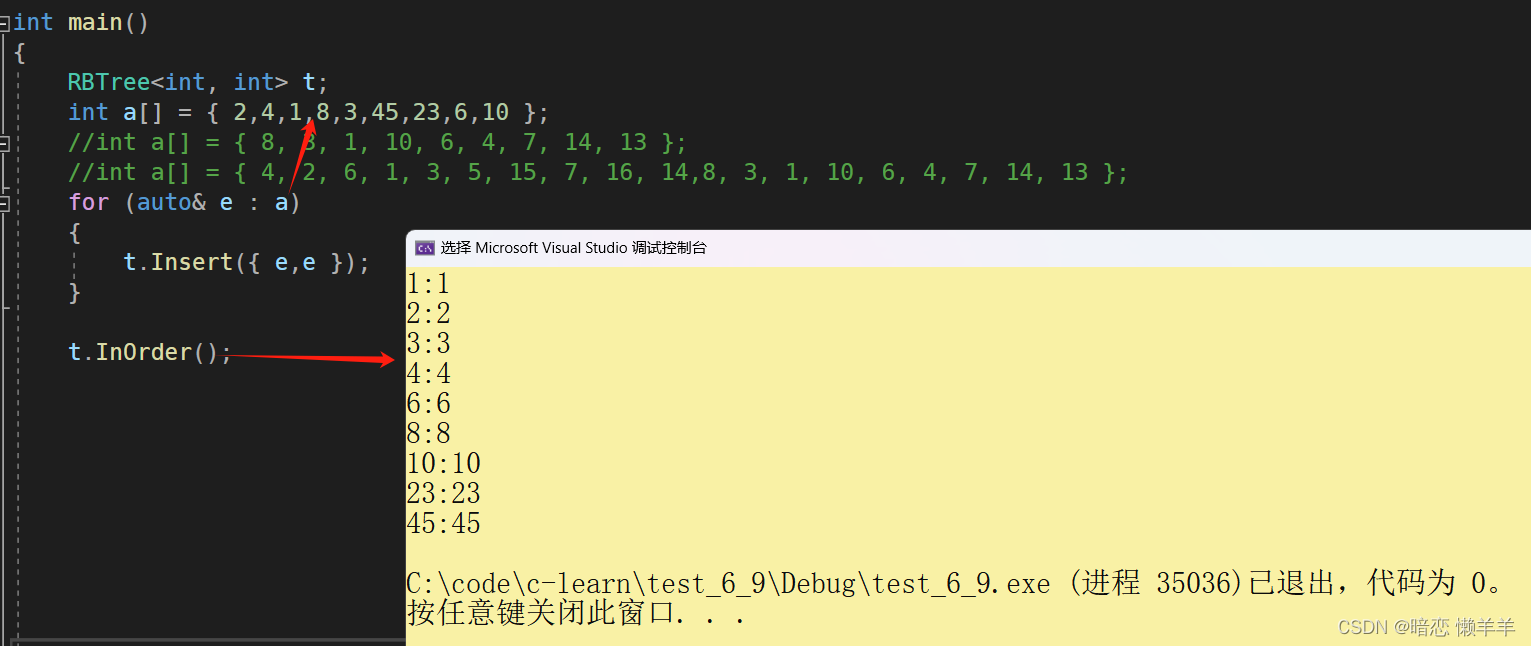
OK，没问题，下面我们就来讨论一下红黑树的维持平衡的方式:变色和旋转！

红黑树的变色和旋转

由于新插入的节点一定是红色的，此时分为两种情况，1、父亲为黑  2、父亲为红

如果父亲为黑，不违反任何性质，插入结束；

如果父亲为红，看看叔叔，此时叔叔有三类情况：1、叔叔存在且为红  2、叔叔不存在  3、叔叔存在为黑

如果，叔叔存在且为红：变色（将父亲和叔叔变黑色，将爷爷变红色），继续更新

如果，叔叔不存在或存在且为黑，旋转 + 变色（如果孩子是父亲的左/右，先对孩子父亲进行左/右旋，在对爷爷进行左/右）

OK，这里看着可能会有些迷，看看下面的导图会很清楚：

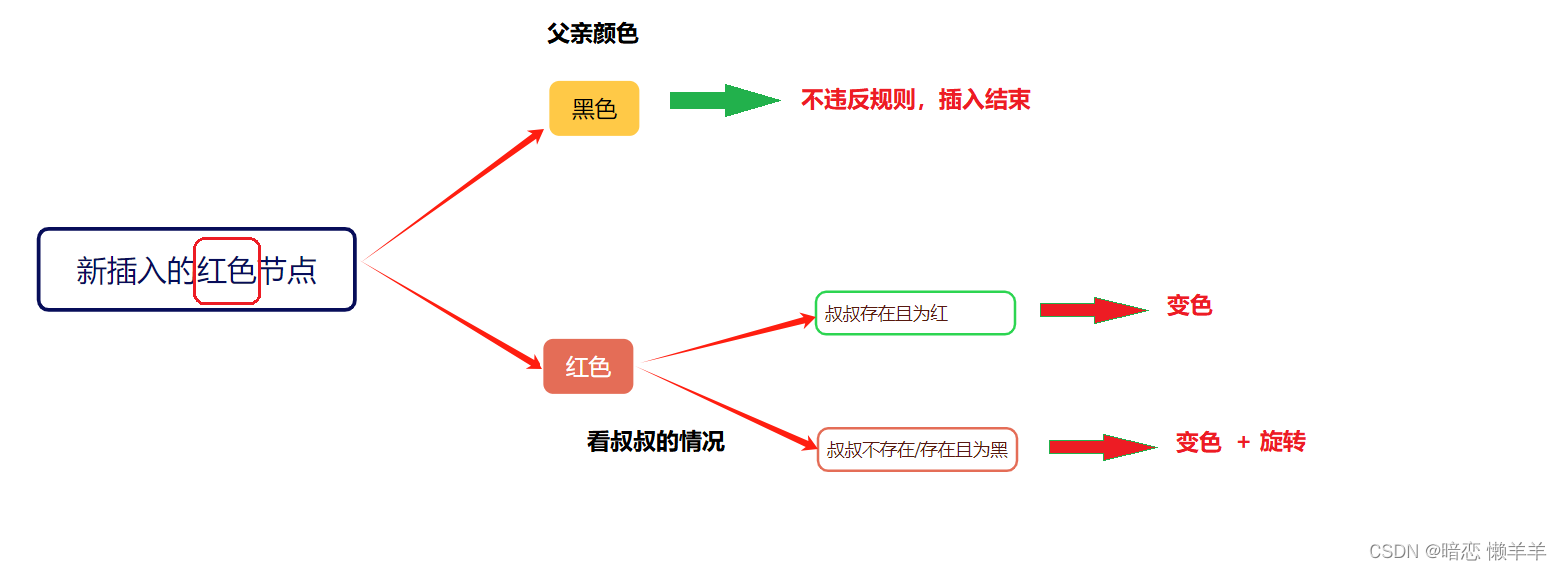
OK，理解了上述的表达，下面我来画图解释一下：

parent是黑色插入结束

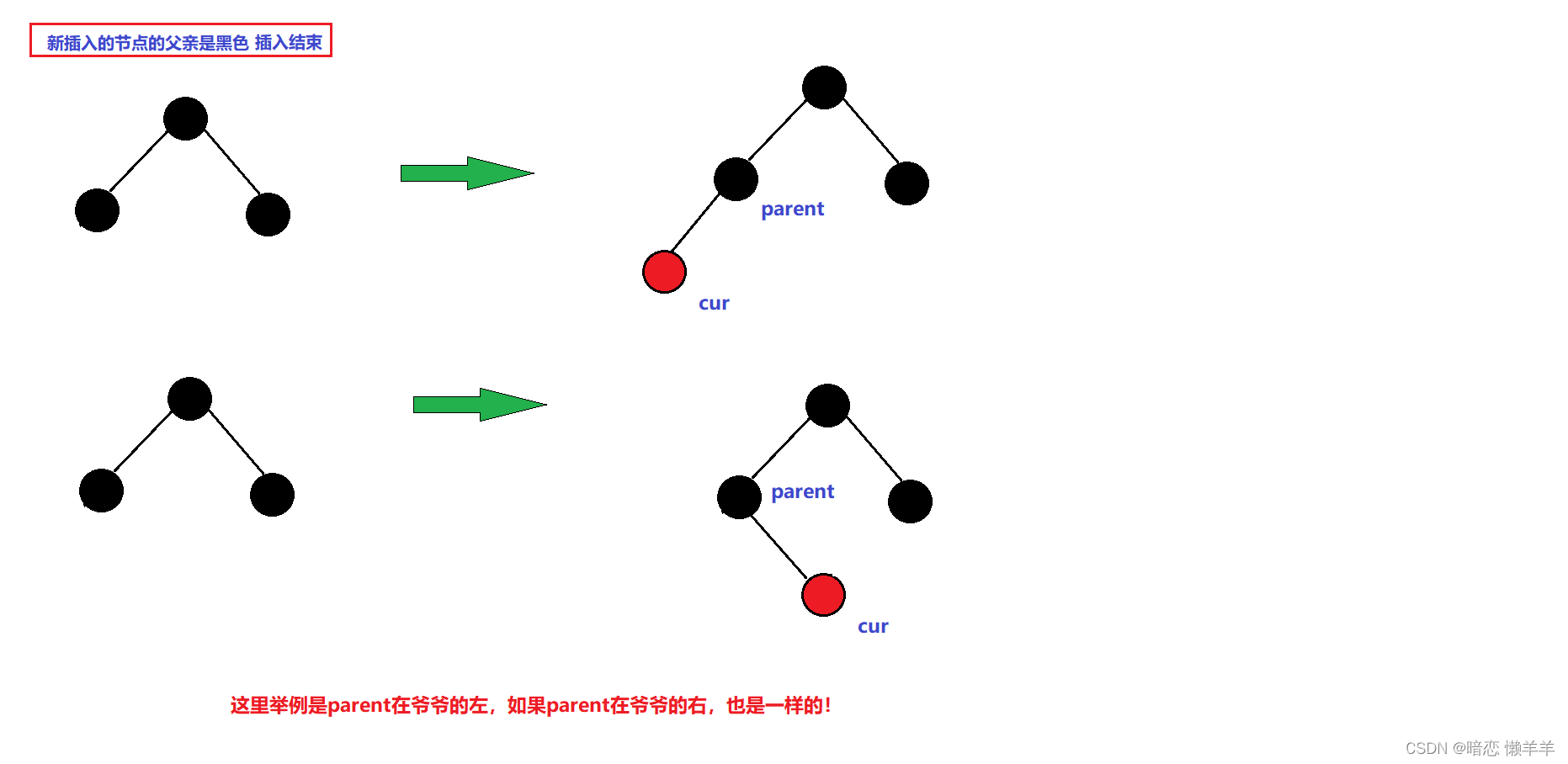
parent为红，叔叔存在且为红（变色）

父亲和叔叔变黑，爷爷变红，继续向上更新

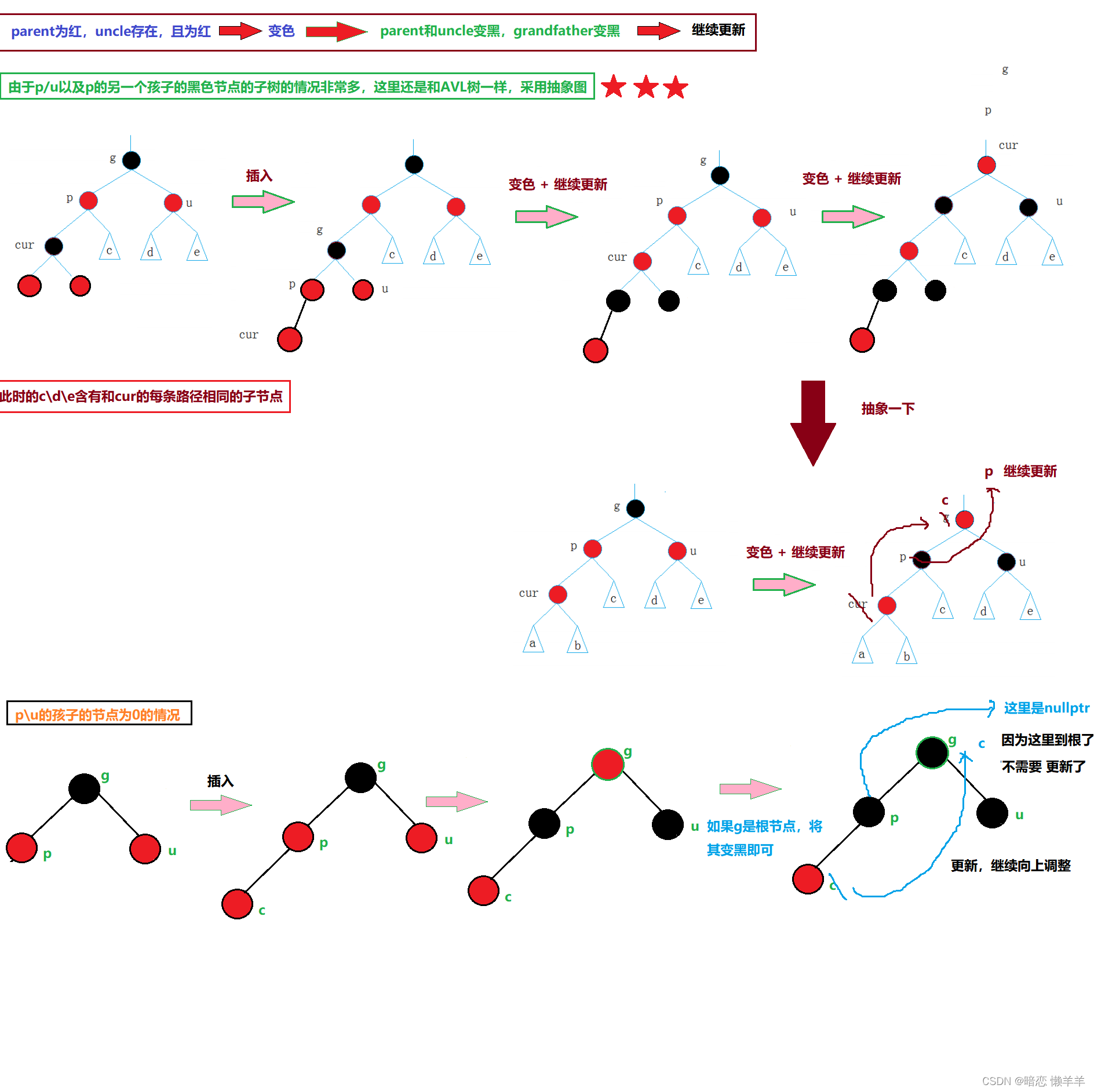
这里只画了parent在爷爷的左边的情况，如果parent在爷爷的右边和这个是一样的！

parent为红，叔叔不存在会存在为黑（变色 + 旋转）

如果parent在爷爷的左，且cur在父亲的左，对爷爷进行右单旋；

如果parent在爷爷的左，且cur在父亲的右，先对parent左单旋，在对爷爷进行右单旋；

如果parent在爷爷的右，且cur在父亲的右，对爷爷进行左单旋；

如果parent在爷爷的右，且cur在父亲的左，先对parent右单旋，在对爷爷进行左单旋；

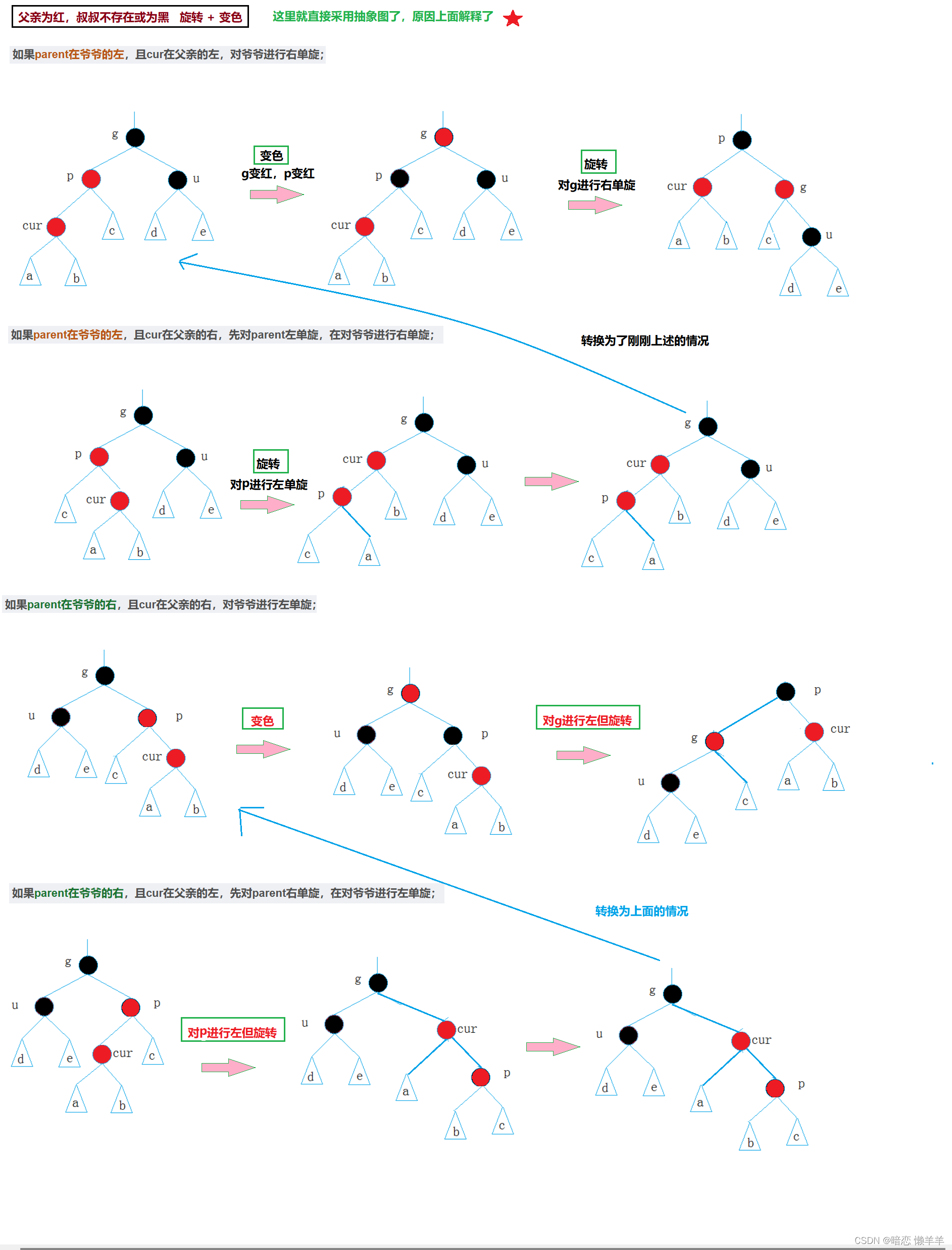
OK，废话不多说直接上代码：

bool Insert(const pair<K, V>& kv)
{
	Node* cur = _root;//当前节点
	Node* parent = nullptr;//插入位置的父亲

	//第一次插入
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_size++;//插入成功节点数+1
		_root->_col = BLACK;//根节点是黑色
		return true;
	}

	//寻找插入的位置
	while (cur)
	{
		if (cur->_kv.first < kv.first)//插入节点的key比当前节点的key大
		{
			parent = cur;
			cur = cur->_right;//去右边找
		}
		else if(cur->_kv.first > kv.first)//插入节点的key比当前节点的key小
		{
			parent = cur;
			cur = cur->_left;//去左边找
		}
		else
		{
			return false;//插入的节点存在
		}
	}

	//找到插入位置
	cur = new Node(kv);
	//链接
	if (parent->_kv.first > cur->_kv.first)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}
	cur->_parent = parent;

	//颜色和高度调整
	while (parent && parent->_col == RED)
	{
		Node* grandfather = parent->_parent;
		if (parent == grandfather->_left)//父亲在爷爷的左
		{
			Node* uncle = grandfather->_right;//叔叔就是父亲的右
			//父亲存在且为红 -> 变色
			if (uncle && uncle->_col == RED)
			{
				grandfather->_col = RED;
				parent->_col = uncle->_col = BLACK;
				//继续向上调整
				cur = grandfather;
				parent = cur->_parent;
			}
			else//叔叔不存在或存在但为黑 -> 变色 + 旋转
			{
				if (cur == parent->_left)//cur在父亲的左
				{
					//		   g
					//	   p		u
					// c
					RotateR(grandfather);//旋转
					parent->_col = BLACK;//变色
					grandfather->_col = RED;
				}
				else//cur在父亲的右
				{
					//		  g
					//	  p		  u
					//        c
					RotateL(parent);//旋转
					RotateR(grandfather);
					cur->_col = BLACK;//变色
					grandfather->_col = RED;
				}

				break;//旋转后不需要再向上更新了
			}
		}
		else//parent在爷爷的右
		{
			Node* uncle = grandfather->_left;//叔叔在父亲的左
			//叔叔存在且为红 -> 变色
			if (uncle && uncle->_col == RED)
			{
				grandfather->_col = RED;
				parent->_col = uncle->_col = BLACK;
				//继续向上调整
				cur = grandfather;
				parent = cur->_parent;
			}
			else//叔叔不存在或存在但为黑 -> 变色 + 旋转
			{
				if (cur == parent->_left)//cur在父亲的左 
				{
					//		  g
					//	  u		   p
					//        c
					RotateR(parent);//旋转
					RotateL(grandfather);
					cur->_col = BLACK;//变色
					grandfather->_col = RED;
				}
				else
				{
					//		  g
					//	  u		   p
					//                 c
					RotateL(grandfather);//旋转
					parent->_col = BLACK;//变色
					grandfather->_col = RED;
				}

				break;//旋转后不需要再向上更新了
			}
		}
	}

	_root->_col = BLACK;//保证根节点永远是黑色
	_size++;//插入成功节点数+1

	return true;
}

旋转

红黑树的旋转没有，AVL的复杂，只有左右单旋且没有平衡因子！整体的逻辑和AVL一样的，这里不在详细介绍了！

void RotateR(Node* parent)
{
	Node* subL = parent->_left;//父亲的左
	Node* subLR = subL->_right;//左子树的右
	Node* ppNode = parent->_parent;//parent的父节点,方便旋转后的链接

	parent->_left = subLR;//将左子树的右给父亲的做
	if (subLR)
		subLR->_parent = parent;

	subL->_right = parent;//parent做左子树的右
	parent->_parent = subL;

	if (parent == _root)//parent是根
	{
		_root = subL;//此时的新根就是subL
		ppNode = nullptr;
	}
	else//parent不是根
	{
		//将新的根连接到ppNode
		if (ppNode->_left == parent)
		{
			ppNode->_left = subL;
		}
		else
		{
			ppNode->_right = subL;
		}
		subL->_parent = ppNode;
	}
}

void RotateL(Node* parent)
{
	Node* subR = parent->_right;//父亲的右
	Node* subRL = subR->_left;//右子树的左
	Node* ppNode = parent->_parent;//parent的父节点,方便旋转后的链接

	parent->_right = subRL;//将右子树的左连接到parent的右
	if (subRL)
		subRL->_parent = parent;

	subR->_left = parent;//parent连接到subR的左
	parent->_parent = subR;

	if (parent == _root)//parent是根
	{
		_root = subR;//此时的新根就是subR
		ppNode = nullptr;
	}
	else//parent不是根
	{
		//将新的根连接到ppNode
		if (ppNode->_left == parent)
		{
			ppNode->_left = subR;
		}
		else
		{
			ppNode->_right = subR;
		}
		subR->_parent = ppNode;
	}
}

OK，我们验证一下，判断一下是否是平衡的：

是否平衡

先获取任意一条路径的黑色节点，然后通过dfs进行检查每个结点是不是符合红黑树的规则！

如果出现连续的红色节点，不符合！判断方式：当出现红色节点时，检查其父节点是否是红色的，如果是则不符合！

如走到空了，检查该条路径的黑色节点和一开始求出的是否一致，不一致则不符合！

当前节点符合，去检查其左右！

bool IsBalance()
{
	if (_root && _root->_col == RED)
	{
		return false;//根为红，一定不是红黑树
	}

	int black = 0;//获取任意一条路径的黑色节点（这里是最左路）
	Node* cur = _root;
	while (cur)
	{
		if (cur->_col == BLACK)
		{
			black++;
		}

		cur = cur->_left;
	}

	return Check(_root, black, 0);
}
bool Check(Node* root, const int black, int num)
{
	if (root == nullptr)
	{
		//当走到叶子节点的时候和其他路径的黑色节点的个数不一样
		if (black != num)
		{
			return false;
		}

		return true;
	}

	//存在连续的红色节点
	if (root->_col == RED && root->_parent && root->_parent->_col == RED)
	{
		cout << root->_kv.first << " ：存在连续的红色节点" << endl;
		return false;
	}

	//遇到黑色节点++
	if (root->_col == BLACK)
	{
		num++;
	}

	//当前节点符合红黑树，它的左右子树也要都符合
	return Check(root->_left, black, num) && Check(root->_right, black, num);
}

OK，验证一下：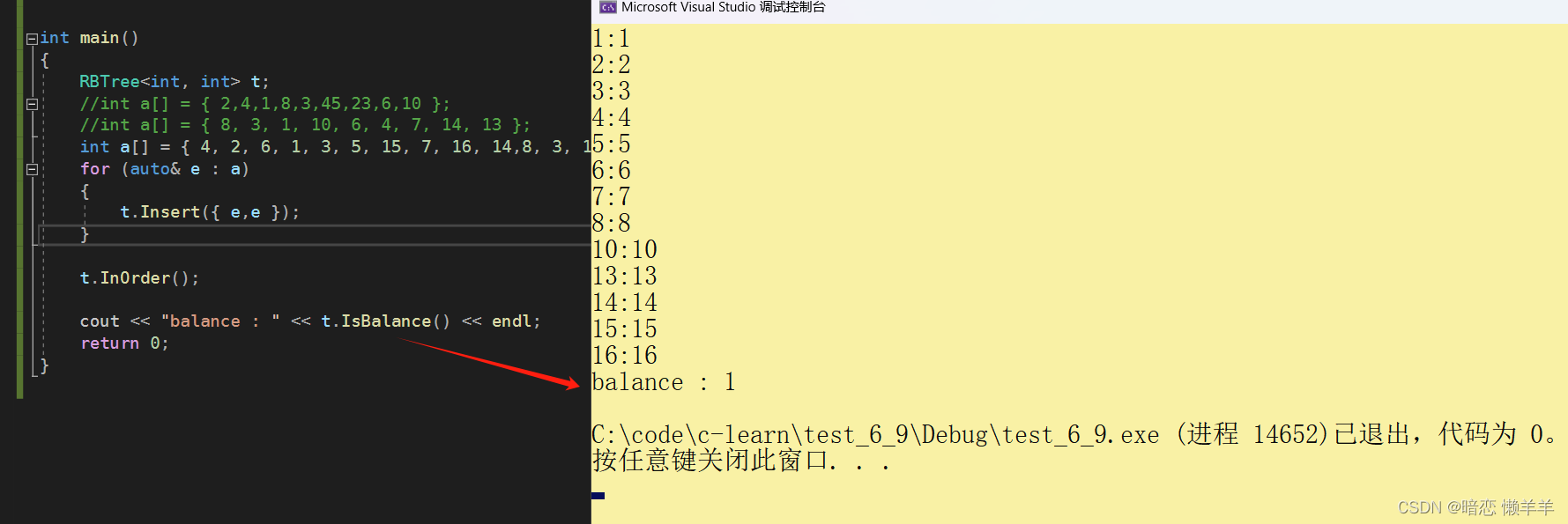

OK，么有问题！下面把其他的接口补一下！

Size

由于我们提前记录了_size所以直接返回成员_size即可！

size_t Size()
{
	return _size;
}

Find

和以前的搜索树一样，大了去右边找，小了去左边找！

Node* Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_kv.first < key)//插入节点的key比当前节点的key大
		{
			cur = cur->_right;//去右边找
		}
		else if (cur->_kv.first > key)//插入节点的key比当前节点的key小
		{
			cur = cur->_left;//去左边找
		}
		else
		{
			return cur;//找到了
		}
	}

	return nullptr;//没找到
}

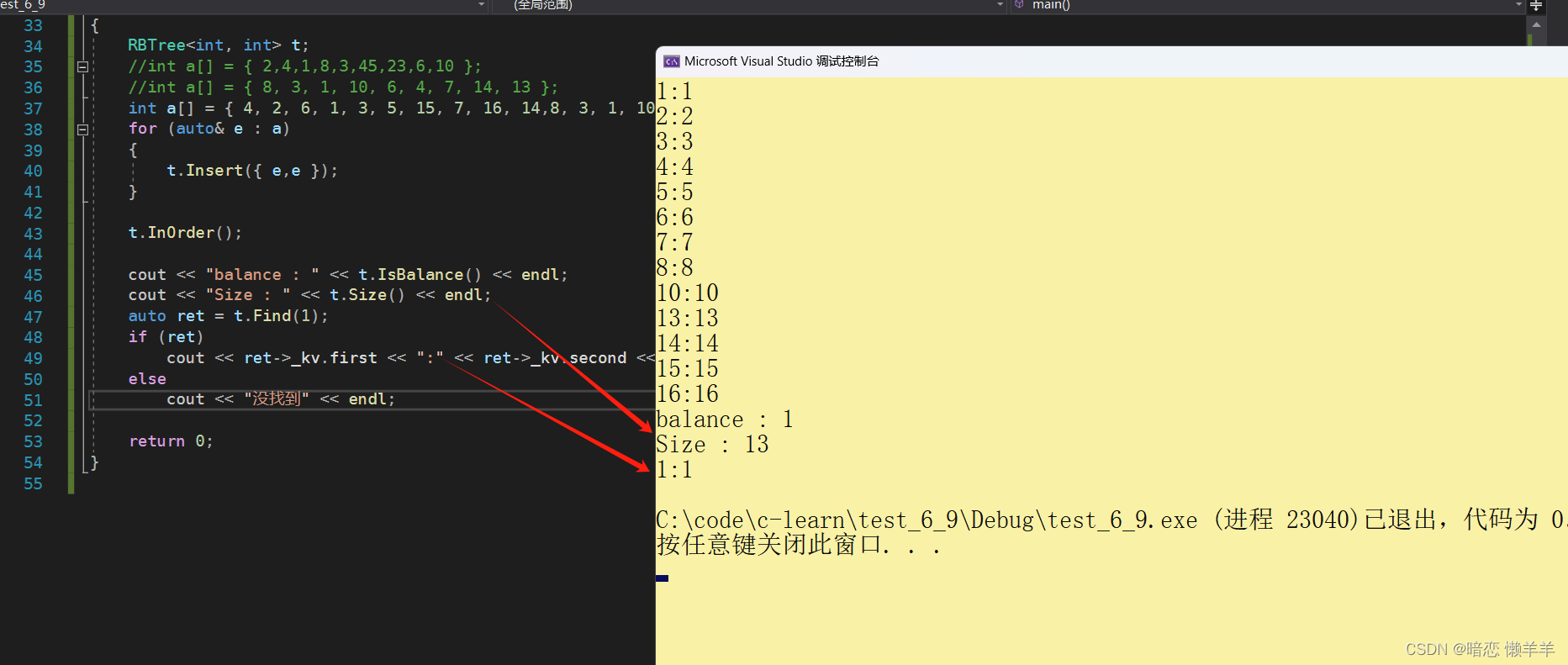
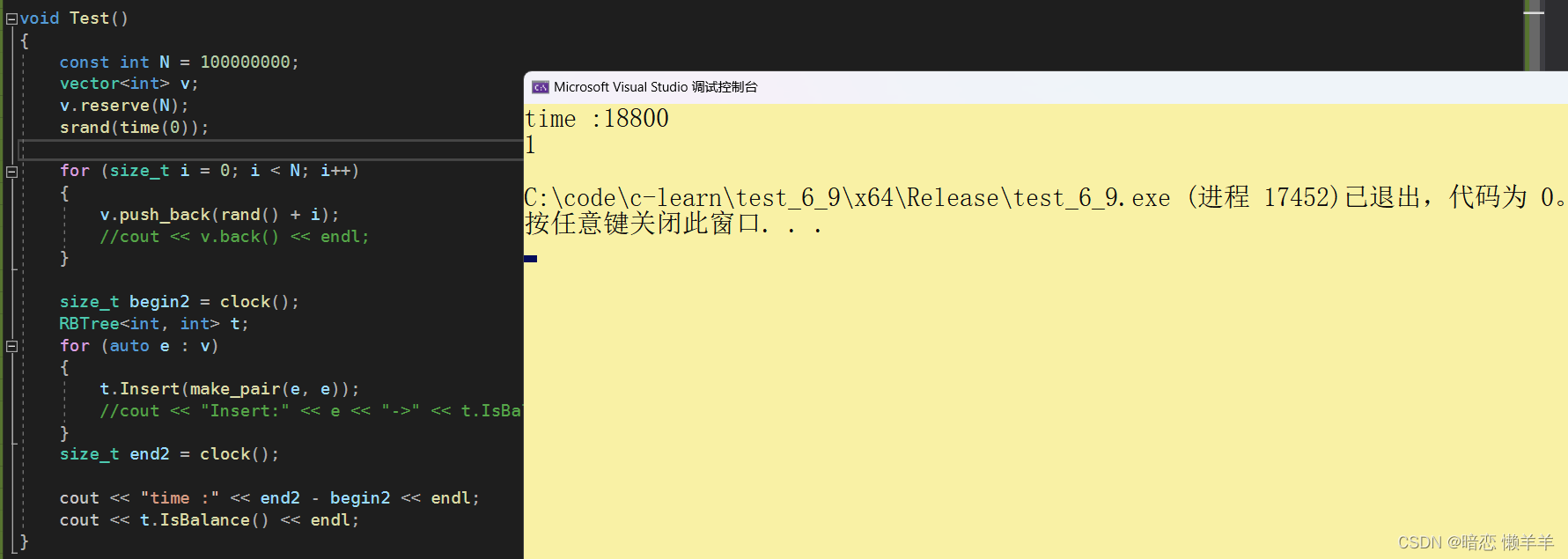
再来一组随机的测试用例：插入1亿个随机值，看看时间和是否平衡（注意这里一亿个节点在32位debug下可能内存空间不够，可以把他改成64的release地址空间大一点）

void Test()
{
	const int N = 100000000;
	vector<int> v;
	v.reserve(N);
	srand(time(0));

	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand() + i);
		//cout << v.back() << endl;
	}

	size_t begin2 = clock();
	RBTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
		//cout << "Insert:" << e << "->" << t.IsBalance() << endl;
	}
	size_t end2 = clock();

	cout << "time :" << end2 - begin2 << endl;
	cout << t.IsBalance() << endl;
}

红黑树的删除：请参考这篇博客 ：红黑树的删除

全部源码

#pragma once

enum Col//颜色
{
	RED,
	BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;//左孩子
	RBTreeNode<K, V>* _right;//右孩子
	RBTreeNode<K, V>* _parent;//父结点
	pair<K, V> _kv;//数据域
	Col _col;//颜色

	RBTreeNode(const pair<K,V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_col(RED)//新插入的节点默认是红色
	{}
};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	RBTree()
		:_root(nullptr)
		,_size(0)
	{}

	bool Insert(const pair<K, V>& kv)
	{
		Node* cur = _root;//当前节点
		Node* parent = nullptr;//插入位置的父亲

		//第一次插入
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_size++;//插入成功节点数+1
			_root->_col = BLACK;//根节点是黑色
			return true;
		}

		//寻找插入的位置
		while (cur)
		{
			if (cur->_kv.first < kv.first)//插入节点的key比当前节点的key大
			{
				parent = cur;
				cur = cur->_right;//去右边找
			}
			else if(cur->_kv.first > kv.first)//插入节点的key比当前节点的key小
			{
				parent = cur;
				cur = cur->_left;//去左边找
			}
			else
			{
				return false;//插入的节点存在
			}
		}

		//找到插入位置
		cur = new Node(kv);
		//链接
		if (parent->_kv.first > cur->_kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		//颜色和高度调整
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)//父亲在爷爷的左
			{
				Node* uncle = grandfather->_right;//叔叔就是父亲的右
				//父亲存在且为红 -> 变色
				if (uncle && uncle->_col == RED)
				{
					grandfather->_col = RED;
					parent->_col = uncle->_col = BLACK;
					//继续向上调整
					cur = grandfather;
					parent = cur->_parent;
				}
				else//叔叔不存在或存在但为黑 -> 变色 + 旋转
				{
					if (cur == parent->_left)//cur在父亲的左
					{
						//		   g
						//	   p		u
						// c
						RotateR(grandfather);//旋转
						parent->_col = BLACK;//变色
						grandfather->_col = RED;
					}
					else//cur在父亲的右
					{
						//		  g
						//	  p		  u
						//        c
						RotateL(parent);//旋转
						RotateR(grandfather);
						cur->_col = BLACK;//变色
						grandfather->_col = RED;
					}

					break;//旋转后不需要再向上更新了
				}
			}
			else//parent在爷爷的右
			{
				Node* uncle = grandfather->_left;//叔叔在父亲的左
				//叔叔存在且为红 -> 变色
				if (uncle && uncle->_col == RED)
				{
					grandfather->_col = RED;
					parent->_col = uncle->_col = BLACK;
					//继续向上调整
					cur = grandfather;
					parent = cur->_parent;
				}
				else//叔叔不存在或存在但为黑 -> 变色 + 旋转
				{
					if (cur == parent->_left)//cur在父亲的左 
					{
						//		  g
						//	  u		   p
						//        c
						RotateR(parent);//旋转
						RotateL(grandfather);
						cur->_col = BLACK;//变色
						grandfather->_col = RED;
					}
					else
					{
						//		  g
						//	  u		   p
						//                 c
						RotateL(grandfather);//旋转
						parent->_col = BLACK;//变色
						grandfather->_col = RED;
					}

					break;//旋转后不需要再向上更新了
				}
			}
		}

		_root->_col = BLACK;//保证根节点永远是黑色
		_size++;//插入成功节点数+1

		return true;
	}

	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)//插入节点的key比当前节点的key大
			{
				cur = cur->_right;//去右边找
			}
			else if (cur->_kv.first > key)//插入节点的key比当前节点的key小
			{
				cur = cur->_left;//去左边找
			}
			else
			{
				return cur;//找到了
			}
		}

		return nullptr;//没找到
	}

	void InOrder()
	{
		return _InOrder(_root);
	}

	size_t Size()
	{
		return _size;
	}

	bool IsBalance()
	{
		if (_root && _root->_col == RED)
		{
			return false;//根为红，一定不是红黑树
		}

		int black = 0;//获取任意一条路径的黑色节点（这里是最左路）
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
			{
				black++;
			}

			cur = cur->_left;
		}

		return Check(_root, black, 0);
	}

private:
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		
		_InOrder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_InOrder(root->_right);
	}
	
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;//父亲的左
		Node* subLR = subL->_right;//左子树的右
		Node* ppNode = parent->_parent;//parent的父节点,方便旋转后的链接

		parent->_left = subLR;//将左子树的右给父亲的做
		if (subLR)
			subLR->_parent = parent;

		subL->_right = parent;//parent做左子树的右
		parent->_parent = subL;

		if (parent == _root)//parent是根
		{
			_root = subL;//此时的新根就是subL
			ppNode = nullptr;
		}
		else//parent不是根
		{
			//将新的根连接到ppNode
			if (ppNode->_left == parent)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;//父亲的右
		Node* subRL = subR->_left;//右子树的左
		Node* ppNode = parent->_parent;//parent的父节点,方便旋转后的链接

		parent->_right = subRL;//将右子树的左连接到parent的右
		if (subRL)
			subRL->_parent = parent;

		subR->_left = parent;//parent连接到subR的左
		parent->_parent = subR;

		if (parent == _root)//parent是根
		{
			_root = subR;//此时的新根就是subR
			ppNode = nullptr;
		}
		else//parent不是根
		{
			//将新的根连接到ppNode
			if (ppNode->_left == parent)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}
	}

	bool Check(Node* root, const int black, int num)
	{
		if (root == nullptr)
		{
			//当走到叶子节点的时候和其他路径的黑色节点的个数不一样
			if (black != num)
			{
				return false;
			}

			return true;
		}

		//存在连续的红色节点
		if (root->_col == RED && root->_parent && root->_parent->_col == RED)
		{
			cout << root->_kv.first << " ：存在连续的红色节点" << endl;
			return false;
		}

		//遇到黑色节点++
		if (root->_col == BLACK)
		{
			num++;
		}

		//当前节点符合红黑树，它的左右子树也要都符合
		return Check(root->_left, black, num) && Check(root->_right, black, num);
	}


private:
	Node* _root;//根节点
	size_t _size;//节点的数量
};

红黑树的效率分析以及应用

红黑树和AVL树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(log_2 N)，红黑树不追 求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数， 所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

红黑树的应用

C++的STL库中的map/set/multimap/multiset底层都是红黑树实现的

一些Java的库；例如: TreeMap和TreeSet等

一些Linux的内核，例如：进程调度等

OK，本期分享就到这里，好兄弟，我们下期再见！

结束语：简单的事重复做，重复的是坚持做！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1806759.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java SE(Java Platform, Standard Edition)

Java SE(Java Platform, Standard Edition)

Java SE&#xff08;Java Platform, Standard Edition&#xff09; 是Java平台的一个版本&#xff0c;面向桌面应用程序、服务器和嵌入式环境。Java SE提供了开发和运行Java应用程序的基础API&#xff08;Application Programming Interface&#xff0c;应用程序编程接口&…
阅读更多...
Docker之路（三）docker安装nginx实现对springboot项目的负载均衡

Docker之路（三）docker安装nginx实现对springboot项目的负载均衡

Docker之路&#xff08;三&#xff09;dockernginxspringboot负载均衡 前言&#xff1a;一、安装docker二、安装nginx三、准备好我们的springboot项目四、将springboot项目分别build成docker镜像五、配置nginx并且启动六、nginx的负载均衡策略七、nginx的常用属性八、总结 前言…
阅读更多...
【leetcode--盛水最多的容器】

【leetcode--盛水最多的容器】

给定一个长度为 n 的整数数组 height 。有 n 条垂线&#xff0c;第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线&#xff0c;使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 写出来了一半&#xff0c;想到用双指针&am…
阅读更多...
大数据数仓的数据回溯

大数据数仓的数据回溯

在大数据领域&#xff0c;数据回溯是一项至关重要的任务&#xff0c;它涉及到对历史数据的重新处理以确保数据的准确性和一致性。 数据回溯的定义与重要性 数据回溯&#xff0c;也称为数据补全&#xff0c;是指在数据模型迭代或新模型上线后&#xff0c;对历史数据进行重新处理…
阅读更多...
VisionPro的应用和入门教程

VisionPro的应用和入门教程

第1章 关于VisionPro 1.1 康耐视的核心技术 1. 先进的视觉系统 康耐视的视觉系统结合了高性能的图像传感器、复杂的算法和强大的计算能力&#xff0c;能够实时捕捉、分析和处理高分辨率图像。其视觉系统包括固定式和手持式两种&#xff0c;适用于各种工业环境。无论是精密电…
阅读更多...
centos7安装字体

centos7安装字体

1.安装命令 yum install fontconfig #字体库命令 yum install mkfontscale #更新字体命令2.安装字体&#xff08;注意权限问题&#xff09; 进入目录 /usr/share/fonts &#xff0c;该目录是 centos7 字体库的默认安装目录。在该目录下创建一个文件夹 ekp &#xff08;名字…
阅读更多...
C++从入门到精通（最详细教程，12万总结，带你掌握c++知识，涵盖大量知识点）

C++从入门到精通（最详细教程，12万总结，带你掌握c++知识，涵盖大量知识点）

目录 一、面向对象的思想 二、类的使用 1.类的构成 2.类的设计 三、对象的基本使用 四、类的构造函数 1.构造函数的作用 2.构造函数的特点 3.默认构造函数 3.1.合成的默认构造函数 3.2.手动定义的默认构造函数 四、自定义的重载构造函数 五、拷贝构造函数 1.手动…
阅读更多...
312. 戳气球 Hard

312. 戳气球 Hard

有 n 个气球&#xff0c;编号为0 到 n - 1&#xff0c;每个气球上都标有一个数字&#xff0c;这些数字存在数组 nums 中。 现在要求你戳破所有的气球。戳破第 i 个气球&#xff0c;你可以获得 nums[i - 1] * nums[i] * nums[i 1] 枚硬币。 这里的 i - 1 和 i 1 代表和 i 相邻…
阅读更多...
设计模式之观察者模式ObserverPattern（十一）

设计模式之观察者模式ObserverPattern（十一）

一、概述 观察者模式 (Observer Pattern) 是一种行为型设计模式&#xff0c;又被称为发布-订阅 (Publish/Subscribe) 模式&#xff0c;它定义了对象之间的一种一对多的依赖关系&#xff0c;使得当一个对象的状态发生变化时&#xff0c;所有依赖于它的对象都会自动收到通知并更新…
阅读更多...
Sui Generis如何为艺术家弥合Web3的鸿沟

Sui Generis如何为艺术家弥合Web3的鸿沟

Sui Generis是一家于3月推出的NFT拍卖行&#xff0c;其联合创始人兼CEO Gab9说其愿景是——更好、更大、更强&#xff01; 表面上看&#xff0c;Sui Generis是备受欢迎的Tombheads NFT拍卖行的重新品牌化&#xff0c;该拍卖行今年早些时候从Fantom区块链迁移出来。但它于3月31…
阅读更多...
Ajax 快速入门

Ajax 快速入门

Ajax 概念&#xff1a;Ajax是一种Web开发技术&#xff0c;允许在不重新加载整个页面的情况下&#xff0c;与服务器交换数据并更新网页的部分内容。 作用&#xff1a; 数据交换&#xff1a;Ajax允许通过JavaScript向服务器发送请求&#xff0c;并能够接收服务器响应的数据。 异…
阅读更多...
从GAN到WGAN（01/2）

从GAN到WGAN（01/2）

从GAN到WGAN 文章目录 一、说明二、Kullback-Leibler 和 Jensen-Shannon 背离三、生成对抗网络 &#xff08;GAN&#xff09;四、D 的最优值是多少&#xff1f;五、什么是全局最优&#xff1f;六、损失函数代表什么&#xff1f;七、GAN中的问题 一、说明 生成对抗网络 &#…
阅读更多...
开源项目学习——vnote

开源项目学习——vnote

一、介绍 vnote是一款免费且开源的markdown编辑器&#xff0c;用C开发&#xff0c;基于Qt框架&#xff0c;windows/linux/mac都能用。 二、编译 $ git clone --recursive https://github.com/vnotex/vnote.git $ cd vnote && mkdir build $ cd build $ cmake ../ $ …
阅读更多...
【端午安康，给大家讲个“网络”故事，深刻一下！】

【端午安康，给大家讲个“网络”故事，深刻一下！】

牛马我&#x1f434;上周又挨锤了&#xff0c; 网络是不稳定的&#xff0c;博学多知的你可能知道&#xff0c;可能不知道。但假如没亲身经历过&#xff0c;知不知道都不深刻&#xff0c;牛马踩了个网络的坑&#xff0c;深刻了&#xff0c;这里分享下&#xff0c; 一个真相 无…
阅读更多...
【算法训练记录——Day27】

【算法训练记录——Day27】

Day27——回溯算法Ⅲ 1.组合总和2.组合总和II3.分割回文串 内容 ● 39.组合总和 ● 40.组合总和II ● 131.分割回文串 1.组合总和 思路&#xff1a;和组合总和一样&#xff0c;先从candidates中遍历选择元素&#xff0c;但是纵向递归时所选择元素要包括当前元素 vector<int&…
阅读更多...
289M→259M得物包体积治理实践

289M→259M得物包体积治理实践

一、前言 iOS应用的包体积大小是衡量得物性能的重要指标&#xff0c;过大包体积会降低用户对应用的下载意愿&#xff0c;还会增加用户的下载等待时间以及用户手机的存储空间&#xff0c;本文重点介绍在包体积治理中的新思路以及原理与实践。 二、原理介绍 Macho产物测试 我…
阅读更多...
什么是档案数字化管理

什么是档案数字化管理

档案数字化管理指的是将传统的纸质档案转换为数字形式&#xff0c;并通过电子设备、软件和网络技术进行管理和存储的过程。 档案数字化管理包括以下几个步骤&#xff1a; 1. 扫描和数字化&#xff1a;将纸质档案通过扫描仪转换为数字图像或文档。可以使用OCR&#xff08;光学字…
阅读更多...
AI论文速读 | 2024[ICML]FlashST：简单通用的流量预测提示微调框架

AI论文速读 | 2024[ICML]FlashST：简单通用的流量预测提示微调框架

题目&#xff1a; FlashST: A Simple and Universal Prompt-Tuning Framework for Traffic Prediction 作者&#xff1a;Zhonghang Li, Lianghao Xia&#xff08;夏良昊&#xff09;, Yong Xu&#xff08;徐勇&#xff09;, Chao Huang 机构&#xff1a;华南理工大学&#xf…
阅读更多...
搜索与图论：深度优先搜索

搜索与图论：深度优先搜索

搜索与图论&#xff1a;深度优先搜索 题目描述参考代码 题目描述 参考代码 #include <iostream>using namespace std;const int N 10;int n; int path[N]; bool st[N];void dfs(int u) {// u n 搜索到最后一层if (u n){for (int i 0; i < n; i) printf("%d …
阅读更多...
C++ MPI多进程并发

C++ MPI多进程并发

下载 用法 mpiexec -n 8 $PROCESS_COUNT x64\Debug\$TARGET.exe 多进程并发启动 mpiexec -f hosts.txt -n 3 $PROCESS_COUNT x64\Debug\$TARGET.exe 联机并发进程&#xff0c;其它联机电脑需在相同路径下有所有程序 //hosts.txt 192.168.86.16 192.168.86.123 192.168…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023