DS：堆的结构与实现

news2024/11/24 5:33:09

欢迎来到Harper.Lee的学习世界！
博主主页传送门：Harper.Lee的博客主页
想要一起进步的uu可以来后台找我哦！

一、堆的概念与结构

1.1 堆的概念

堆（Heap）是完全二叉树中的一种，分为大根堆和小根堆。
特点：1.每个节点的值都大于或等于其左右孩子节点的值，称为大根堆；或是每个节点的值都小于或等于其左右孩子的值，称为小根堆。2.从堆的概念不难看出，大根堆堆顶为集合的最大值，小根堆堆顶为集合的最小值。（注意：父亲与孩子之间有大小关系，但是兄弟之间没有大小关系，因此堆并不是有序的！！！）

1.2 堆的结构

根据上一节（DS：树与二叉树的相关概念）可知，完全二叉树以数组的形式存储，因此堆采用数组的形式进行数据的存储。
父子的下标特点：(1)父亲找孩子：leftchild=parent2+1，rightchild=parent2+2；(2)孩子找父亲：parent=（child-1）/2。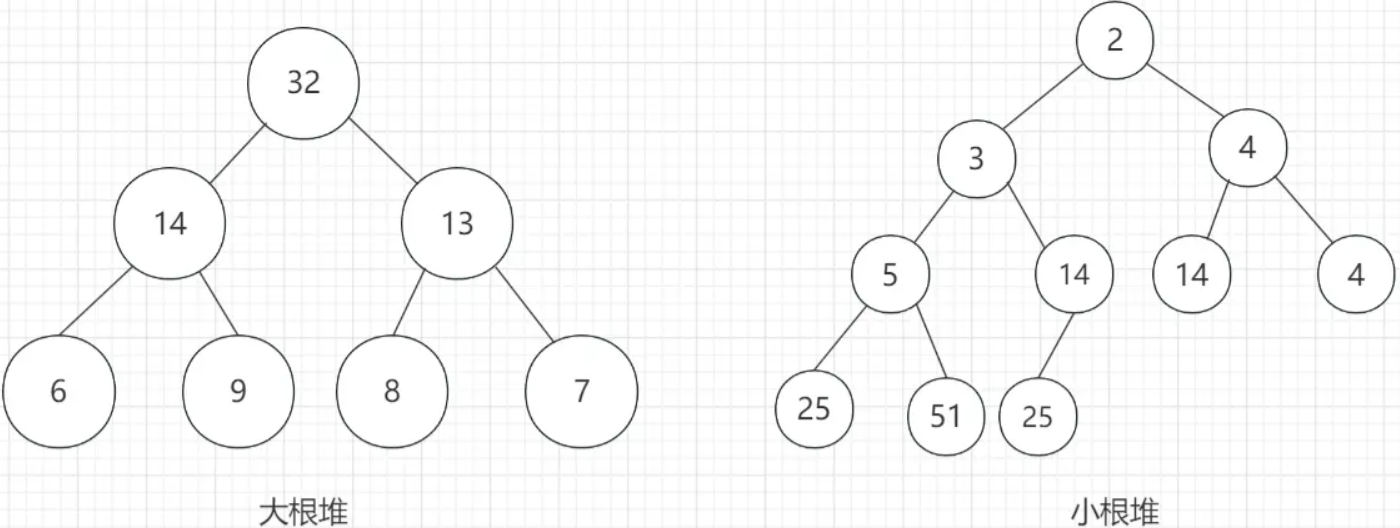
image.png

二、堆的实现

2.0 分析过程

插入数据部分分析过程：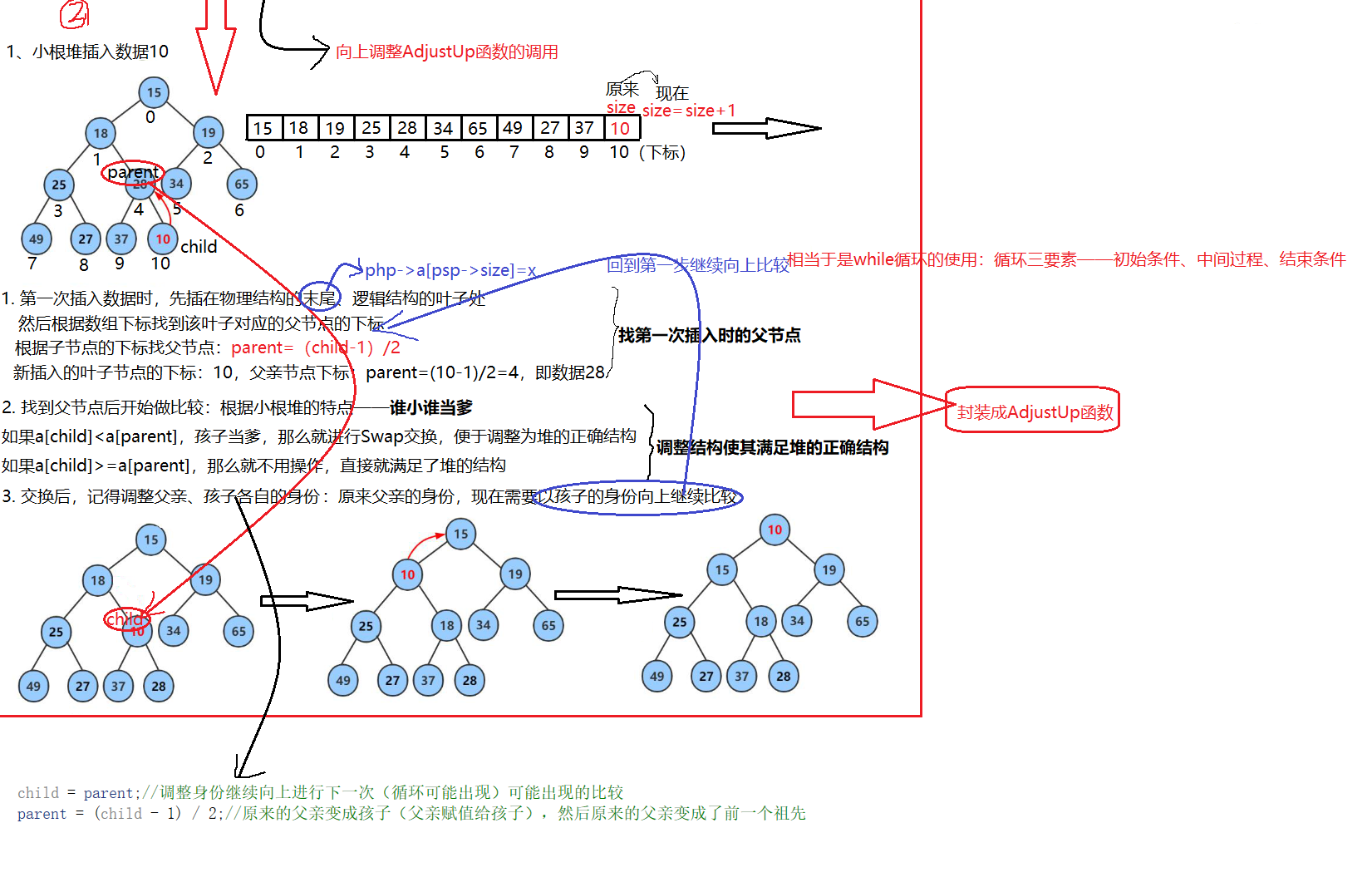
image.png

2.1 堆的相关结构体的创建

堆的底层是数组，因此结构体就以数组的形式创建。这一步和之前顺序表的创建基本一样。

//结构体的创建
typedef int HPDataType;
typedef struct Heap
{
    //以数组为背景
    HPDataType* a;
    int size;//表示存储的数据个数
    int capacity;//表示空间容量，因为我么虽然操作的是二叉树
}HP;

2.2 堆的初始化

//初始化
void HPInit(HP* php)
{
	//Q：这里需要断言吗？？?  A：php需要断言,避免传入空堆
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;//可以给值，也可以不给值（前面有讲过）
	//如果capacity和size不给值的话，在插入数据的时候就需要动态申请开辟空间
	//如果capacity和size赋值的话，就是另外的一种操作。
}

2.3 堆的插入

push就有建立堆的功能。一边插入数据，一边调整出堆的结构。

//push堆的操作
void HPPush(HP* php,HPDataType x)//传入堆，插入一个数据x
{
	assert(php);

	//1. 先判断空间是否足够
	//1. 若空间不够（说明之前有空间的，即使没有空间，capacity也等于size），则进行增容操作
	if (php->capacity == php->size)//if (php->capacity == php->size == 0)，而不是判断是否为空
	{

		int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("malloc fail");
			exit(1);//return;//直接返回也可
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	//2. 开始插入数据
	php->a[php->size] = x;//
	php->size++;

	//3. 调用向上调整函数
	AdjustUp(php->a, php->size-1);//为什么第2个参数是size-1而不是size?----要弄清楚size的位置：最后一个数据位置的下标+1
}

2.4 向上调整算法

//向上调整函数的定义
void AdjustUp(HPDataType* a, int child)//从child的位置开始调整，现在child就是数组末尾了
{
	//虽然控制的十足，但是要把它想象成实在控制二叉树（堆）
	//1.第一次插入的数据在数组的末尾child位置
	int parent = (child - 1) / 2;//父节点的位置找到了
	//2.开始比较父节点和子节点--小根堆：谁小谁当爹
	//循环三要素：a.初始条件b.中间过程c.结束条件
	/*while (a[parent] >= 0)//为什么循环结构是>=0?因为实际上最初始的child从末尾开始就需要和她的所有祖先（一条线上的）全部进行比较，比较完循环才会结束）*/
	//如果用parent>=0来判断，那么由于（0-1）/2是-1/2，取整后还是0，就会再次进入循环，一般情况来说这是错误的，但是这里出现了一个巧合：parent==child==0，break跳出循环了，程序歪打正着的正确了。

	while (a[child] > 0)//上面的循环条件写成下面这种会更好
	{  
		if (a[child] < a[parent])
		{
			//3.开始进行交换操作（Swap函数的调用）
			Swap(&a[child], &a[parent]);
			child = parent;//调整身份继续向上进行下一次（循环可能出现）可能出现的比较
			parent = (child - 1) / 2;//原来的父亲变成孩子（父亲赋值给孩子），然后原来的父亲变成了前一个祖先。
		}
		else
		{
			break;// 满足小根堆的结构
		}
	}
}

2.5 交换函数

//Swap函数的调用
void Swap(HPDataType* a, HPDataType* b)
{
	HPDataType tmp;
	tmp = *a;
	*a = *b;
	*b = tmp;
}

2.6 堆的删除

删除堆的末尾数据是没意义的，因为这个操作很简单，封装成函数就是小题大做了。因此，我们一般删除的是堆顶数据即根位置的数据。但是，如果直接删除/挪动/覆盖了堆顶数据，可能父子关系、叔侄关系、兄弟关系会乱套，倒反天罡了。
所以我么选择一种新的解决办法：根节点的数据和尾节点的数据进行交换，然后再删除尾节点的数据，然后进行向下调整算法重新调整堆的结构，这样就实现了堆顶元素的删除。

分析过程如下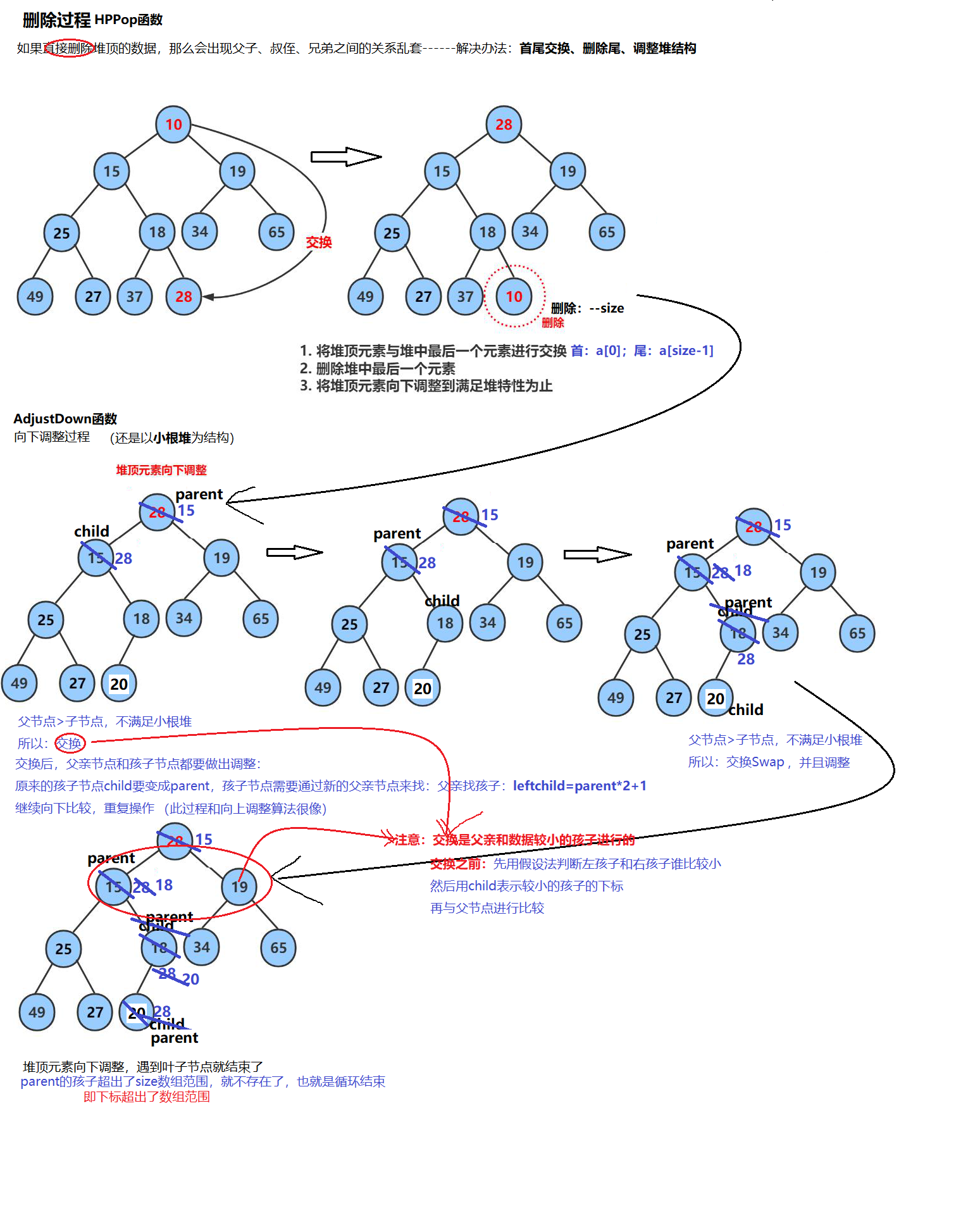：image.png
代码实现：

//Pop删除数据——要求删除堆顶即根位置的数据，删除末尾数据没有意义
void HPPop(HP* php)
{
	assert(php);
	//1.将堆顶元素和最后一个元素进行交换
	Swap(&php->a[php->size-1], &php->a[0]);//尾元素：a[size-1]
	//2.删除堆中的最后一个元素的数据---怎么删啊?---删除数组中最后一个元素的数据
	//free(php->a[php->size-1]);//不能使用free，因为内存申请的空间必须一块儿释放，而不是一部分一部分地释放的
	php->size--;//php->size -= 1;
	//3.向下调整算法的运用
	AdjustDown(php->a, php->size, 0);
}

Q1：删除堆顶数据有什么意义或者作用呢？

删除掉了目前堆里最小的元素，相当于取出来堆中的最小的元素。如果连续使用HPPop函数，那么就可以从小到大依次取出堆中的数据，这就是简单模式的TOP-K。

Q2：HPPop的时间复杂度是多少？

pop的时间复杂度为logN（最坏情况），O(1)（最好情况）。而满二叉树/完全二叉树的树高就是logN。

应用：可以一边HPTop获取堆中目前的最小的数据，然后HPPop删除掉这个数据，这样就可以进行排序打印了。

2.7 向下调整算法

//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent)//从parent根节点开始调整
{
	//1.先确定（假设法）用哪个孩子与父亲做比较
	//假设左孩子比右孩子小
	int child = parent * 2 + 1;//根据父节点找到子节点
	while (child < n)//child>=n时，说明该孩子已经不存在了 
	{
		//找出小的孩子
		//if (a[child + 1] < a[child])//此写法存在风险：左孩子<n没有风险，但是右孩子+1就可能存在风险
		if (child + 1 < n && a[child + 1] < a[child])
		{
			//如果右孩子比左孩子小：假设不成立，修改假设的内容：
			++child;//child右移变成右孩子
		}
		//2.小孩子与父亲做比较
		if (a[child] < a[parent])
		{
			Swap(&a[parent], &a[child]);
			//3.交换后进行父亲与孩子的调整
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

2.8 获取堆顶的数据

//获取堆顶的数据（返回堆顶元素）
HPDataType HPTop(HP* php)//top-k问题
{
	//断言：
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

2.9 判空

//判空
bool HPEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

2.10 堆的销毁

//销毁
void HPDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->capacity = php->size = 0;
	php->a == NULL;
}

2.11 前k个元素的打印

main函数中堆的建立过程以及打印实现过程：

//
int main()
{
   int a[] = { 4,2,8,1,5,6,9,7 };//这个数组现在还不是堆，需要将其变成一个堆（一个个地去插入）
	HP hp;//1.创建一个堆hp
	//2.初始化
	HPInit(&hp);
	//3.建堆（需要插入多个数据，因此，需要多次调用HPPush函数，使用循环结构）
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HPPush(&hp, a[i]);//建堆的同时 调整了堆的结构
	}
	//4.打印堆中的所有数据
	//while (!HPEmpty(&hp))
	//{
	//	printf("%d ", HPTop(&hp));//获取到堆顶的数据
	//	HPPop(&hp);
	//}
	//5.如果是找堆里的最大的前k个数据
	int k = 0;
	scanf("%d", &k);
	while (k--)
	{
		printf("%d ", HPTop(&hp));
		HPPop(&hp);
	}
	printf("\n");
    HPDestroy(&hp); 
    return 0;
}

这里是实现了打印上的有序，但是数组本身并不有序。我们可以将每次HPTop操作获得的堆顶数据放在a数组中，就可以使得数组有序了。也就是上一段代码中注释掉的第 4. 点

	//4.打印堆中的所有数据
	//while (!HPEmpty(&hp))
	//{
	//	printf("%d ", HPTop(&hp));//获取到堆顶的数据
	//	HPPop(&hp);
	//}
    //6. 数组a有序的改变
    int i = 0;
	while (!HPEmpty(&hp))
	{
		//printf("%d ", HPTop(&hp));//获取到堆顶的数据
		a[i++] = HPTop(&hp);
		HPPop(&hp);
	}

三、堆的实现-全部代码

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>



//本次-----堆的实现过程 —— 框架

//1. 结构体的创建
typedef int HPDataType;
typedef struct Heap
{
	//以数组为背景
	HPDataType* a;
	int size;//表示存储的数据个数
	int capacity;//表示空间容量，因为我么虽然操作的是二叉树
}HP;

//2. 初始化和销毁
void HPInit(HP* php);//php是结构体指针变量
void HPDestroy(HP* php);
//3. 插入HPDataType类型数据x（节点），注意保持堆的完整结构
void HPPush(HP* php, HPDataType x);
//4. Pop删除数据——要求删除堆顶即根位置的数据
void HPPop(HP* php); 
//5. 向下调整法
void AdjustUp(HPDataType* a,int child);
//6. 向上调整法
void AdjustDown(HPDataType* a, int n, int parent);
//7. 判断堆结构是否为空
bool HPEmpty(HP* php);
//8. 交换函数
void Swap(HPDataType* a, HPDataType* b);
//9. 获取堆顶数据
HPDataType HPTop(HP* php);


#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

//（1） 初始化
void HPInit(HP* php)//传入堆（php是堆的名称）
{
	//Q：这里需要断言吗？？?  A：php需要断言,避免传入空堆
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;//可以给值，也可以不给值（前面有讲过）
	//如果capacity和size不给值的话，在插入数据的时候就需要动态申请开辟空间
	//如果capacity和size赋值的话，就…………？？？两种玩法一样
}

//（2） 销毁（free释放掉动态申请的空间）
void HPDestroy(HP* php)
{
	assert(php);
	free(php);//释放掉空间后记得善后
	php->capacity = php->size = 0;
	php->a = NULL;
}

//（5）Swap函数的调用
void Swap(HPDataType* a, HPDataType* b)
{
	HPDataType tmp;
	tmp = *a;
	*a = *b;
	*b = tmp;
}

//（4） 向上调整函数的定义
void AdjustUp(HPDataType* a, int child)//从child的位置开始调整，现在child就是数组末尾了
{
	//虽然控制的十足，但是要把它想象成实在控制二叉树（堆）
	//1.第一次插入的数据在数组的末尾child位置
	int parent = (child - 1) / 2;//父节点的位置找到了
	//2.开始比较父节点和子节点--小根堆：谁小谁当爹
	//循环三要素：a.初始条件b.中间过程c.结束条件
	/*while (a[parent] >= 0)//为什么循环结构是>=0?因为实际上最初始的child从末尾开始就需要和她的所有祖先（一条线上的）全部进行比较，比较完循环才会结束）*/
	//如果用parent>=0来判断，那么由于（0-1）/2是-1/2，取整后还是0，就会再次进入循环，一般情况来说这是错误的，但是这里出现了一个巧合：parent==child==0，break跳出循环了，程序歪打正着的正确了。

	while (a[child] > 0)//上面的循环条件写成下面这种会更好
	{  
		if (a[child] < a[parent])
		{
			//3.开始进行交换操作（Swap函数的调用）
			Swap(&a[child], &a[parent]);
			child = parent;//调整身份继续向上进行下一次（循环可能出现）可能出现的比较
			parent = (child - 1) / 2;//原来的父亲变成孩子（父亲赋值给孩子），然后原来的父亲变成了前一个祖先。
		}
		else
		{
			break;// 满足小根堆的结构
		}
	}
}

//（3） push堆的操作
void HPPush(HP* php,HPDataType x)//传入堆，插入一个数据x
{
	assert(php);

	//1. 先判断空间是否足够
	//1. 若空间不够（说明之前有空间的，即使没有空间，capacity也等于size），则进行增容操作
	if (php->capacity == php->size)//if (php->capacity == php->size == 0)，而不是判断是否为空
	{

		int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("malloc fail");
			exit(1);//return;//直接返回也可
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	//2. 开始插入数据
	php->a[php->size] = x;//
	php->size++;

	//3. 调用向上调整函数
	AdjustUp(php->a, php->size-1);//为什么第2个参数是size-1而不是size?----要弄清楚size的位置：最后一个数据位置的下标+1
}

//（7）向下调整算法
void AdjustDown(HPDataType* a, int n, int parent)//从parent根节点开始调整
{
	//1.先确定（假设法）用哪个孩子与父亲做比较
	//假设左孩子比右孩子小
	int child = parent * 2 + 1;//根据父节点找到子节点
	while (child < n)//child>=n时，说明该孩子已经不存在了 
	{
		//找出小的孩子
		//if (a[child + 1] < a[child])//此写法存在风险：左孩子<n没有风险，但是右孩子+1就可能存在风险
		if (child + 1 < n && a[child + 1] < a[child])
		{
			//如果右孩子比左孩子小：假设不成立，修改假设的内容：
			++child;//child右移变成右孩子
		}
		//2.小孩子与父亲做比较
		if (a[child] < a[parent])
		{
			Swap(&a[parent], &a[child]);
			//3.交换后进行父亲与孩子的调整
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//（6）Pop删除数据——要求删除堆顶即根位置的数据，删除末尾数据没有意义
void HPPop(HP* php)//logN
{
	assert(php);
	assert(php->size > 0);
	//1.将堆顶元素和最后一个元素进行交换
	Swap(&php->a[php->size-1], &php->a[0]);//尾元素：a[size-1]
	//2.删除堆中的最后一个元素的数据---怎么删啊?---删除数组中最后一个元素的数据
	//free(php->a[php->size-1]);//不能使用free，因为内存申请的空间必须一块儿释放，而不是一部分一部分地释放的
	php->size--;//php->size -= 1;
	//3.向下调整算法的运用
	AdjustDown(php->a, php->size, 0);
}

//（7）获取堆顶的数据（返回堆顶元素）
HPDataType HPTop(HP* php)//top-k问题
{
	//断言：
	assert(php);
	assert(php->size > 0);//作用？？
	return php->a[0];
}
//（8）判空
bool HPEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}



#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

int main()
{ 
	int a[] = { 4,2,8,1,5,6,9,7 };//这个数组现在还不是堆，需要将其变成一个堆（一个个地去插入）
	HP hp;//1.创建一个堆hp
	//2.初始化
	HPInit(&hp);
	//3.建堆（需要插入多个数据，因此，需要多次调用HPPush函数）
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HPPush(&hp, a[i]);//建堆的同时 调整了堆的结构
	}
	//1. 打印堆中的所有数据
	//while (!HPEmpty(&hp))
	//{
	//	printf("%d ", HPTop(&hp));//获取到堆顶的数据
	//	HPPop(&hp);
	//}
	//如果是找堆里的最大的前k个数据
	int k = 0;
	scanf("%d", &k);
	while (k--)
	{
		printf("%d ", HPTop(&hp));
		HPPop(&hp);
	}
	printf("\n");

	return 0;
}

喜欢的uu记得三连支持哦！
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1806450.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【RAG入门教程03】Langchian框架-文档加载

【RAG入门教程03】Langchian框架-文档加载

Langchain 使用文档加载器从各种来源获取信息并准备处理。这些加载器充当数据连接器&#xff0c;获取信息并将其转换为 Langchain 可以理解的格式。 LangChain 中有几十个文档加载器&#xff0c;可以在这查看https://python.langchain.com/v0.2/docs/integrations/document_lo…
阅读更多...
BabylonJS 6.0文档 Deep Dive 动画（四）：通过动画排序制作卡通片

BabylonJS 6.0文档 Deep Dive 动画（四）：通过动画排序制作卡通片

一种最为直接的方法是为每个动画剪辑&#xff08;Animatin Clip&#xff09;指定开始时间&#xff0c;最终形成一个卡通动画&#xff08;Cartoon&#xff09;。 1. 设计 1.1 概述 动画的脚本如下&#xff1a; 摄像机显示了一栋带门的建筑物。摄像机靠近门并停止。门打开&am…
阅读更多...
【数据结构】队列——循环队列（详解）

【数据结构】队列——循环队列（详解）

目录 0 循环队列 1 特定条件下循环队列队/空队满判断条件 1.1 队列为空的条件 1.2 队列为满的条件 2 循环队列的实现 3 示例 4 注意事项 0 循环队列 循环队列&#xff08;Circular Queue&#xff09;是队列的一种实现方式&#xff0c;它通过将队列存储空间的最后一…
阅读更多...
高考后的职业规划：学习LabVIEW开发前景广阔

高考后的职业规划：学习LabVIEW开发前景广阔

在今天的高考后&#xff0c;选择学习LabVIEW开发为未来职业规划将大有可为。LabVIEW以其图形化编程、强大的数据处理和硬件集成功能&#xff0c;广泛应用于工程、科研、自动化测试等领域。掌握LabVIEW开发技能&#xff0c;不仅就业前景广阔&#xff0c;还能参与前沿技术应用&am…
阅读更多...
Linux云计算架构师涨薪班课程内容包含哪些？

Linux云计算架构师涨薪班课程内容包含哪些？

第一阶段&#xff1a;Linux云计算运维初级工程师 目标 云计算工程师&#xff0c;Linux运维工程师都必须掌握Linux的基本功&#xff0c;这是一切的根本&#xff0c;必须全部掌握&#xff0c;非常重要&#xff0c;有了这些基础&#xff0c;学习上层业务和云计算等都非常快&#x…
阅读更多...
ToonCrafter - AI 生成动画越来越简单了，两张照片生成动画视频 本地一键整合包

ToonCrafter - AI 生成动画越来越简单了，两张照片生成动画视频 本地一键整合包

动画制作对很多人来说应该都是一项非常专业且复杂的工作&#xff0c;需要学习专门的知识&#xff0c;掌握特定的工具&#xff0c;并且投入大量的时间精力才能得到成果&#xff0c;不过最近出现的一款 AI 动画制作工具 ToonCrafter 则有希望改变这一现状。它只需 2 张图像就生成…
阅读更多...
Web3设计风格和APP设计风格

Web3设计风格和APP设计风格

Web3设计风格和传统APP设计风格在视觉和交互设计上有一些显著的区别。这些差异主要源于Web3技术和理念的独特性&#xff0c;以及它们在用户体验和界面设计中的具体应用。以下是Web3设计风格与传统APP设计风格的主要区别。北京木奇移动技术有限公司&#xff0c;专业的软件外包开…
阅读更多...
未在本地计算机上注册“Microsoft.ACE.OLEDB.12.0”提供程序。.net 读取excel的时候报错（实测有效）

未在本地计算机上注册“Microsoft.ACE.OLEDB.12.0”提供程序。.net 读取excel的时候报错（实测有效）

1. 下载AccessDatabaseEngine.exe 下载链接 添加链接描述 2. office excel是64为的需要安装【AccessDatabaseEngine.exe】、32位的【AccessDatabaseEngine_X64.exe】 3. 我的是64为&#xff0c;跳过32位安装检测 1. 找到下载的安装包 2.输入安装包文件全称并在后面加上/pas…
阅读更多...
ctfshow-web入门-命令执行（web29）五种解法绕过文件名检测

ctfshow-web入门-命令执行（web29）五种解法绕过文件名检测

命令执行&#xff0c;需要严格的过滤 进入 php 代码审计了&#xff1a; 第一题代码很简单&#xff0c;就是对 preg_match 绕过&#xff0c;只要提交的参数值不出现 flag 就行 先看一下当前目录下的文件&#xff0c;构造 payload&#xff1a; ?csystem(ls); 可以看到 flag 就…
阅读更多...
电感十大供应商

电感十大供应商

电感品牌-电感器品牌排行榜-电感十大品牌-Maigoo品牌榜
阅读更多...
小柴带你学AutoSar系列一、基础知识篇（5）makefile基础

小柴带你学AutoSar系列一、基础知识篇（5）makefile基础

Flechazohttps://www.zhihu.com/people/jiu_sheng 小柴带你学AutoSar总目录https://blog.csdn.net/qianshang52013/article/details/138140235?spm=1001.2014.3001.5501
阅读更多...
Python基础——字符串

Python基础——字符串

一、Python的字符串简介 Python中的字符串是一种计算机程序中常用的数据类型【可将字符串看作是一个由字母、数字、符号组成的序列容器】&#xff0c;字符串可以用来表示文本数据。 通常使用一对英文的单引号&#xff08;&#xff09;或者双引号&#xff08;"&#xff09;…
阅读更多...
电子电气架构 ---车载安全防火墙

电子电气架构 ---车载安全防火墙

我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 屏蔽力是信息过载时代一个人的特殊竞争力，任何消耗你的人和事，多看一眼都是你的不对。非必要不费力证明自己，无利益不试图说服别人，是精神上的节…
阅读更多...
docker——基础知识

docker——基础知识

简介 一、什么是虚拟化和容器化 ​ 实体计算机叫做物理机&#xff0c;又时也称为寄主机&#xff1b; ​ 虚拟化&#xff1a;将一台计算机虚拟化为多态逻辑计算机&#xff1b; ​ 容器化&#xff1a;一种虚拟化技术&#xff0c;操作系统的虚拟化&#xff1b;将用户空间软件实…
阅读更多...
【数据结构】 -- 堆 （堆排序）（TOP-K问题）

【数据结构】 -- 堆 （堆排序）（TOP-K问题）

引入 要学习堆&#xff0c;首先要先简单的了解一下二叉树&#xff0c;二叉树是一种常见的树形数据结构&#xff0c;每个节点最多有两个子节点&#xff0c;通常称为左子节点和右子节点。它具有以下特点&#xff1a; 根节点&#xff08;Root&#xff09;&#xff1a;树的顶部节…
阅读更多...
为什么Kubernetes（K8S）弃用Docker：深度解析与未来展望

为什么Kubernetes（K8S）弃用Docker：深度解析与未来展望

为什么Kubernetes弃用Docker&#xff1a;深度解析与未来展望 &#x1f680; 为什么Kubernetes弃用Docker&#xff1a;深度解析与未来展望摘要引言正文内容&#xff08;详细介绍&#xff09;什么是 Kubernetes&#xff1f;什么是 Docker&#xff1f;Kubernetes 和 Docker 的关系…
阅读更多...
iOS 17.5中的一个漏洞

iOS 17.5中的一个漏洞

i0S 17.5中的一个漏洞 iOS 17.5中的一个漏洞会使已刚除的照片重新出现&#xff0c;并目此问题似乎会影响甚至已擦除并出售给他人的 iPhone 和 iPad. 在2023年9月&#xff0c;一位Reddit用户根据Apple的指南擦除了他的iPad&#xff0c;并将其卖给了一位朋友。然而&#xff0c;这…
阅读更多...
Spring @Transactional 事务注解

Spring @Transactional 事务注解

一、spring 事务注解 1、实现层(方法上加) import org.springframework.transaction.annotation.Transactional;Transactional(rollbackFor Exception.class)public JsonResult getRtransactional() {// 手动标记事务回滚TransactionAspectSupport.currentTransactionStatus…
阅读更多...
Python第二语言（二、Python语言基础）

Python第二语言（二、Python语言基础）

目录 1. python中常用的6中数据类型 2. Print语句&#xff08;输出程序&#xff09; 3. 字面量 4. 注释 5. 变量 6. 数据类型 7. type()语句&#xff1a;查询数据类型 8. 数据类型转换语句 9. 标识符 10. 算术运算符 11. 赋值运算符 && 复合赋值运算符 12. …
阅读更多...
Polar Web【困难】上传

Polar Web【困难】上传

Polar Web【困难】上传 Contents Polar Web【困难】上传探索&思路&效果进入环境绕过过程Webshell连接 EXPPayload 总结 探索&思路&效果 本题的主题可见为文件上传&#xff0c;详情在破解的过程中逐步发掘&#xff1a; 进入环境&#xff0c;为一个文件上传功界面…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023