文章目录
- 决策树算法
- 1、决策树树状图
- 2、选择最优决策条件
- 3、决策树算法过程
- →白话决策树原理
- 决策树构建的基本步骤
- 常见的决策树算法
- 决策树的优缺点
【五分钟机器学习】可视化的决策过程:决策树 Decision Tree
关键词记忆:
纯度、选择最优特征分裂、熵、基尼不准度、均方误差
决策树算法
1、决策树树状图

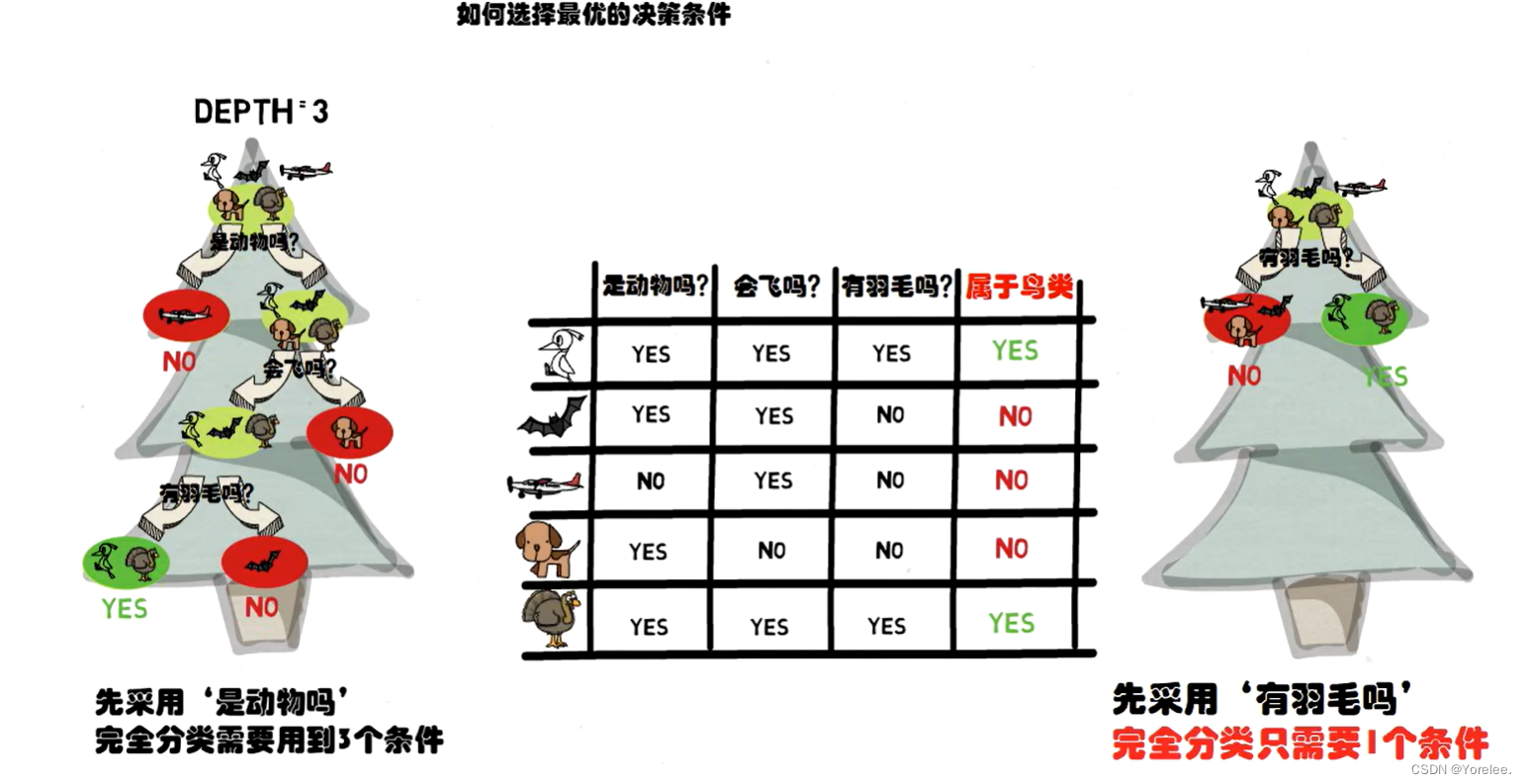
2、选择最优决策条件
3、决策树算法过程
决策树是一种常用于分类和回归的监督学习算法。它模拟了人类决策过程的思维方式,通过构建一个树形结构,其中每个内部节点代表一个属性上的判断,每个分支代表该判断的结果,而每个叶节点代表一个预测结果。下面是关于决策树的详细解释,包括其构建过程和常见算法。
→白话决策树原理
- 分类问题
- 在分类问题上,首先整个数据集是根结点,然后选择最优特征进行分割数据集,即对数据集进行分类,这个选择的最优特征一般是使得分割后的不同子集纯度更高的特征子集,然后依次对每一个分裂后的节点递归分裂,直到每个叶节点达到一个标准,或者深度达到限制条件。
- 根据说的,选择最优决策条件,我们可以知道,根据不同指标进行数据集划分,得到的树深度和性能是不一样的。决策树通过某种标准(如信息增益、信息增益比、基尼不纯度等)来评估每个特征的分割效果。这个标准通常旨在选择能最大化子集纯度的特征。
- 信息增益:选择使得结果集熵减最大的特征。
- 基尼不纯度:选择最小化分割后各节点基尼不纯度的特征。
随机森林分类时使用
- 根据说的,选择最优决策条件,我们可以知道,根据不同指标进行数据集划分,得到的树深度和性能是不一样的。决策树通过某种标准(如信息增益、信息增益比、基尼不纯度等)来评估每个特征的分割效果。这个标准通常旨在选择能最大化子集纯度的特征。
- 在实际应用中,决策树的构建不仅是为了提高模型在训练数据上的性能,更重要的是要保证模型对未知数据的泛化能力。因此,常常需要通过剪枝技术来减少模型的过拟合风险。剪枝可以在树完全生成后进行(后剪枝),也可以在构建过程中进行(预剪枝)。
- 回归问题
- 分类问题和回归问题不一样的是,选择最优决策条件上的指标不一样,回归问题一般采用均方误差或者平均绝对误差。在回归树中,选择特征和分割点的标准通常是最小化每个子节点内的数据方差(或标准误差的减少)
决策树构建的基本步骤
- 选择最佳分割特征:
决策树通过选择最佳的特征来分割数据集。选择标准通常基于信息增益、信息增益比、基尼不纯度或均方误差等统计方法。
- 普通决策树会在每个分裂点所有特征中选择出最佳特征来分割数据集
- 随机森林是先随机选择特征的子集,然后再这个子集中进行最佳特征选择。即在决策树的分裂时特征空间的选择具有随机性。
-
分割数据集:
一旦选择了一个特征,数据集会根据该特征的不同取值被分割成不同的子集。这个过程会递归地在每个子集上重复进行,直到满足停止条件。 -
递归构建树:
对每个子集应用相同的方法,递归地构建决策树的每个分支,直到达到某个停止条件,例如设置的最大深度、节点中的最小样本数或节点的纯度(比如,所有样本都属于同一类别)。 -
剪枝:
树构建完成后,为防止过拟合,通常需要对树进行剪枝。剪枝可以通过预剪枝(在构建过程中提前停止树的增长)或后剪枝(删除树的某些部分)来实现。
常见的决策树算法
-
ID3(Iterative Dichotomiser 3):
- 使用信息增益作为标准来选择分割的特征。
- 仅能用于分类任务,并且只处理离散特征。
-
C4.5:
- 后续版本的ID3,使用信息增益比来选择特征。
- 能处理连续和离散特征,同时引入了树的剪枝过程。
-
CART(Classification and Regression Trees):
- 用于分类和回归的决策树算法。
- 对于分类问题使用基尼不纯度作为标准,对于回归问题使用均方误差。
- 总是产生二叉树。
随机森林采用的方法
决策树的优缺点
优点:
- 易于理解和解释,决策树可以可视化。
- 能够同时处理数值型和类别型数据。
- 对中间值的缺失不敏感。
缺点:
- 易于过拟合,尤其是树较深或样本较少时。
- 对于那些各类别样本量差异较大的数据集,信息增益的偏见问题。
- 不稳定性,小的数据变化可能导致树的显著变化。
决策树是机器学习中非常基础且强大的模型,常作为许多先进算法(如随机森林、梯度提升树)的基石。理解其基本原理和操作是掌握更复杂模型的关键。
随机森林通常使用的决策树模型是 CART(Classification and Regression Trees)树。CART 是一种广泛使用的决策树学习技术,它可以用于分类和回归任务。CART 树使用基尼不纯度(Gini impurity)作为在单棵树中用于指导如何进行节点分裂从而构建决策树的默认标准,;均方误差(Mean Squared Error, MSE)或平均绝对误差(Mean Absolute Error, MAE)来处理回归问题。