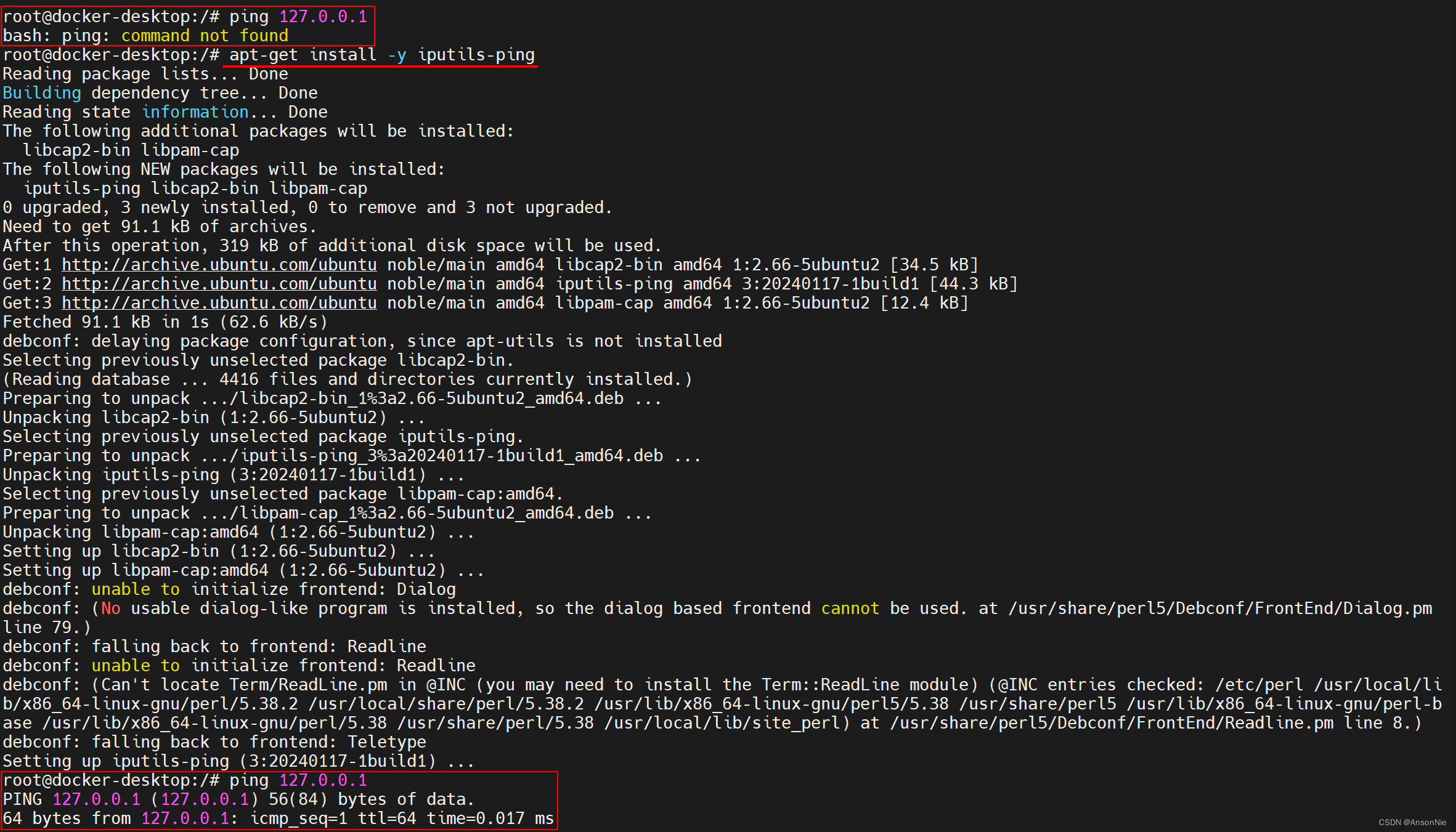
第N次被作者打倒了,第5章46题解题上集的记录

计算均值的代码段
step_num = 0
num_c = 0
pow_c = 0
while step_num < 10:
a = eval(input("Enter number is: "))
num_c += a
pow_c += pow(a, 2)
step_num += 1
t2 = num_c / 10
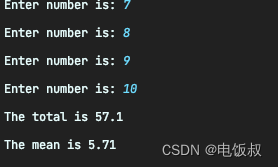
这个结果和书里的答案差一点。书里写的是1,2,3,5.5,5.6,6,7,8,9,10,这些数统计起来的均值是5.61 , 我变成了5.71 不知道是不是差在哪里??
好了接下来是最头疼的地方,标准方差,根据书里 给的公式。我得出了无数可怕的结果。根本对不上。这个也可能是我理解错误。我感觉我的数学要好好从头学。

这个公式我的理解
(1+2+3+5.5+5.6+6+7+8+9+10)/10
我似乎理解对了

到了这里呢!!!
我现在理解是1平方+2平方+3平方+5.5平方+5.6平方+6平方+7平方+8平方+9平方+10平方=405.61
然后减(1+2+3+5.5+5.6+6+7+8+9+10)的平方再除(n-1)
可是按照这个逻辑 我得到所谓的-2ee132131415151
代码如下
while step_num < 10:
a = eval(input("Enter number is: "))
num_c += a
pow_c += pow(a, 2)
step_num += 1
t2 = num_c / 10
c = (pow_c - (pow(num_c, 2))) / (step_num - 1) ** 0.5

此结果和wps以及excel结算的一样。

这个是用wps算的
现在的问题是我按作者给的公式根本不成功.
利用wps计算


wps和python的计算结果一个是NUM!一个是-951.6
作者的文章真的,不是我这个数学为0的人能看的懂。经过半个月的寻找。我发现了一个公式可以接近作者的结果


现在经过wps的再次计算