前言
树状数组或二叉索引树(Binary Indexed Tree),又以其发明者命名为 Fenwick 树。其初衷是解决数据压缩里的累积频率的计算问题,现多用于高效计算数列的前缀和、区间和。它可以以 O(logn) 的时间得到任意前缀和。并同时支持在 O(logn) 时间内支持动态单点值的修改。空间复杂度 O(n)。
介绍
1.原理
树状数组,顾名思义是树状的数组,我们首先引入二叉树,叶子节点代表A[1]~A[8]。
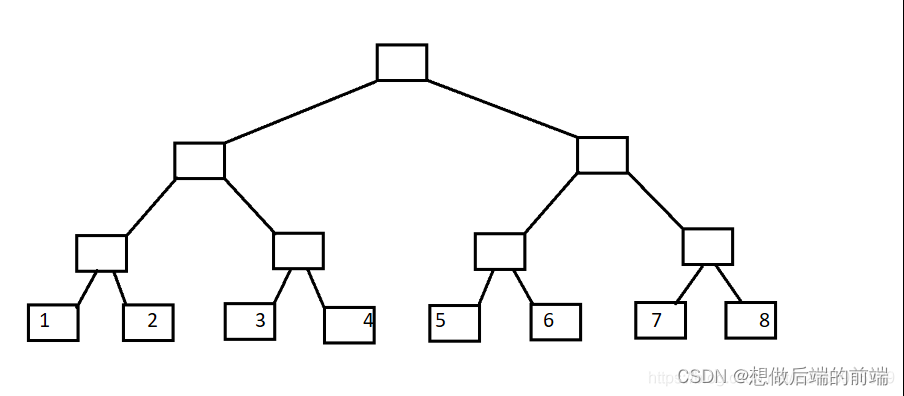
现在变形一下:
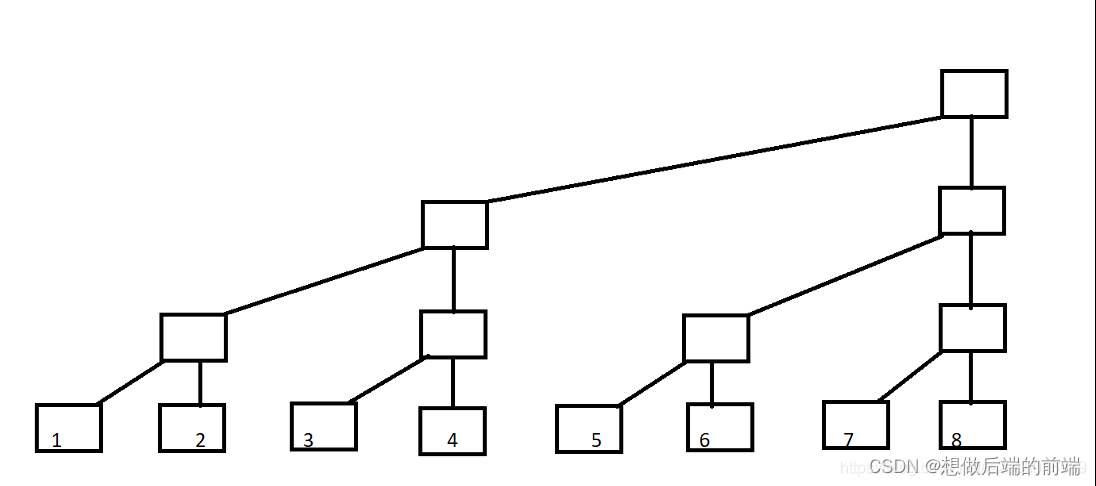
现在定义每一列的顶端节点C数组(其实C数组就是树状数组),如图:

理解树状数组的重点
C[i]代表子树的叶子节点的权值之和,如图可以知道:
C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
看过上面的列表,有没有看出来什么规律来呢?
如果没有看出来,那说明你不知道lowbit函数。
先看lowbit函数的代码:
function lowBit(x){
return x&-x;
}
不知道干啥的吧!是不是一脸懵逼?别慌,举几个例子:
1 & -1 = 1;
2 & -2 = 2;
3 & -3 = 1;
4 & -4 = 4;
5 & -5 = 1;
6 & -6 = 2;
7 & -7 = 1;
8 & -8 = 8;
对比上面的,熟悉不,看出来规律了吗?
怎么理解呢?
lowbit函数的含义即为:x(二进制)最低位1后面的0组成的数
例如:
5(二进制:101)最低位1后面0的个数为0,则lowbit(5)=2^0=1(十进制)
12(二进制:1100) 最低位1后面0的个数为2,则lowbit(12)=2^2=4(十进制)
那现在我给你一个数组,让你求解他的树状数组,能求出来吗?思考一下解出来了就跳过下面。或者对一下答案!
var A = [1,2,3,4,5,6,7,8]
var C = new Array(9).fill(0);
function getSum(i) {
let begin = lowBit(i);
let res=0;
while(begin) {
res += A[i-begin];
begin --;
}
return res;
}
for(let i=1;i<9;i++){
C[i] = getSum(i);
}
console.log("树状数组",treeArr);
//[0,1, 3, 3, 10, 5, 11, 7, 36]
//注意哦我不要第一项,至于为什么,懂得都懂。
2.应用
2.1 区间查询
利用C[i]数组,求A数组中前i项和,举两个栗子:
前7项和:
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7];
而C[4]=A[1]+A[2]+A[3]+A[4];C[6]=A[5]+A[6];C[7]=A[7];
可以得到:sum[7]=C[4]+C[6]+C[7]。
数组下标写成二进制:sum[(111)]=C[(100)]+C[(110)]+C[(111)];
前5项和:
sum[5]=A[1]+A[2]+A[3]+A[4]+A[5];
而C[4]=A[1]+A[2]+A[3]+A[4];C[5]=A[5];
可以得到:sum[5]=C[4]+C[5];
数组下标写成二进制:sum[(101)]=C[(100)]+C[(101)];
细细观察二进制,树状数组追其根本就是二进制的应用,结合代码演示一下代码过程:
function finSum(i){
let res = 0;
while(i){
res += treeArr[i];
i -= lowBit(i)
}
return res;
}
console.log("前5项和",finSum(5)); //15
console.log("前7项和",finSum(7)); //28
代码推演:
lowbit(5)=001 5-lowbit(5)=4(100) ans+=C[4]
lowbit(4)=100 4-lowbit(4)=0(000) break;
看到这里是不是有点疑惑,这不比前缀算法还多算了一个树状数组吗?我也有这个疑问,保留意见,先继续往下看。
2.2 单点更新
当我们修改A数组中某个值时,应当如何更新C数组呢?回想一下,区间查询的过程,再看一下上文中列出的过程。这里声明一下:单点更新实际上是不修改A数组的,而是修改树状数组C,向上更新区间长度为lowbit(i)所代表的节点的值。
function update(i,k){
A[i] += k;
while(i <= 8){
C[i] += k;
i += lowBit(i);
}
}
update(6,5);
console.log("前5项和",finSum(5)); //15
console.log("前7项和",finSum(7)); //33

如上图:若在A[1]加上值val,即更新A[1]时,需要向上更新C[1],C[2],C[4],C[8],这个时候只需将这4个节点每个节点的值加上val即可。这里为了方便大家理解,人为添加了个A数组表示每个叶子节点的值,事实上A数组并不用修改,实际运用中也可不设置A数组,单点更新只需修改树状数组C即可。下标写成二进制:C[(001)],C[(010)],C[(100)],C[(1000)];
lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=val;
lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=val;
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=val;
由于c[1] c[2] c[4] c[8] 都包含有A[1],所以在更新A[1]时实际上就是更新每一个包含A[1]的节点。
现在是不是有点懵懂了,如果用前缀和的话,需要在1后面的所有元素都加上val,但是对于树状数组就不同了。时间复杂度为O(logN)
与线段树对比
1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.
2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.
3. 树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作,其代码效率远高于线段树。