心得
赛中ac:5,目前ac:9,题目总数:13
中档可做题还是很多的,可惜遇到了难绷的queueforces,
最后15min才判出来,oi赛制5wa4遗憾离场,赛后把几个题都给调过了,写下题解
题目
J. Breakfast(签到)
签到,不过不是很懂python直接输出39.20为啥wa了
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
int n,m;
int main(){
sci(n),sci(m);
printf("%.2lf\n",0.6*n+m);
return 0;
}A. Paper Watering(枚举)
先特判1,
对于非1的情况,首先原数是可以一直平方不重的,
如果x开根号遇到了下取整,说明sqrt(x)*sqrt(x)也不会和x重,后续平方也都不会重
暴力模拟这个过程,直至出现1为止
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
int x,k;
ll ans;
int main(){
sci(x),sci(k);
if(x==1){
puts("1");
return 0;
}
ans=k+1;
rep(i,1,k){
int v=sqrt(x);
if(v==x)break;
if(1ll*v*v==x){
ans++;
}
else{
if(v==1)ans++;
else ans+=1+k-i;
}
x=v;
}
ptlle(ans);
return 0;
}D. nIM gAME(博弈)
发现后手可以控制倒数第二张牌取什么,从而使先手必败
//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
int t,n;
int main(){
sci(t);
while(t--){
sci(n);
puts("lose");
}
return 0;
}E. Checksum(枚举)
枚举最终的d有几个1,从而唯一确定后缀补的1的数量和位置,输出即可
//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=2e5+10;
int t,n,k;
char s[N];
int main(){
sci(t);
while(t--){
sci(n);sci(k);
scanf("%s",s+1);
int c=0;
rep(i,1,n)c+=(s[i]=='1');
int ans=1e9;
rep(j,c,c+k){
int v=j&((1<<k)-1);
if(__builtin_popcount(v)==j-c){
ans=min(ans,v);
}
}
if(ans==1e9)puts("None");
else{
per(j,k-1,0){
printf("%1d",ans>>j&1);
}
puts("");
}
}
return 0;
}L. Bracket Generation(计数)
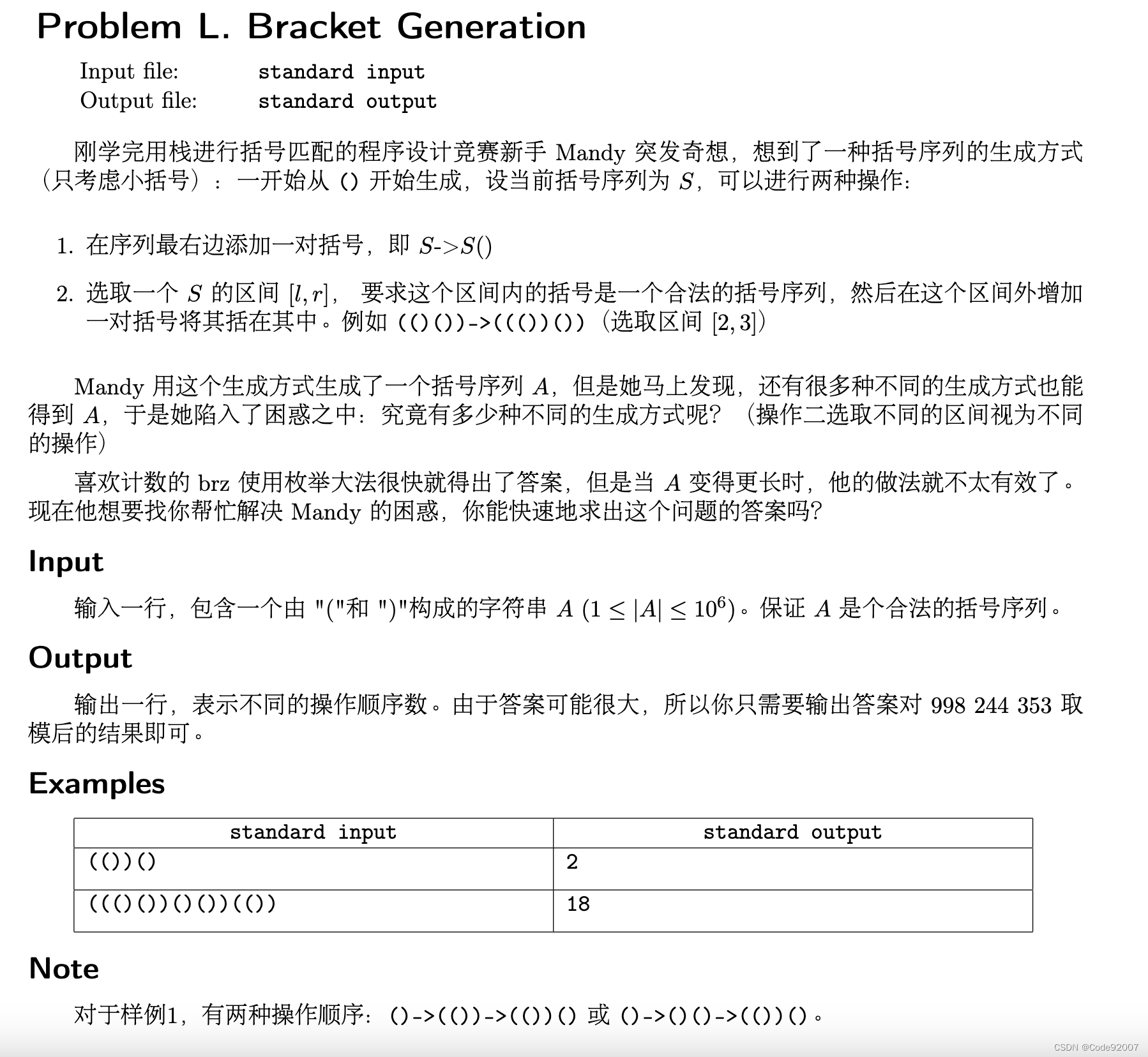
一开始把第二个条件看错了,以为只有内层的选完了外层的才能选,没有这个限制之后就很好做
把左右括号相邻的()括号称为叶子节点(建括号树更直观),其他的称为非叶节点
非叶节点能选当且仅当其包含的最大叶子结点x及序列里位于x左侧的叶子结点都选完之后,才能选
将序列倒着考虑,就是非叶节点的一个插空问题
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=2e6+10,M=2*N,mod=998244353;
char s[N];
int n,cnt,lim[N];
int main(){
scanf("%s",s+1);
n=strlen(s+1);
rep(i,1,n){
if(s[i]==')' && s[i-1]=='(')cnt++;
if(s[i]==')' && s[i-1]!='('){
lim[i]=cnt;
}
}
int now=0,ans=1;
per(i,n,1){
if(!lim[i])continue;
ans=1ll*ans*(cnt-lim[i]+now+1)%mod;
now++;
}
pte(ans);
return 0;
}F. Factor(数论)

先把p、k分别质因数分解,求出对应质因数和出现的幂次
对于p的质因子f,如果f也是k的质因子,显然出现多少次都无所谓,都能除尽,删掉这些f
对于p的独有质因子(也就是没有出现在k中的质因子)p1、p2、…,
记每个的最高幂次是k1、k2、…,将这些最高幂次乘起来得到y,
枚举y的因子z,也就是这些独有质因子出现了多少,
分母必须恰好能和z兑掉,且剩下的部分由k出现过的质因子构成,
在[1,x/z]内仅由k出现过的质因子构成的数,这个可以先预处理出所有,再二分
因为仅由质因子组成,所以数量没有太多
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int maxp = 1e7+10;
int t, tot, pr[maxp], d[maxp];
ll p,x,k,now,ans;
vector<P>f,f2;
vector<ll>g,all;
map<ll,bool>mp;
void dfs(ll v,int y){
all.pb(v);
int sz=SZ(g);
for(int i=y;i<sz;++i){
if(1ll*v<=x/g[i])dfs(v*g[i],i);
}
}
void sol(ll v,int y,int z){
ans+=upper_bound(all.begin(),all.end(),x/v)-all.begin();
int sz=SZ(f2);
if(y==sz)return;
//printf("v:%lld y:%d z:%d fi:%lld se:%d\n",v,y,z,f2[y].fi,f2[y].se);
if(1ll*v<=x/f2[y].fi && z+1<=f2[y].se)sol(v*f2[y].fi,y,z+1);
for(int i=y+1;i<sz;++i){
if(1ll*v<=x/f2[i].fi)sol(v*f2[i].fi,i,1);
}
}
int main(){
for(int i = 2; i < maxp; ++i) {
if(!d[i])
pr[tot++] = d[i] = i;
for(int j = 0, z; (z = i * pr[j]) < maxp; ++j) {
d[z] = pr[j];
if(d[i] == pr[j])
break;
}
}
scanf("%lld%lld%lld",&p,&x,&k);
rep(i,0,tot-1){
if(1ll*pr[i]*pr[i]>p){
break;
}
if(p%pr[i]==0){
f.pb(P(pr[i],0));
while(p%pr[i]==0)p/=pr[i],f.back().se++;
}
}
if(p>1)f.pb(P(p,1));
//for(auto &x:f)printf("(p:%lld,c:%lld)\n",x.fi,x.se);
rep(i,0,tot-1){
if(1ll*pr[i]*pr[i]>k){
break;
}
if(k%pr[i]==0){
g.pb(pr[i]);
mp[pr[i]]=true;
while(k%pr[i]==0)k/=pr[i];
}
}
if(k>1){
g.pb(k);
mp[k]=true;
}
//for(auto &x:g)printf("(g:%lld)\n",x);
for(auto &v:f){
if(mp.count(v.fi))continue;
f2.pb(v);
}
//for(auto &v:f2)printf("(%lld,%lld) ",v.fi,v.se);puts("");
dfs(1,0);
sort(all.begin(),all.end());
//for(auto &v:all)printf("(v:%lld)\n",v);
sol(1,0,0);
ptlle(ans);
return 0;
}I. Password(dp)

dp[i]表示[1,i]是合法答案的方案数
转移枚举最后一段的长度x,最后这一段和前面的x-k共同拼成了一个长度为k的排列
但是枚举长度为2的时候,会和长度为1的方案有重复,具体来说
不妨k=5,前5个肯定只能是一个排列,k!种方案,不妨是1 2 3 4 5,对于第6个往后,
对于x=1,1 2 3 4 5 [1],
x=2,1 2 3 4 5 [2 1]和 1 2 3 4 5 [1 2]中只能保留第一个,因为第二个和x=1重复了
x=3,同理,只能保留1 2 3 4 5 [3 1 2]、1 2 3 4 5 [3 2 1]和1 2 3 4 5 [2 3 1]
这个系数是需要递推减掉的,手玩发现:
记长度为x的系数是xs[x],对于长度x来说,若y<x,则需要在总数里减掉xs[y]*fac[x-y],
rep(i,1,k){
xs[i]=fac[i];
per(j,i-1,1){
xs[i]=(xs[i]+mod-1ll*xs[j]*fac[i-j]%mod)%mod;
}
//printf("i:%d xs:%d\n",i,xs[i]);
}
O(k^2)预处理出系数之后,再O(nk)dp即可
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=1e5+10,K=1e3+10,mod=998244353;
int n,k;
int xs[K],Finv[N],fac[N],inv[N],dp[N];
void init(int n){ //n<N
inv[1]=1;
for(int i=2;i<=n;++i)inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
fac[0]=Finv[0]=1;
for(int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%mod,Finv[i]=1ll*Finv[i-1]*inv[i]%mod;
//Finv[n]=modpow(fac[n],mod-2,mod);
//for(int i=n-1;i>=1;--i)Finv[i]=1ll*Finv[i+1]*(i+1)%mod;
}
int main(){
sci(n),sci(k);
if(n<k){
puts("0");
return 0;
}
init(n);
dp[k]=fac[k];
//printf("n:%d k:%d\n",n,k);
rep(i,1,k){
xs[i]=fac[i];
per(j,i-1,1){
xs[i]=(xs[i]+mod-1ll*xs[j]*fac[i-j]%mod)%mod;
}
//printf("i:%d xs:%d\n",i,xs[i]);
}
rep(i,k+1,n){
for(int j=1;j<=k;++j){
dp[i]=(dp[i]+1ll*dp[i-j]*xs[j]%mod)%mod;
}
// printf("i:%d dp:%d\n",i,dp[i]);
//dp[i]=(dp[i-1]*fac[1]+dp[i-2]*(fac[2]-fac[1])+dp[i-3]*(fac[3]-fac[2])+...+dp[i-k]*(fac[k]-fac[k-1]))
//dp[i-1]=(dp[i-2]*fac[1]+dp[i-3]*(fac[2]-fac[1])+dp[i-4]*(fac[3]-fac[2])+...+dp[i-k-1]*(fac[k]-fac[k-1]))
//dp[i]-dp[i-1]=dp[i-1]-dp[i-2]+dp[i-2]+dp[i-3]+...+dp[i-k]-dp[i-k-1];
//dp[i]=(2ll*dp[i-1]%mod-dp[i-k-1]+mod)%mod;
}
pte(dp[n]);
return 0;
}M. House(计算几何)

感觉计算几何的题平时不怎么写所以不太会写,
但实际上出题人应该平时也不怎么写,出的题还是挺基础的
先求出矩形,O(n^2logn)枚举点对,将点对放入(线段中点,线段长度)的map内,
矩形的对角线互相平分,所以共用中点且长度相等的两条对角线能构成一个矩形
两两枚举矩形,对于矩形四条边,任意两条邻边x、y检查一下,
统计房子在x外侧的第五个点的个数,这个需要叉积判断不在矩形内部
此时需要统计向量i->j左侧/右侧有多少点,O(n^3)预处理一下即可
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,ll> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=305,M=N*N;
using i64 = long long;
using T = long long;
int n,c;
ll res;
struct Point {
T x;
T y;
Point(T x = 0, T y = 0) : x(x), y(y) {}
Point &operator+=(const Point &p) {
x += p.x, y += p.y;
return *this;
}
Point &operator-=(const Point &p) {
x -= p.x, y -= p.y;
return *this;
}
Point &operator*=(const T &v) {
x *= v, y *= v;
return *this;
}
friend Point operator-(const Point &p) {
return Point(-p.x, -p.y);
}
friend Point operator+(Point lhs, const Point &rhs) {
return lhs += rhs;
}
friend Point operator-(Point lhs, const Point &rhs) {
return lhs -= rhs;
}
friend Point operator*(Point lhs, const T &rhs) {
return lhs *= rhs;
}
}e[N];
T dot(const Point &a, const Point &b) {
return a.x * b.x + a.y * b.y;
}
T cross(const Point &a, const Point &b) {
return a.x * b.y - a.y * b.x;
}
map<array<ll,3>,vector<P>>mp;
vector<P>ans[M];
int pos[N][N],neg[N][N];
void ck(int a,int b,int c){
//printf("a:%d b:%d c:%d res1:%lld\n",a,b,c,res);
if(cross(e[c]-e[b],e[a]-e[b])<0)res+=pos[b][a];
else res+=neg[b][a];
//printf("a:%d b:%d c:%d res2:%lld\n",a,b,c,res);
}
int main(){
sci(n);
rep(i,1,n){
scanf("%lld%lld",&e[i].x,&e[i].y);
}
rep(i,1,n){
rep(j,1,n){
if(i==j)continue;
Point c=e[i]-e[j];
ll z=dot(c,c);
//printf("i:%d j:%d x:%lld y:%lld z:%lld\n",i,j,e[i].x+e[j].x,e[i].y+e[j].y,z);
if(i<j)mp[{e[i].x+e[j].x,e[i].y+e[j].y,z}].pb(P(i,j));
rep(k,1,n){
if(i==k||j==k)continue;
Point ki=e[k]-e[i],kj=e[k]-e[j];
ll x=dot(ki,ki),y=dot(kj,kj);
if(x==y){
ll w=cross(e[k]-e[i],e[j]-e[i]);
if(w>0){
//printf("i:%d j:%d neg:%d\n",i,j,neg[i][j]);
pos[i][j]++;//i->j的逆时针方向 样例房子形状
}else if(w<0){
neg[i][j]++;
//printf("i:%d j:%d neg:%d\n",i,j,pos[i][j]);
}
}
}
}
}
for(auto &x:mp){
ans[++c]=x.se;
}
// rep(i,1,n){
// rep(j,1,n){
// if(i==j)continue;
// printf("i:%d j:%d neg:%d pos:%d\n",i,j,neg[i][j],pos[i][j]);
// }
// }
rep(i,1,c){
int sz=SZ(ans[i]);
rep(j,0,sz-1){
rep(k,j+1,sz-1){
int a=ans[i][j].fi,d=ans[i][j].se,b=ans[i][k].fi,c=ans[i][k].se;
//printf("a:%d b:%d c:%d d:%d res:%lld\n",a,b,c,d,res);
ck(b,a,c);ck(a,c,d);ck(c,d,b);ck(d,b,a);
//printf("a:%d b:%d c:%d d:%d res2:%lld\n",a,b,c,d,res);
}
}
}
ptlle(res);
return 0;
}
/*
5
4 2
0 2
2 5
4 0
0 0
*/G. Diamond(分块)

想到分块之后就很好做了,虽然空间稍微用short卡了一下
先把n弥补成块的倍数,方便后面判断,后面的都用0补足即可,
对于第i个块,预处理出块内任意两种数(x,y)的逆序对个数,
计在这个块内x、y出现的第一个位置big[i][x][y]
所以,也需要记录每种数x在第i个块内出现的第一个位置pos[x][i]是多少,
这个位置可以对块长取模,就是一个最大为块长M(300多)的数,short足矣
然后就是在线查询,
对于长度不超过3*M的块,懒得分类讨论有一个块还是两个了,直接暴力,常数略大一点而已
超过3*M的,一定中间有完整块,然后最多两个半块,
对于每个完整块,先加上完整块的答案;对于半块,暴力统计答案
再从前往后、从后往前遍历块,分别统计块间能产生的答案,求和即可
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<unordered_map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=1e5+1e4+10,M=340;
short pos[N][M];
int big[M][M][M];
int n,T,a[N],l,r,p,q,sq,sz[M][M];
int main(){
sci(n),sci(T);
sq=sqrt(n);
//printf("sq:%d\n",sq);
memset(pos,-1,sizeof pos);
rep(i,0,n-1){
sci(a[i]);
int x=i/sq;
if(pos[a[i]][x]==-1){
pos[a[i]][x]=i%sq;
//printf("i:%d ai:%d x:%d pos:%d\n",i,a[i],x,pos[a[i]][x]);
}
}
while(n%sq)n++;
rep(i,0,(n-1)/sq){
int l=i*sq,r=(i+1)*sq-1;
//printf("i:%d l:%d r:%d\n",i,l,r);
rep(j,l,r){
sz[i][pos[a[j]][i]]++;
rep(k,j+1,r){
if(a[k] && a[j]>a[k]){
int p1=pos[a[j]][i],p2=pos[a[k]][i];
big[i][p1][p2]++;
//printf("i:%d aj:%d ak:%d p1:%d p2:%d big:%d\n",i,a[j],a[k],p1,p2,big[i][p1][p2]);
}
}
}
}
while(T--){
sci(l),sci(r),sci(p),sci(q);
l--;r--;
if(p<q)swap(p,q);
ll ans=0,cp=0,cq=0;
if(r-l+1<=3*sq){
rep(i,l,r){
if(a[i]==p)cp++;
else if(a[i]==q)ans+=cp;
}
ptlle(ans);
continue;
}
int x=l/sq*sq+sq-1,y=r/sq*sq;
rep(i,l,x){
if(a[i]==p)cp++;
else if(a[i]==q)ans+=cp;
}
per(i,r,y){
if(a[i]==q)cq++;
else if(a[i]==p)ans+=cq;
}
rep(i,(x+1)/sq,(y-1)/sq){
int p1=pos[p][i],p2=pos[q][i],v1=0,v2=0;
if(~p1)v1=sz[i][p1];
if(~p2)v2=sz[i][p2];
if(~p1 && ~p2)ans+=big[i][p1][p2];
ans+=1ll*cp*v2;
cp+=v1;
}
ans+=1ll*cp*cq;
ptlle(ans);
}
return 0;
}