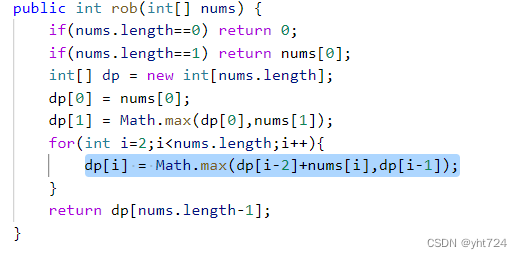
LC198打家劫舍

1. 偷前一家或者偷前两家和这家：dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1]);
2. 代码
   

LC213打家劫舍II（ 未掌握）

1. 解题思路：因为成环了，所以首位元素一定是两者只能选择一个或者两者都不选
2. 三种情况：
   • 首尾元素都不选择，即数组范围为[1,nums.length-2]
   • 选择首元素不选择尾元素，即数组范围为[0,nums.length-2]
   • 选择尾元素不选择首元素，即数组范围为[1,nums.length-1]
3. 以上三种情况都可以看成是单独的打家劫舍问题，因此可知情况二三是包括情况一的
4. 代码
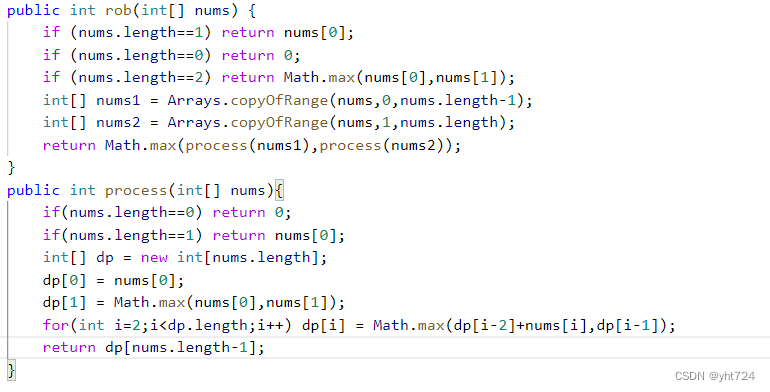
   • 需要注意的是Arrays.copyOfRange(int[] origin,int start,int end)中的end参数是实际end的下一个位置
     

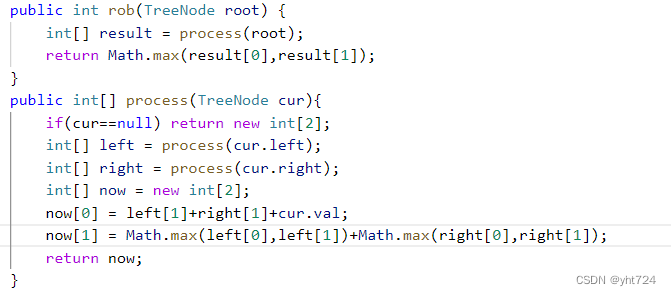
LC337打家劫舍III(未掌握)

1. 未掌握原因分析：如果一个节点没有被偷，那么其子节点可以选择偷或者不偷，不一定就是要偷的
2. 数组0元素表示偷该节点的最大值，1元素表示不偷该节点的最大值
3. 偷：左不偷+右不偷+节点值
4. 不偷：Math.max(左偷，左不偷)+Math.max(右偷，右不偷)
5. 代码