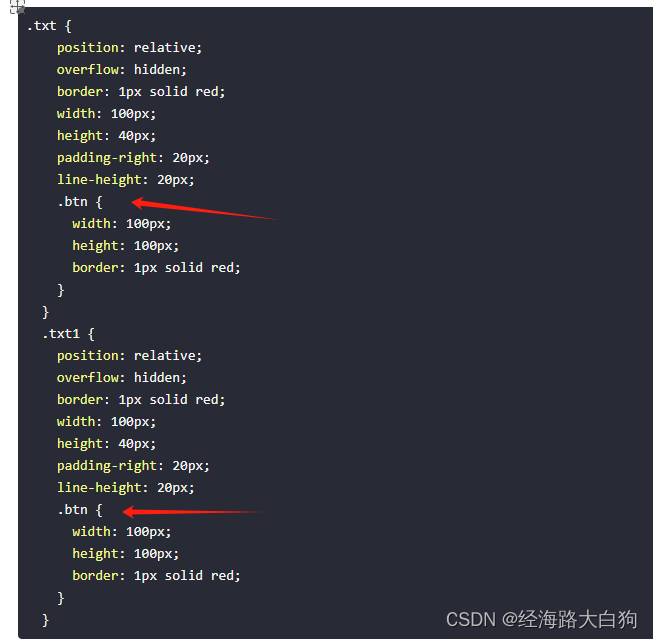
文章目录
- 一、说明
- 二、 inversion和 reflection
- 三、圆反演的定义
- 四、广义的圆反演成圆
关键词:inversion、reflection
一、说明
这里是庞加莱几何的第二篇文章,是庞加莱基本几何属性的研究。本篇主要说清楚,什么是反演,在反演情况下,圆和直线的变换结果。也预先告诉大家,在艺术作图中,反射比反演更常见。除此,还涉及几个定理的证明。
二、 inversion和 reflection
双曲几何可以通过庞加莱圆盘模型或庞加莱半平面模型来建模。在这两个模型中,圆反演都用作测地线中的反射。
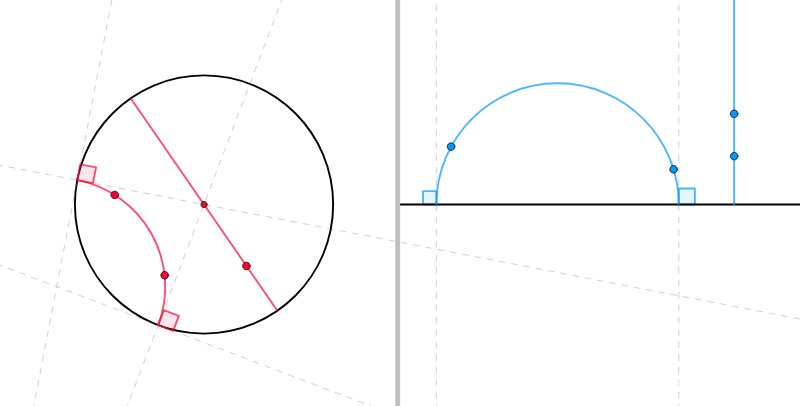
注意,圆的反演和测地线反射的关系:
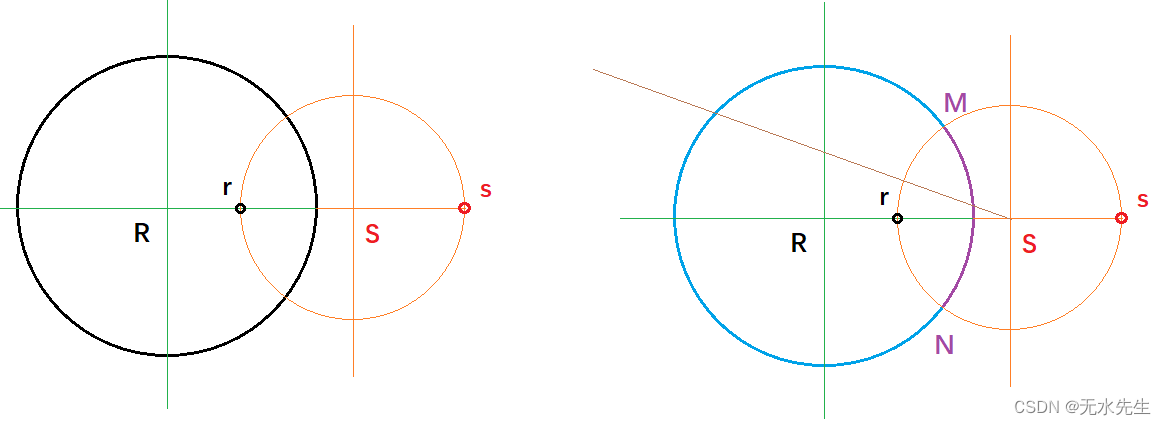
设圆R内有一点r;那么,r的反演点是s;在圆R内,过r的测地线就是S圆的一段弧。因此
1)圆S和R互相构成反演;
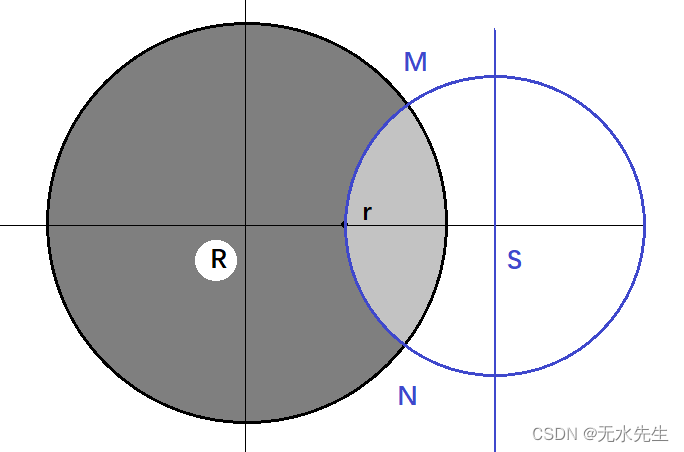
2)S圆分R圆成两部分区域(下图阴影部分),这两部分区域既是R内点关于测地线MN的反射(reflect);同时,这两部分也是S圆关于两部分区域点的反演(inversion)。
3)两个圆(R和S)是垂直关系;
4)两个圆(R和S)是相互反演的关系;
在欧几里得几何中,直线反射的三角形与原始三角形全等。当沿直线反射时,距离和角度都会被保留。
使用庞加莱圆盘模型或庞加莱半平面模型,当物体反射在测地线中时,距离和角度将被保留。这是通过使用反射的圆反转来实现的。双曲角与欧几里得角相同(通过使用测地线的切线测量)。双曲距离的定义方式是在测地线中反射时保留该距离。两点之间的双曲距离与欧氏距离不同。
通过使用圆的反演作为直线欧几里得反射的双曲版本,我们将能够构造双曲工具,例如中点、垂直线和垂直平分线。我们将从定义圆反演开始,然后展示构建双曲线工具所需的圆反演的所有属性。
三、圆反演的定义
如果反转圆c有半径r和中心O,然后A的反演点是A′,那么A′点是一个躺在OA射线上的点。

当A靠近O点时, A′将靠近无穷远,在圆上的点,反演到自己本身。圆内的点必反演到圆外,而圆外的点,必反演到圆内。
可以使用尺子和圆规构建反演点。在 GeoGebra 中,您可以使用工具 Reflect Object in Circle 来创建反演点。
为了显示所需的圆反转的性质,我们需要找到点和反转点之间的关系。
【 定理1】让O 是反转圆 c 的中心。让A 和B 是圆内不等于 O 的不同点, 和这样的A,B, 和 O 不共线。设A′ 和 B′ 是反演点。则△OAB∼△OB′A′。

证明:忽略。
四、广义的圆反演成圆
当一个圆居于单位圆内部时,它就的反演要么为圆、要么是直线。当直线在圆中反转时也是如此,它要么反转为圆,要么反转为直线。
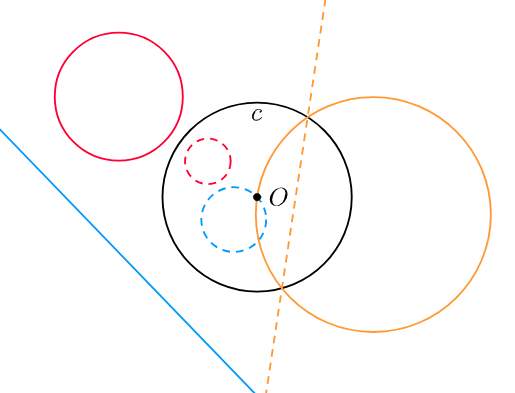
如图:
1)当s圆在单位圆c内部,且s不过c的圆心,那么。s的反演在c的外部的圆。
2)当t圆在单位圆c内部,且t不过c的圆心,那么。t的反演在c的外部的直线。
3)当w圆在单位圆c内外部,且w过c的圆心,那么。w的反演在c的内外部的直线。
4)如果直线经过O点,那么它反演到自身的直线。
为了方便起见,不区分圆和线,而是使用所谓的广义圆,即要么是圆要么是线的几何对象。使用 GeoGebra,您可以在圆和直线上使用“在圆中反射对象”工具。
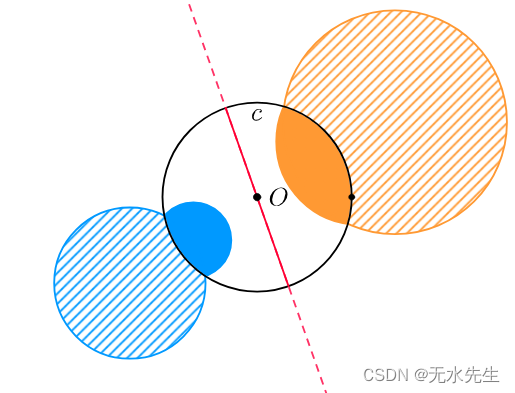
圆和直线的圆反转的不同情况如下:
【定理2】:圆和线的圆反转的不同情况如下
- 让O 是反转圆 c 的中心。过 O 的线 与自身反转。不经过 O 的直线 通过 O 倒转为圆。
- 相反,通过 O 的圆 反转为一条不经过 O 的线。
- 不经过 O 的圆 ,倒转为不通过 O圆。
证明:
我们必须证明这三种情况中每一种情况的定理。
- 1 【情况1】 ‐ 一个贯穿O的线上点,反演到线本身。
让
l
l
l是一条线
O
O
O并让一个和
B
B
B两点上
l
l
l.倒线由倒置点定义
A
′
A^′
A′和
B
′
B^′
B′.倒置的点在来自的光线上O自一个和B分别。由于两条射线都亮着l倒置点必须都打开
l
l
l.因此,反转线与
l
l
l线共线.
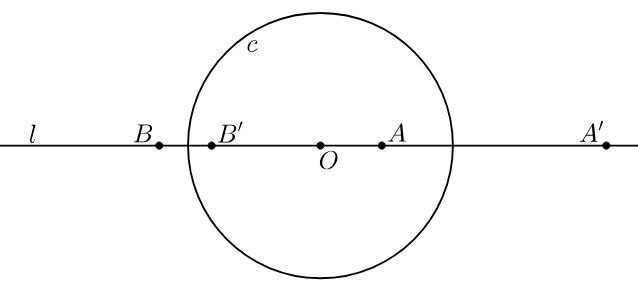
- 2 【情况 2】 ‐ 设O是反演圆,一条线不通过O,通过反演成一个过O的圆.相反,一个圆圈通过O被反转为一条不通过O的线.
让 l l l是一条不通过 O O O的线.再划一条线 O O O垂直于 l l l并让一个是两条线之间的交点。让 B B B是另一点 l l l.
- 表明 ∠ O B ′ A ′ ∠OB^′A^′ ∠OB′A′是直角。
- 使用 1) 的结论和练习 2 的结论来证明一条线不通过O通过倒置成一个圆O.
通过逆转这个过程,我们可以证明循环通过O(不包括点O) 反转为不通的线O.您不必这样做。
- 3【案例 3】 ‐ 圆圈不通过O反演成一个圆圈,而不是通过O.
证明定理2的情况3:
将 O 视为反转圆的中心。不穿过 O 的圆反转为另一个也不穿过 O 的圆。用完全位于反转圆内的圆来证明这一点。
取 d 作为反演圆内不经过 O 的圆。设 A 为 d 上距离 O 最近的点,B 为 d 上距离 O 最远的点。设 C 为 d 上与 A 不同的任何其他点, B. 将点 A、B 和 C 的反转分别表示为 A’、B’ 和 C’。
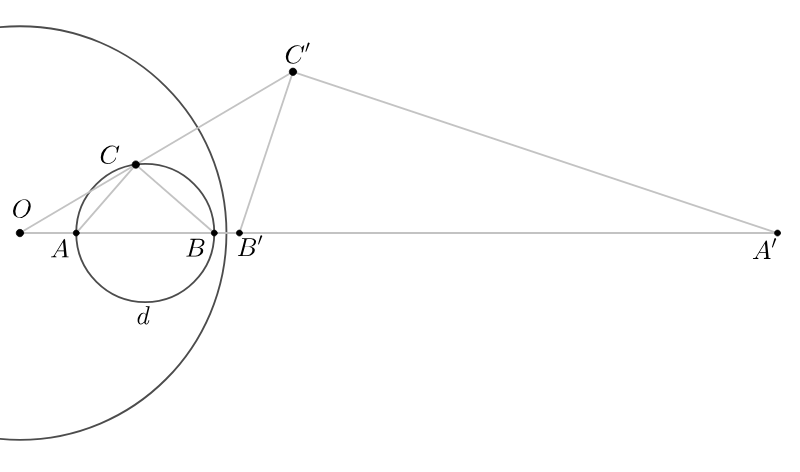
由于C的任意性,且∠ACB始终是直角,∠A‘C’B‘也始终是直角,因此,圆d被映射到圆⚪A‘C’B‘上。










![[word] word如何清除超链接 #媒体#笔记#知识分享](https://img-blog.csdnimg.cn/img_convert/eec2e03c62507d5043f72728f015a515.gif)
