【数据结构】极致详解：树与二叉树（中）——顺序存储实现

news2025/1/12 21:41:18

目录

📔前言📔：

📙一、顺序存储结构📙：

📘二、堆📘：

1.堆的概念及结构：

2.堆的性质：

3.堆的实现（本文重点）：

①.堆的初始化：

②.堆的插入（含向上调整算法）：

③.堆的删除（含向下调整算法）：

④.取堆顶数据：

⑤.堆中数据个数：

⑥.堆的判空：

⑦.堆的销毁：

4.堆实现全部代码：

①.Heap.h：

②.Heap.c：

③.test.c：

📕总结📕：

🛰️博客主页：✈️銮同学的干货分享基地

🛰️欢迎关注：👍点赞🙌收藏✍️留言

🛰️系列专栏：🎈 数据结构

                       🎈【进阶】C语言学习

                       🎈  C语言学习

🛰️代码仓库：🎉数据结构仓库

                       🎉VS2022_C语言仓库

        家人们更新不易，你们的👍点赞👍和⭐关注⭐真的对我真重要，各位路过的友友麻烦多多点赞关注，欢迎你们的私信提问，感谢你们的转发！

        关注我，关注我，关注我，你们将会看到更多的优质内容！！

🏡🏡 本文重点 🏡🏡：

🚅 顺序存储结构 🚃 堆 🚏🚏

📔前言📔：

        上节课中我们完整、宏观的认识了树与二叉树，以及两种常见的存储结构的相关概念与整体结构，而今天我们就将来研究两种存储结构中的一种——顺序存储结构的实现。

📙一、顺序存储结构📙：

        普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆（一种二叉树）使用顺序结构的数组来进行存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆完全不同，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

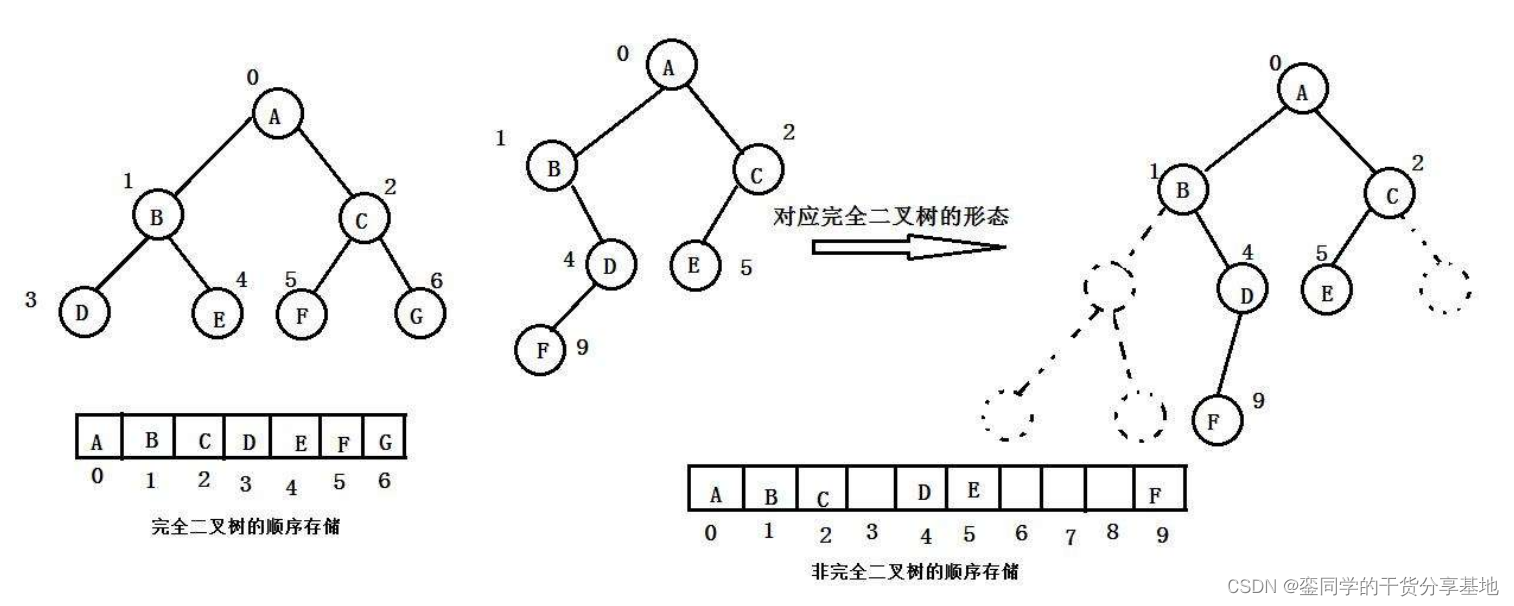
        于是今天我们关于顺序存储结构的研究与讲解，就以堆的形式进行。

📘二、堆📘：

1.堆的概念及结构：

        堆分为小根堆和大根堆，根节点始终小于子节点称为小根堆，相反根节点始终大于子节点则称为大根堆。换句话说，将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

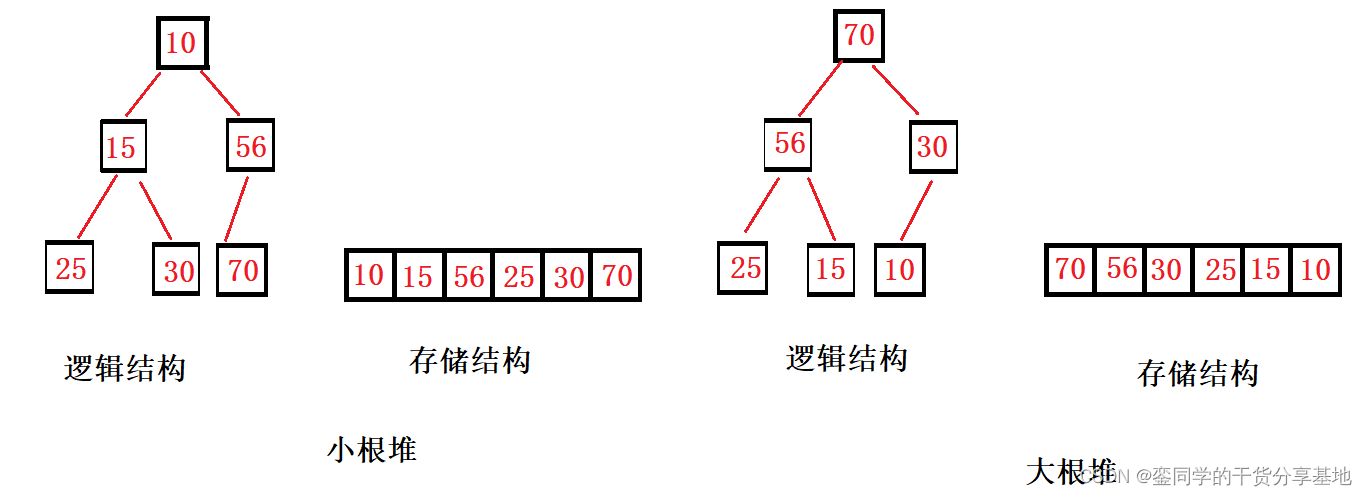
2.堆的性质：

  • 堆中某个节点的值总是不大或不小于其父节点的值。
  • 堆总是一棵完全二叉树。

3.堆的实现（本文重点）：

        关于堆的实现我们使用标准模块化开发格式进行研究：

 
  • Heap.h：存放函数声明、包含其他头文件、定义宏。
  • Heap.c：书写函数定义，书写函数实现。
  • test.c：书写程序整体执行逻辑。

 

①.堆的初始化：

  • 堆的初始化与队列相同，首先判断传入指针非空后，将其置空，并将数据置零即可。 
void HInit(HP* p)
{
	if (p == NULL)
	{
		printf("Init Error!\n");
		return;
	}
	p->a = NULL;
	p->size = p->capacity = 0;
}

②.堆的插入（含向上调整算法）：

        因为堆的存储在物理层面上数组，但是在逻辑层面上二叉树。并且由于只有小根堆和大根堆，所以在插入数据之后要想保证其仍然是堆，就需要进行适当的调整。插入时从尾部插入，而是否为堆取决于子节点和父节点的关系，所以插入的数据要与其父节点进行比较，若为小根堆则子节点要比父节点要大，否则就需要交换子节点和父节点，大根堆则相反。而这种调整方式就叫做向上调整算法。

  • 执行操作前需进行非空判断，防止堆空指针进行操作。 
  • 插入前判断空间是否足以用于此次扩容，若不足则进行扩容，直至满足插入条件后堪称插入操作，这个接口的功能实现也与队列的处理方式基本相同。
  • 与队列的不同点在于，为了保证插入后仍然是堆，需要在插入后使用向上调整算法进行适当的调整。
//向上调整算法：
void AdJustUp(int* a,int n,int child)
{
	if (a == NULL)
	{
		printf("AdJustUp Error!\n");
		return;
	}
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//大根堆节点交换(判断小根堆秩序将">"换为"<"即可)：
		if (a[child] > a[parent])
		{
			HDataTapy tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;
			//重复向上走：
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

//堆插入：
void HPush(HP* p, HDataTapy x)
{
	if (p == NULL)
	{
		printf("Push Error!\n");
		return;
	}
	if (p->size == p->capacity)
	{
		//插入前扩容：
		size_t newCapacity = (p->capacity == 0) ? 4 : (p->capacity * 2);
		HDataTapy* tmp = realloc(p->a, sizeof(HDataTapy) * newCapacity);
		//判断扩容结果：
		if (tmp == NULL)
		{
			printf("Capacuty Get Error!\n");
			return;
		}
		//增容成功后的处理：
		else
		{
			p->a = tmp;
			p->capacity = newCapacity;
		}
	}
	//插入数据：
	p->a[p->size] = x;
	p->size++;
	//向上调整：
	AdJustUp(p->a, p->size, p->size - 1);
}
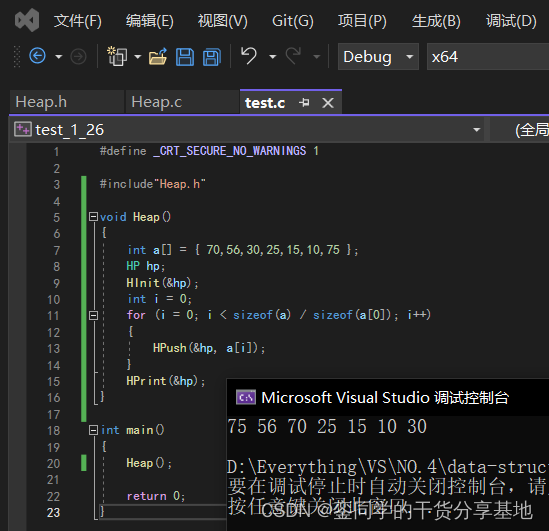
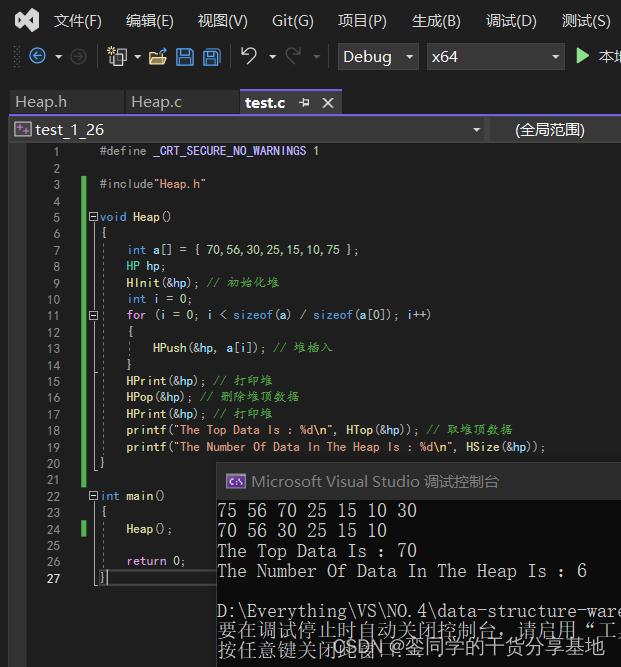
  • 验证堆插入接口功能实现：

 

③.堆的删除（含向下调整算法）：

        堆删除的实质是删除堆顶元素，如果我们直接删除堆顶的元素，再将数据挪动，就会破坏堆的结构，所以这种方法并不可取；于是我们这里采用将堆顶的数据与最后一个数据交换，再删除最后一个数据的方法，这样就实现了堆顶数据的删除。接着我们再调整一下堆顶数据的位置即可。

        在这里，我们选择的调整方法是：将根节点与它的孩子中的较小值交换，然后再将交换后的节点作为父节点继续与它的子节点交换，直到该节点小于它的子节点，或者成为叶节点。要注意的是，使用这个方法有一个前提：根节点的两个子树也得是堆才行。而这种方法就叫做向下调整算法。

  • 执行操作前需进行非空判断，防止对空指针进行操作。 
  • 删除过程同样与队列近乎一致，不同点是在删除过后为了保证删除堆顶数据后仍为堆，于是需要使用向下调整算法堆删除后的结果进行适当的处理。
//向下调整算法：
void AdJustDown(int* a, int n, int parent)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		//选出两孩子中的较小孩子(需要考虑边界，防止越界访问)：
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;
		}
		//向下调整：
		if (a[child] > a[parent])
		{
			int* tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//堆顶数据删除：
void HPop(HP* p)
{
	if (p == NULL)
	{
		printf("Pop Error!\n");
		return;
	}
    //堆数据判空：
	if (HEmpty(&p) == 1)
	{
		printf("Is Null !\n");
		return;
	}
	HDataTapy* tmp = p->a[0];
	p->a[0] = p->a[p->size - 1];
	p->a[p->size - 1] = tmp;
	p->size--;
	AdJustDown(p->a, p->size - 1, 0);
}
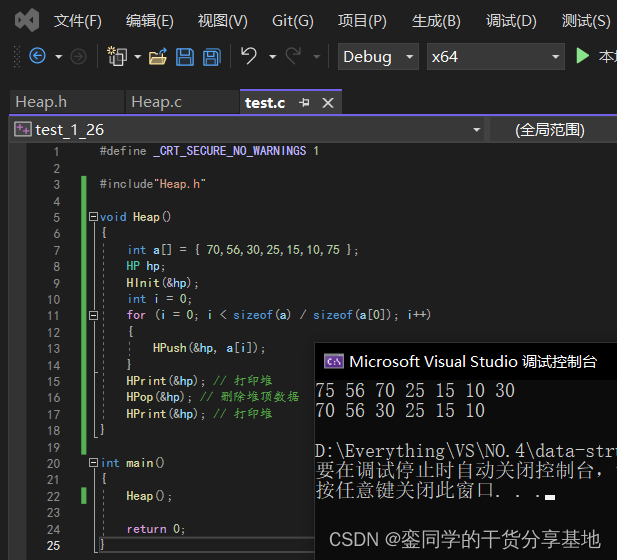
  • 测试删除接口功能实现：

④.取堆顶数据：

  • 取堆顶数据操作与队列完全相同，这里不再作过多阐述。
HDataType HTop(HP* p)
{
	if (p == NULL)
	{
		printf("Top Get Error!\n");
		return;
	}
	//堆数据判空：
	if (HEmpty(&p) == 1)
	{
		printf("Is Null !\n");
		exit;
	}
	return p->a[0];
}
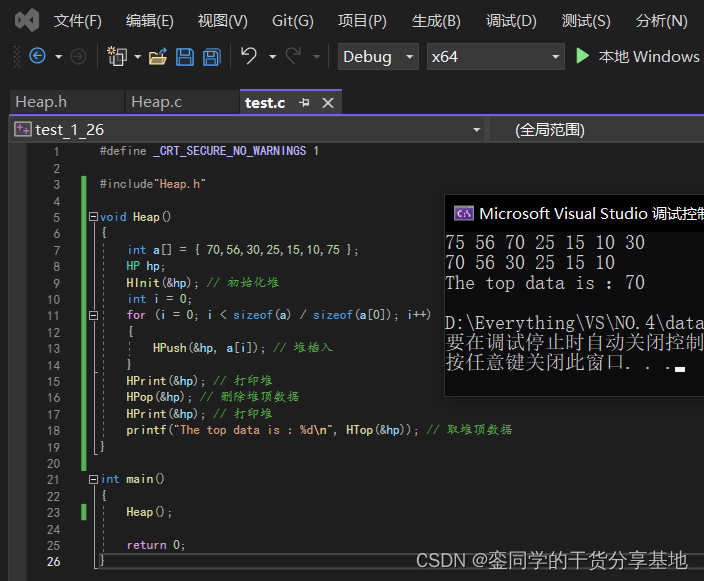
  • 测试取堆顶数据接口功能实现：

⑤.堆中数据个数：

  • 查看堆中的数据个数操作很简单，在判断传入指针非空后，直接返回 p->size 的值，即堆中保存的数据数量即可。
int HSize(HP* p)
{
	if (p == NULL)
	{
		printf("Size Get Error!\n");
		return;
	}
	return p->size;
}
  • 测试数据个数获取接口功能实现：

⑥.堆的判空：

  • 堆的判空操作与队列完全相同，这里不再作过多阐述。
//堆数据判空：
bool HEmpty(HP* p)
{
	if (p == NULL)
	{
		printf("Empty Error!\n");
		exit;
	}
	return p->size == 0;
}

⑦.堆的销毁：

  • 堆的销毁与队列完全相同，这里不再作过多阐述。
void HDestroy(HP* p)
{
	if (p == NULL)
	{
		printf("Destroy Error!\n");
		return;
	}
	free(p->a);
	p->a = NULL;
	p->size = p->capacity = 0;
}
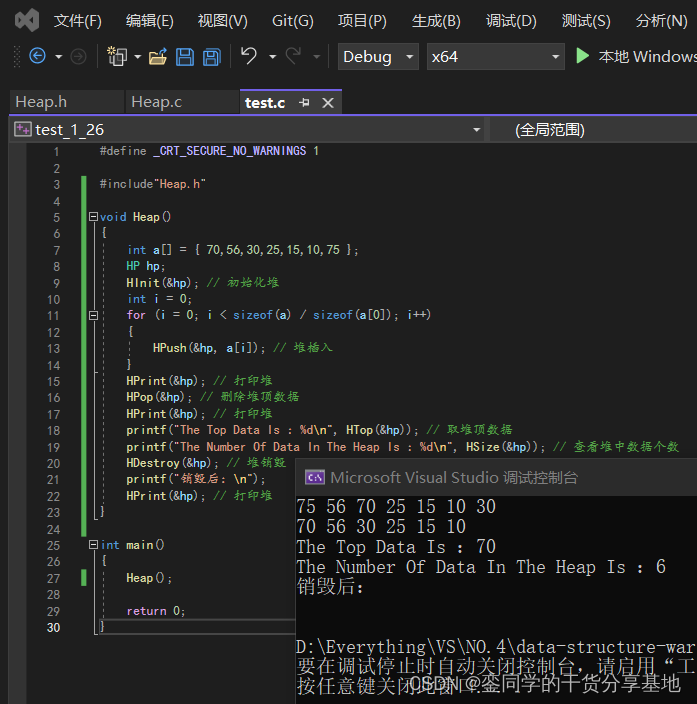
  • 测试销毁接口功能实现：

4.堆实现全部代码：

①.Heap.h：

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int HDataType;

typedef struct Heap
{
	HDataType* a;
	int size;
	int capacity;
}HP;

void HInit(HP* p); // 堆的初始化
void HPrint(HP* p); // 打印堆
void HPush(HP* p, HDataType x); // 堆插入
void HPop(HP* p); // 堆顶数据删除
HDataType HTop(HP* p); // 取堆顶数据
int HSize(HP* p); // 堆中数据个数
bool HEmpty(HP* p); // 堆数据判空
void HDestroy(HP* p); // 堆销毁

②.Heap.c：

#define _CRT_SECURE_NO_WARNINGS 1

#include"Heap.h"

//堆的初始化：
void HInit(HP* p)
{
	if (p == NULL)
	{
		printf("Init Error!\n");
		exit;
	}
	p->a = NULL;
	p->size = p->capacity = 0;
}

//打印堆：
void HPrint(HP* p)
{
	if(p==NULL)
	{
		printf("Printf Error!\n");
		return;
	}
	int i = 0;
	for (i = 0; i < p->size; ++i)
	{
		printf("%d ", p->a[i]);
	}
	printf("\n");
}

//向上调整算法：
void AdJustUp(int* a,int n,int child)
{
	if (a == NULL)
	{
		printf("AdJustUp Error!\n");
		return;
	}
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//大根堆节点交换(判断小根堆秩序将">"换为"<"即可)：
		if (a[child] > a[parent])
		{
			HDataType tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;
			//重复向上走：
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

//堆插入：
void HPush(HP* p, HDataType x)
{
	if (p == NULL)
	{
		printf("Push Error!\n");
		return;
	}
	if (p->size == p->capacity)
	{
		//插入前扩容：
		size_t newCapacity = (p->capacity == 0) ? 4 : (p->capacity * 2);
		HDataType* tmp = realloc(p->a, sizeof(HDataType) * newCapacity);
		//判断扩容结果：
		if (tmp == NULL)
		{
			printf("Capacuty Get Error!\n");
			return;
		}
		//增容成功后的处理：
		else
		{
			p->a = tmp;
			p->capacity = newCapacity;
		}
	}
	//插入数据：
	p->a[p->size] = x;
	p->size++;
	//向上调整：
	AdJustUp(p->a, p->size, p->size - 1);
}

//向下调整算法：
void AdJustDown(int* a, int n, int parent)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		//选出两孩子中的较小孩子(需要考虑边界，防止越界访问)：
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;
		}
		//向下调整：
		if (a[child] > a[parent])
		{
			int* tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//堆顶数据删除：
void HPop(HP* p)
{
	if (p == NULL)
	{
		printf("Pop Error!\n");
		return;
	}
	//堆数据判空：
	if (HEmpty(&p) == 1)
	{
		printf("Is Null !\n");
		return;
	}
	HDataType* tmp = p->a[0];
	p->a[0] = p->a[p->size - 1];
	p->a[p->size - 1] = tmp;
	p->size--;
	AdJustDown(p->a, p->size - 1, 0);
}

//取堆顶数据：
HDataType HTop(HP* p)
{
	if (p == NULL)
	{
		printf("Top Get Error!\n");
		return;
	}
	//堆数据判空：
	if (HEmpty(&p) == 1)
	{
		printf("Is Null !\n");
		exit;
	}
	return p->a[0];
}

//堆中数据个数：
int HSize(HP* p)
{
	if (p == NULL)
	{
		printf("Size Get Error!\n");
		return;
	}
	return p->size;
}

//堆数据判空：
bool HEmpty(HP* p)
{
	if (p == NULL)
	{
		printf("Empty Error!\n");
		exit;
	}
	return p->size == 0;
}

//堆销毁：
void HDestroy(HP* p)
{
	if (p == NULL)
	{
		printf("Destroy Error!\n");
		return;
	}
	free(p->a);
	p->a = NULL;
	p->size = p->capacity = 0;
}

③.test.c：

#define _CRT_SECURE_NO_WARNINGS 1

#include"Heap.h"

void Heap()
{
	int a[] = { 70,56,30,25,15,10,75 };
	HP hp;
	HInit(&hp); // 初始化堆
	int i = 0;
	for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
	{
		HPush(&hp, a[i]); // 堆插入
	}
	HPrint(&hp); // 打印堆
	HPop(&hp); // 删除堆顶数据
	HPrint(&hp); // 打印堆
	printf("The Top Data Is ：%d\n", HTop(&hp)); // 取堆顶数据
	printf("The Number Of Data In The Heap Is ：%d\n", HSize(&hp)); // 查看堆中数据个数
	HDestroy(&hp); // 堆销毁
	printf("销毁后：\n");
	HPrint(&hp); // 打印堆
}

int main()
{
	Heap();

	return 0;
}

📕总结📕：

        今天我们完整地认识、了解、学习了二叉树顺序存储结构的相关知识，并且对二叉树顺序存储的实例——堆的各接口功能进行了研究与实现。至此，关于二叉树的顺序存储的知识我们就全部学习完毕了，希望各位小伙伴们仍能多多翻阅，多多动手练习，不断巩固基础磨练自己的编程技术。下节课中我们将要学习链式存储结构的相关知识，各位小伙们下去以后，若有多余的精力，可以提前进行预习，以便于接下来更好的理解二叉树的链式存储结构的各种功能接口的实现。

        🔥🔥当我们远离了言语与是非，我们的一切存在也就真实地显露了其本来的价值🔥🔥

        更新不易，辛苦各位小伙伴们动动小手，👍三连走一走💕💕 ~ ~ ~  你们真的对我很重要！最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/180300.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

离线用户召回定时更新系列二

离线用户召回定时更新系列二

3.6.3 特征处理原则 离散数据 one-hot编码连续数据 归一化图片/文本 文章标签/关键词提取embedding3.6.4 优化训练方式 使用Batch SGD优化 加入正则化防止过拟合 3.6.5 spark LR 进行预估 目的&#xff1a;通过LR模型进行CTR预估步骤&#xff1a; 1、需要通过spark读取HIVE外…
阅读更多...
Nacos学习笔记【part1】安装与注册服务

Nacos学习笔记【part1】安装与注册服务

一、概述与安装 Nacos 是是一个构建云原生应用的动态服务发现、配置管理和服务管理平台&#xff0c;用于发现、配置和管理微服务&#xff0c;提供了一组简单易用的特性集&#xff0c;快速实现动态服务发现、服务配置、服务元数据及流量管理。 Nacos 更敏捷和容易地构建…
阅读更多...
分享136个ASP源码，总有一款适合您

分享136个ASP源码，总有一款适合您

ASP源码 分享136个ASP源码&#xff0c;总有一款适合您 下面是文件的名字&#xff0c;我放了一些图片&#xff0c;文章里不是所有的图主要是放不下...&#xff0c; 136个ASP源码下载链接&#xff1a;https://pan.baidu.com/s/11db_K2QXns5pm8vMZBVPSw?pwds0lb 提取码&#x…
阅读更多...
js 文字转语音 api SpeechSynthesisUtterance

js 文字转语音 api SpeechSynthesisUtterance

SpeechSynthesisUtterance基本介绍 SpeechSynthesisUtterance是HTML5中新增的API,用于将指定文字合成为对应的语音.也包含一些配置项,指定如何去阅读(语言,音量,音调)等 官方文档地址&#xff08;https://developer.mozilla.org/zh-CN/docs/Web/API/SpeechSynthesisUtterance…
阅读更多...
【JavaEE初阶】第七节.多线程(基础篇)单例模式（案例一）

【JavaEE初阶】第七节.多线程(基础篇)单例模式（案例一）

欢迎大家跟我一起来学习有关多线程的有关内容&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01; 文章目录 前言 一、单例模式的概念 二、单例模式的简单实 2.1 饿汉模式 2.2 懒汉模式 总结 前言…
阅读更多...
搭建Linux环境

搭建Linux环境

学习Linux之前&#xff0c;我们首先需要在电脑上搭建Linux操作系统环境。 就好比说你买了一台电脑&#xff0c;需要使用Windows10操作系统&#xff0c;那么首先应该安装Windows操作系统&#xff08;刚买的电脑会引导你一步一步的安装&#xff09;。 一、Linux环境搭建的三种方式…
阅读更多...
数据结构 第三章 栈和队列(队列)

数据结构 第三章 栈和队列(队列)

感谢&#xff1a;点击收听 1 基本知识点 1、允许删除的一端称为队头(front) 2、允许插入的一端称为队尾(rear) 3、当队列中没有元素时称为空队列 4、顺序队列&#xff1a; 1 使用顺序表来实现队列 2 两个指针分别指向队列的前端和尾端 **3 如果队列的大小为MaxSize个,那么元…
阅读更多...
什么是倒排表（倒排索引）

什么是倒排表（倒排索引）

这种搜索引擎的实现常常用的就是倒排的技术 文档(Document)&#xff1a;一般搜索引擎的处理对象是互联网网页&#xff0c;而文档这个概念要更宽泛些&#xff0c;代表以文本形式存在的存储对象&#xff0c;相比网页来说&#xff0c;涵盖更多种形式&#xff0c;比如Word&#xff…
阅读更多...
在Mac下如何创建文件

在Mac下如何创建文件

相比于windows中创建Mac是比较复杂的 第一步&#xff1a;打开启动台&#xff0c;依次打开「启动台-其他-自动操作」&#xff0c;可以按住「 Command 空格」直接搜索「自动操作」程序。 第二步&#xff1a;打开之后在「选取文稿类型」选项时&#xff0c;选择「快速操作」&#…
阅读更多...
工地车辆未冲洗识别抓拍系统 yolov5网络

工地车辆未冲洗识别抓拍系统 yolov5网络

工地车辆未冲洗识别抓拍系统通过yolov5网络深度算法学习模型&#xff0c;自动对画面中每辆进出车辆的清洗实现自动识别判定。如果识别到车辆冲洗不合格&#xff0c;就会自动进行抓拍并将违规车辆信息回传。目标检测架构分为两种&#xff0c;一种是two-stage&#xff0c;一种是o…
阅读更多...
「兔了个兔」看我如何抓取兔兔图片到本地（附源码）

「兔了个兔」看我如何抓取兔兔图片到本地（附源码）

&#x1f482;作者简介&#xff1a; THUNDER王&#xff0c;一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学会计学专业大二本科在读&#xff0c;同时任汉硕云&#xff08;广东&#xff09;科技有限公司ABAP开发顾问。在学习工作中&#xff0c;我通常使用偏后…
阅读更多...
如何在IDEA中使用Maven构建Java项目？Maven的使用详细解读

如何在IDEA中使用Maven构建Java项目？Maven的使用详细解读

文章目录1. 前言2. IDEA 中配置 Maven 环境3. Maven 的坐标问题4. IDEA 中创建 Maven 项目5. IDEA 中导入 Maven 项目6. 安装插件7. 依赖管理8. 依赖范围6. 总结Java编程基础教程系列1. 前言 前面在如何使用 Maven 构建 Java 项目一文中&#xff0c;我们一直在命令行中执行构建…
阅读更多...
LabVIEW什么是实时操作系统(RTOS)

LabVIEW什么是实时操作系统(RTOS)

LabVIEW什么是实时操作系统(RTOS)一般而言&#xff0c;操作系统的任务是管理计算机的硬件资源和应用程序。实时操作系统会执行这些任务&#xff0c;但是运行时间精度和可靠度都极高。在实际应用中&#xff0c;有的系统失常代价高昂&#xff0c;甚至会引起安全事故。这时&#x…
阅读更多...
成为提示专家，AI艺术杂志：AI Unleashed 第一期

成为提示专家，AI艺术杂志：AI Unleashed 第一期

shadow最近发现了一期AI艺术的杂志。名称叫 AI Unleashed&#xff0c;是一本深入探索 AI 和想象力的杂志。每期杂志都将填满精彩的 AI 艺术&#xff0c;激发你的好奇心&#xff0c; 让你更加了解最新的 AI 技术&#xff0c;以及它如何改变现有工作流和我们对艺术和技术的看法。…
阅读更多...
LVS+keepalived（双主）+Nginx实现高可用负载均衡

LVS+keepalived（双主）+Nginx实现高可用负载均衡

#为什么采用双主架构&#xff1a; 单主架构只有一个keepalived对外提供服务&#xff0c;该主机长期处于繁忙状态&#xff0c;而另一台主机却很空闲&#xff0c;利用率低下 #双主架构的优点&#xff1a; 即将两个或以上VIP分别运行在不同的keepalived服务器&#xff0c;以实现…
阅读更多...
C++11使用线程类thread的方法

C++11使用线程类thread的方法

C11 之前&#xff0c;C 语言没有对并发编程提供语言级别的支持。如果需要使用线程&#xff0c;windows系统需要使用CreateThread函数创建线程&#xff0c;而linux需要使用pthread库使用线程。C11 中增加了线程以及线程相关的类&#xff0c;很方便地支持了并发编程。由于可以跨平…
阅读更多...
活动星投票十大商业品牌网络评选微信的投票方式线上免费投票

活动星投票十大商业品牌网络评选微信的投票方式线上免费投票

“十大商业品牌”网络评选投票_线上系统免费投票_功能齐全的视频投票_在线投票免费小程序用户在使用微信投票的时候&#xff0c;需要功能齐全&#xff0c;又快捷方便的投票小程序。而“活动星投票”这款软件使用非常的方便&#xff0c;用户可以随时使用手机微信小程序获得线上投…
阅读更多...
CV学习笔记-VGG

CV学习笔记-VGG

VGG 1. 常见的卷积神经网络 VGG属于一种经典的卷积神经网络结构&#xff0c;其出现在AlexNet之后&#xff0c;由于AlexNet的突破证实了卷积神经网络的可行性&#xff0c;VGG的思路主要是将网络层数加深&#xff0c;从某种意义上说&#xff0c;网络层数的加深可以粗略地认为考虑…
阅读更多...
编译原理学习笔记14——属性文法与语法制导翻译1

编译原理学习笔记14——属性文法与语法制导翻译1

编译原理学习笔记14——属性文法与语法制导翻译114.1 属性文法14.2 属性计算14.1 属性文法 属性文法 综合属性 自下而上传递信息语法规则&#xff1a;根据右 部候选式中的符号 的属性计算左部被 定义符号的综合属性语法树&#xff1a;根据子结 点的属性和父结点 自身的属性…
阅读更多...
【日常系列】LeetCode《30·动态规划总结》

【日常系列】LeetCode《30·动态规划总结》

动态规划总结 线性动态规划问题总结 打家劫舍总结 最大子数组和总结 dp[i] 依赖于前面一个或者两个状态 dp[i] 依赖于前面多个状态 注意&#xff1a;子序列可以不连续 dp[i] 带有一个或者多个维度 输入为两个数组或者两个字符串 lc 10【剑指 19】【top100】&#xff1a;正…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023