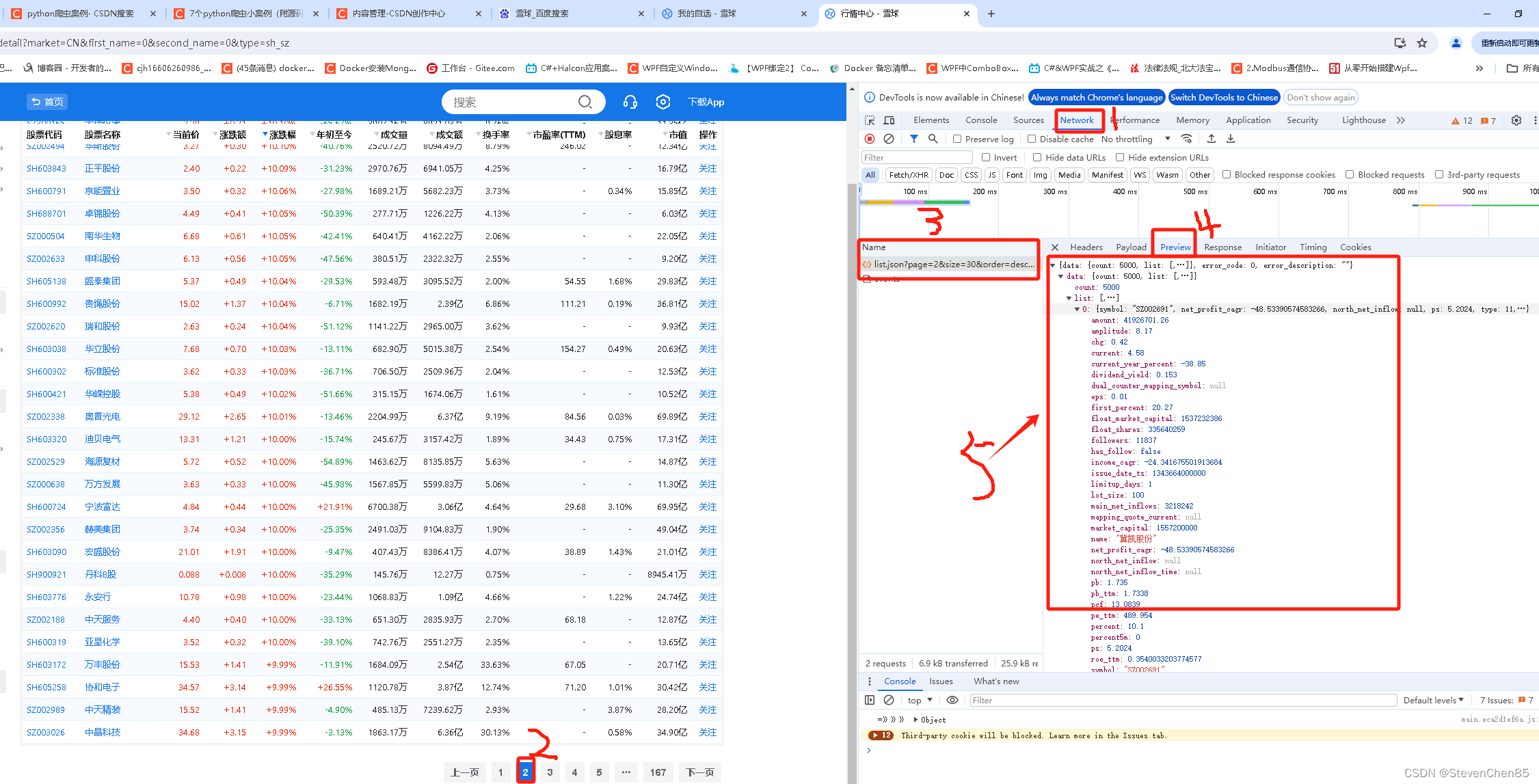
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
Problem - 551D - Codeforces
二、解题报告
1、思路分析
今天LATEX怎么不好用了
数据量很大,应该要用O(log) 或者 O(1)的的算法
按位考虑进行dp,计算k每位的方案数累乘即可,详细看下面的LATEX
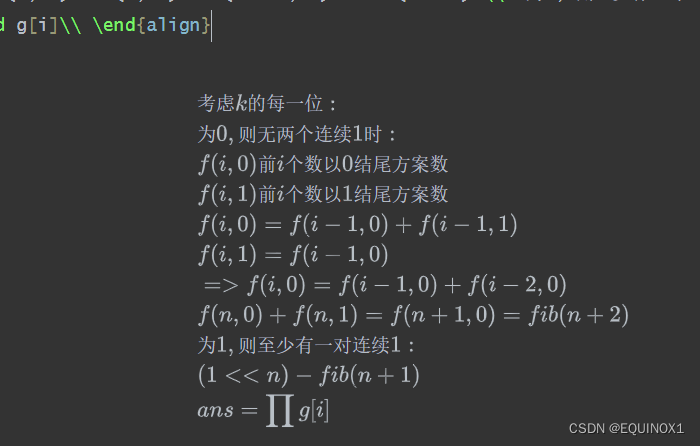
2、复杂度
时间复杂度: O(L + 8 * log(n)) 空间复杂度:O(L)
3、代码详解
#include <bits/stdc++.h>
using PII = std::pair<int, int>;
using i64 = long long;
using i128 = __int128;
std::ostream& operator<< (std::ostream& out, i128 x) {
std::string s;
while (x) s += ((x % 10) ^ 48), x /= 10;
std::reverse(s.begin(), s.end());
return out << s;
}
int qp(int a, i64 b, int p) {
int res = 1;
while (b) {
if (b & 1) res = 1LL * res * a % p;
a = 1LL * a * a % p, b >>= 1;
}
return res;
}
int P;
template<typename T>
class Matrix {
private:
T m, n;
std::vector<std::vector<T>> g;
public:
Matrix(int _m, int _n) : m(_m), n(_n), g(m, std::vector<T>(n)) {}
void init1 () {
for (int i = 0; i < m; i ++ ) g[i][i] = 1;
}
Matrix(const Matrix& x) : m(x.m), n(x.n), g(x.g) {}
void init (const std::vector<std::vector<T>> _g) {
g = _g;
}
Matrix<T> operator * (const Matrix<T>& x) const {
Matrix<T> res(m, x.n);
for (int i = 0; i < m; i ++ )
for (int k = 0; k < n; k ++ )
for (int j = 0; j < n; j ++ )
res.g[i][j] = (res[i][j] + 1LL * g[i][k] * x[k][j] % P) % P;
return res;
}
const std::vector<T>& operator [] (int i) const {
return g[i];
}
Matrix<T> qp(i64 b) {
Matrix<T> res(m, n), a(*this);
res.init1();
while (b) {
if (b & 1) res = res * a;
a = a * a, b >>= 1;
}
return res;
}
};
i64 fib(i64 n) {
if (n <= 2) return 1;
Matrix<i64> a(1, 2) ,b(2, 2);
std::vector<std::vector<i64>> aa { { 1, 1 } }, bb { { 1, 1 }, { 1, 0 } };
a.init(aa), b.init(bb);
return (a * b.qp(n - 1))[0][0];
}
void solve() {
i64 N, K, L, M;
std::cin >> N >> K >> L >> M;
P = M;
if (M == 1 || (L < 63 && 1LL << L <= K)) {
std::cout << 0;
return;
}
if (L == 0) {
if (K == 0) std::cout << 1;
else std::cout << 0;
return;
}
std::vector<int> d(L);
for (int i = 0; i < L; i ++)
d[i] = (K >> i & 1);
i64 f = fib(N + 1), q = ((qp(2, N, M) - f) % M + M) % M, res = 1;
for (int i = 0; i < L; i ++) {
if (d[i])
res = res * q % M;
else
res = res * f % M;
}
std::cout << res;
}
int main () {
std::ios::sync_with_stdio(false); std::cin.tie(0); std::cout.tie(0);
int _ = 1;
// std::cin >> _;
while (_ --)
solve();
return 0;
}
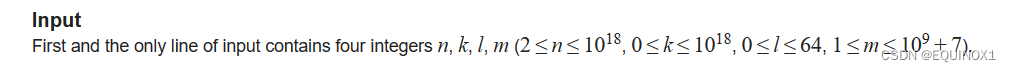



![[AIGC] SpringBoot的自动配置解析](https://img-blog.csdnimg.cn/direct/df74428b20fc4e7287de25ffc2995c55.png)