1、选择排序
1.1 基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,放在序列的起始位置,直到全部待排序的数据元素排完就停止 。
1.2 直接选择排序
排序思想:
①在元素集合array[i]--array[n-1]中选择数值最大(小)的数据元素。
②若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换,使最大(最小)的元素来到数据的最后(开始)。
③在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素。
动图演示:
动图解释:
①遍历区间 [ 0, n-1 ] 的所有数,选出最小的数放到我们所遍历区间的最左端,第一次遍历区间最左端是0。
②遍历区间 [ 1, n-1 ] 的所有数,选出最小的数放到我们所遍历区间的最左端,第而二次遍历区间最左端是1。
③不断重复上述步骤,直至区间内的元素个数为一个时,停止遍历。
代码实现:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void SelectSort2(int* a, int n)
{
int begin = 0, end = n - 1;
// 区间为 [begin , end]
while (begin < end) // 当 begin == end 时,表明区间内还剩一个元素,停止遍历
{
// 假设最小值都为区间的最左端元素
int mini = begin;
for (int i = begin + 1; i <= end; i++)
{
// 在区间内遇到更小的数就更新 mini
if (a[i] < a[mini])
mini = i;
}
// 第一次遍历结束,mini位置的值为该区间的最小值
Swap(&a[begin], &a[mini]);// 将最小值放到该区间的最左端
// 缩小区间的长度
begin++;
}
}
代码优化:
实际上在每一次的遍历中,我们不仅可以选出最小值放到区间的最左端,同时我们还可以选出最大值放到区间的最右端,这样可以减少我们的遍历次数。
优化代码实现:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
// 区间为 [begin , end]
while(begin < end) // 当 begin == end 时,表明区间内还剩一个元素,停止遍历
{
// 假设最大值与最小值都为区间最左端元素
int maxi = begin, mini = begin;
for (int i = begin + 1; i <= end; i++)
{
// 在区间内遇到更大的数就更新 maxi
if (a[i] > a[maxi])
maxi = i;
// 在区间内遇到更小的数就更新 mini
if (a[i] < a[mini])
mini = i;
}
// 第一次遍历结束,maxi、mini位置的值为该区间的最大值与最小值
Swap(&a[begin], &a[mini]);// 将最小值放到该区间的最左端
// 当我们的区间最大值位于 begin 位置时,即maxi = begin时
//因为我们上面的交换,导致begin位置的值已经被换到 mini 位置
//所以现在最大值的下标是 mini
if (maxi == begin)//当最大的数据在 begin 位置时,
maxi = mini;
Swap(&a[end], &a[maxi]); // 将最大值放到该区间的最右端
// 缩小区间的长度
begin++;
end--;
}
}
直接选择排序的特性总结:
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
不稳定的原因:当数组已经接近有序或已经完全有序时,每一次还是会进行找大找小,这样就会导致时间上的巨大浪费。
1.3 堆排序
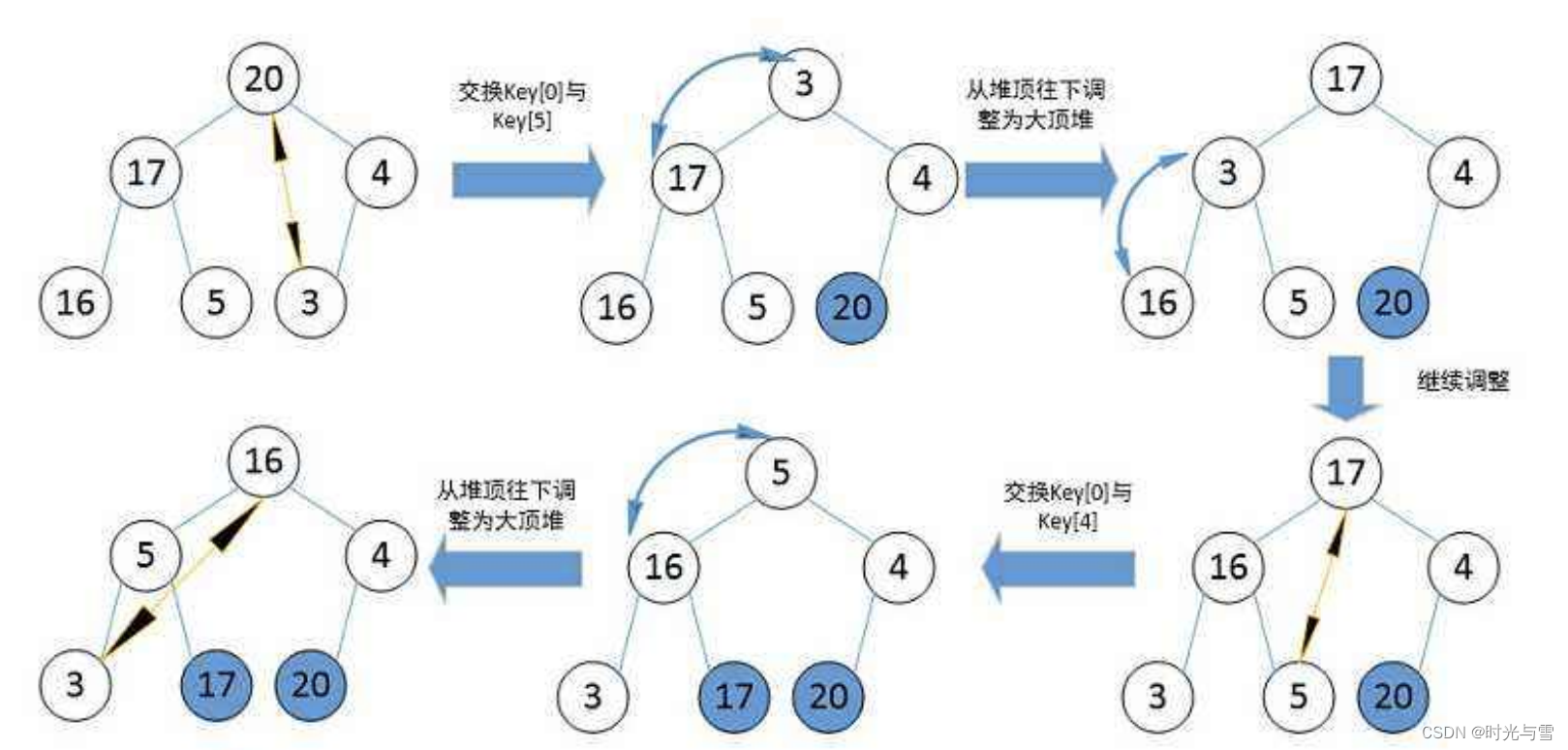
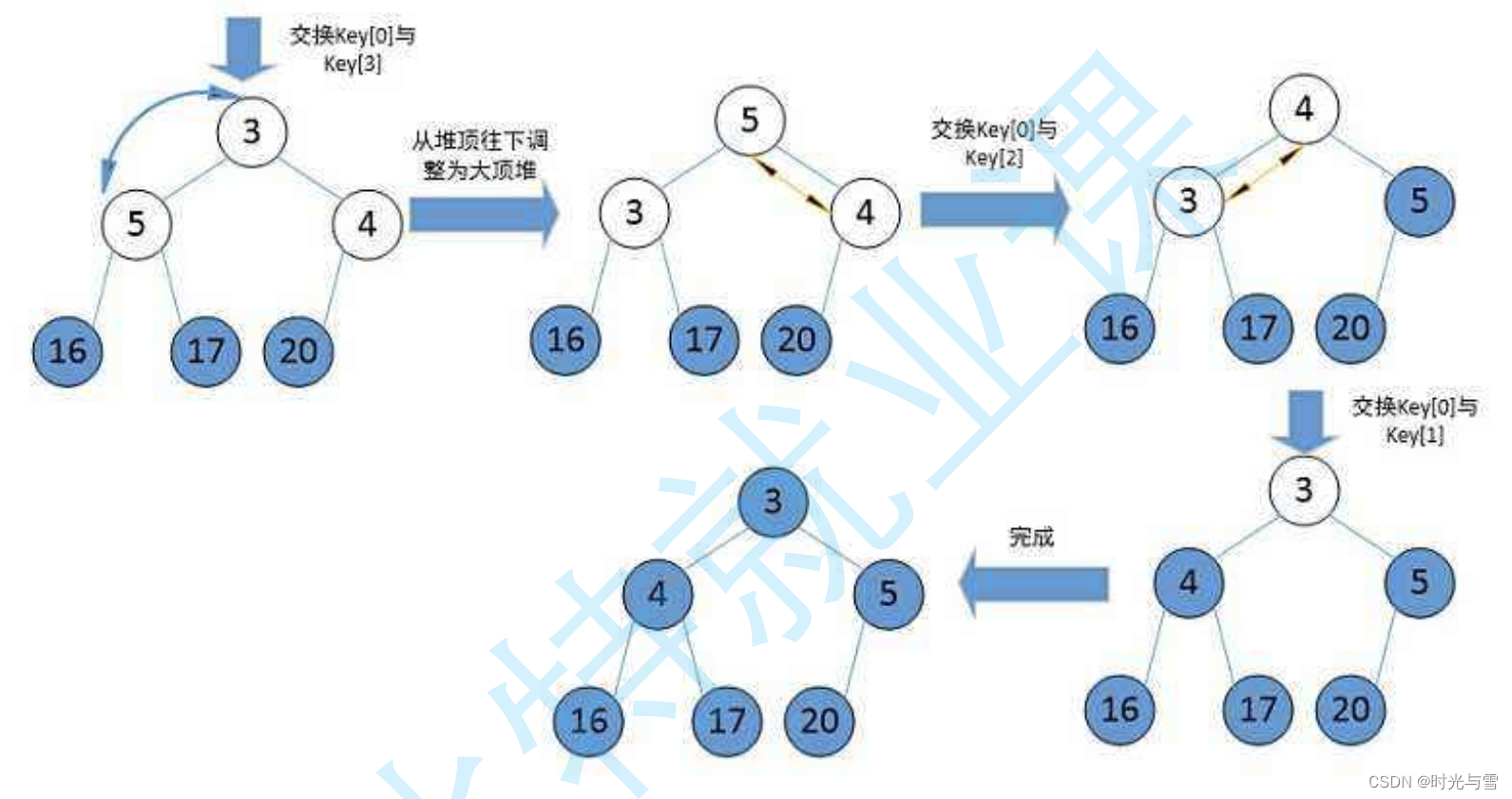
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种,但相较于直接选择排序来说提升了许多 。它是通过堆(完全二叉树)来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。(如果还未学习堆的同学,可以移步到我的上一篇文章,里面有堆的详细介绍)
堆排序的排序思想:
如果我们想利用堆排升序:
①首先我们需要建立一个有N个数据的大堆;
②将堆顶的数据(最大)与最后一个数据(下标是N-1)交换,此时我们最大的数据就来到了最后(N-1的位置),这时我们就不用再需要去考虑最后一个元素了,因为最后一个元素已经是最大;
③再对前N-1个数据再次进行堆排序即可。
注意:此刻交换到堆顶的数据并不一定满足大堆的性质,所以还需要对堆顶的数据进行向下调整,使得满足大堆的性质。
示意图:
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustDown(HPDataType* a, int size,int parent)
{
int child = 2 * parent + 1;
while (child < size)
{
if ((child + 1) < size && a[child + 1] > a[child]) // 找出左右孩子中较大一个
{
child++;
}
if (a[parent] < a[child]) // 如果孩子更大就交换,并且更新父节点与孩子节点
{
Swap(&a[parent], &a[child]);
parent = child;
child = 2 * parent + 1;
}
else // 如果父节点更大表明不用再交换了 ,跳出循环
{
break;
}
}
}
void HeapSort(int* a, int n)
{
// 利用向下调整算法建立一个大堆
for (int i = (n - 1-1) / 2; i >= 0; i--) // n-1 是最后一个节点,(n-1-1)/2就是第一个非叶子节点
{
AdjustDown(a, n,i);
}
int end = n-1; // end 表示最后一个元素的下标
while(end>0) //如果数据个数大于1个,才进行排序
{
Swap(&a[0], &a[end]); // 堆顶与最后一个元素进行交换
AdjustDown(a, end, 0); // 将堆顶的数据向下调整
end--; // 每排好一个就不用再考虑最后一个元素,相当与堆的数据减少一个
}
}堆排序的特性总结:
1. 堆排序使用堆来选数,效率就高了很多
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
不稳定的原因与直接选择排序类似,当数组已经有序或接近有序时,还需要建堆从而导致已经有序或接近有序的数据又会被从新打乱进行排序,同样会造成时间上的浪费。



![[职场] 硬件研发是什么职业 #职场发展#其他](https://img-blog.csdnimg.cn/img_convert/b514ef3a90a680b4c12ed0adeb53c82f.png)