题目（leecode T106）：

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

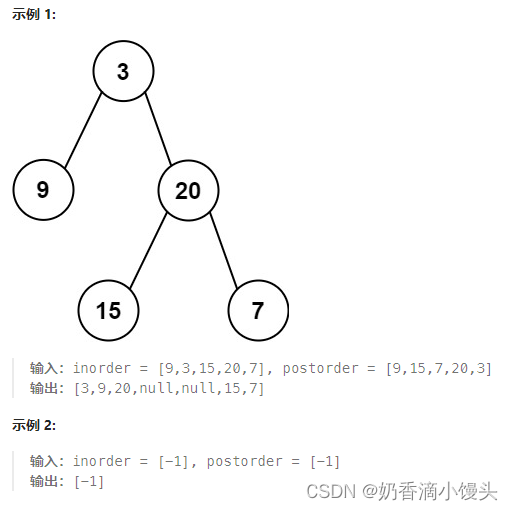
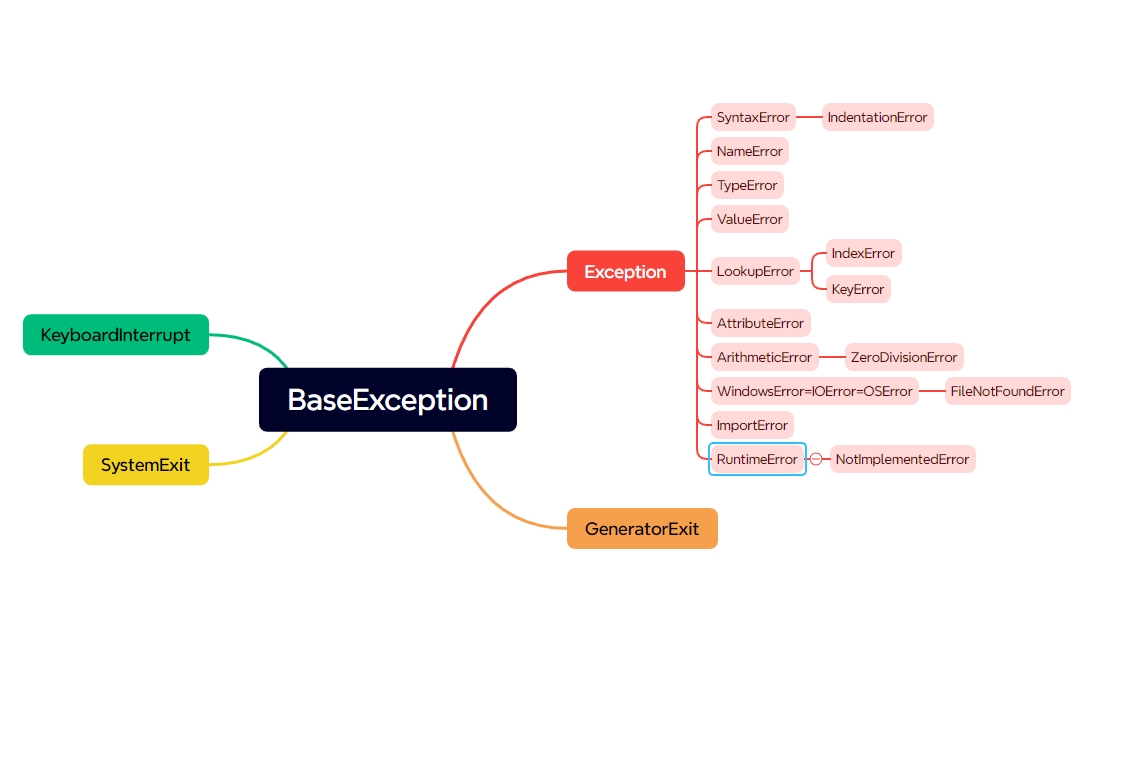
方法：本题要通过中序遍历和后序遍历确定唯一一个二叉树，基本理论方法是先从后序遍历中去除最后一个节点，该节点就是当前树的根节点，再去中序遍历中找到该节点，该节点左边的值就是左子树的值，右边的值就是右子树的值，将中序遍历切分为左中序数组与右中序数组。再切割右子树数组，因为中序遍历与后序遍历的长度肯定是一致的，且左右部分数组的长度也是一致的，我们可以通过已经获得的左中序遍历数组来获得左后续遍历数组。通过这样的切割获得了四个数组：左中序数组，左后序数组，右中序数组和右后序数组。这样的一轮递归就已经完成了，剩下我们再将左中序数组与左后序数组传入递归函数得到当前root的左子树，将右中序数组与右后序数组传入递归函数得到当前root的右子树。最后返回root就完成了递归。

class Solution {
private:
    TreeNode* traversal(vector<int>& inorder, vector<int>& postorder){
        if(postorder.size() == 0) return NULL;

        int rootValue = postorder[postorder.size() - 1];                                  //找到根节点，即后序遍历的最后一个值
        TreeNode* root = new TreeNode(rootValue);

        if(postorder.size() == 1) return root;

        int delimiterIndex = 0;                                                          //在中序遍历中找到切割节点
        for(delimiterIndex; delimiterIndex < inorder.size(); delimiterIndex++){
            if(inorder[delimiterIndex] == rootValue) break;
        }
        vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);       //切割中序数组
        vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end());

        postorder.resize(postorder.size() - 1);                                              //去掉后序遍历最后一个值

        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());    //切割后序遍历
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        root->left = traversal(leftInorder, leftPostorder);                                   //递归左子树
        root->right = traversal(rightInorder, rightPostorder);                                //递归右子树

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};