一、单选题
第1题
在数组中,数组名表示( ).
A:数组第1个元素的首地址
B:数组第2个元素的首地址
C:数组所有元素的首地址,
D:数组最后1个元素的首地址
答案:A
数组名是一个地址,指向第一个元素
第2题
下列叙述中正确的是( ).
A:顺序存储结构的存储一定是连续的,链式存储结构的存储空间不一定是连续的
B:顺序存储结构只针对线性结构,链式存储结构只针对非线性结构
C:顺序存储结构能存储有序表,链式存储结构不能存储有序表
D:链式存储结构比顺序存储结构节省存储空间
答案:A
数组和链表,一个地址空间连续一个地址空间不一定连续。
第3题
下列排序方法中,最坏情况下比较次数最少的是( ).
A:冒泡排序
B:简单的选择排序
C:直接插入排序
D:堆排序
答案:D
按照时间复杂度分析 A、B、C 都是O(n^logn)级别
第4题
下列表达式正确的是( ).
A:9++
B:(x+y)++
C:c+++c+++c++
D:++(a-b–)
答案:C
9是一个常量,常量不能自增自减,而(x+y)和下面的(a-b–)都是作为一种只读内存区存在的,所以都不能进行自增自减操作。
第5题
针对以下代码,判断下列说法哪个是正确的( ).
const char str1[]=“abc”;
const char str2[] =“abc”;
const char *p1 =“abc”;
const char *p2 =“abc”;
A:str1和str2地址不同,P1和P2地址相同
B:str1和str2地址相同,P1和P2地址相同
C:str1和str2地址不同,P1和P2地址不同
D:str1和str2地址相同,P1和P2地址不同
答案:C
二、编程题
第6题:求阶乘
提示信息:
阶乘定义:一个正整数的阶乘是所有小于及等于该数的正整数的乘积。
例如:3的阶乘6(也就是123的结果)
例如:5的阶乘120(也就是1234*5的结果)
题目描述:
输入一个正整数N(3<=N<=20),输出1到N之间(包含1和N)所有正整数阶乘的和。
例如:输入为3,1的阶乘为1,2的阶乘为2,3的阶乘为6,1+2+6=9,则输出9。
输入描述
输入一个正整数N(3<=N<=20)
输出描述
输出1到N之间(包含1和N)所有正整数阶乘的和
样例输入
3
样例输出
9
答案:
参考代码一:
#include <iostream>
using namespace std;
long long sum=0;
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
int f=1;
for(int j=1;j<=i;j++){
f*=j;
}
sum+=f;
}
cout<<sum;
return 0;
}
参考代码二:
#include <iostream>
using namespace std;
long long f[21],sum=1;
int n;
int main(){
cin>>n;
f[1]=1;
for(int i=2;i<=n;i++){
f[i]=f[i-1]*i;
sum+=f[i];
}
cout<<sum;
return 0;
}
第7题:判断偶数
题目描述:
输入两个不相等的四位正整数N(1000<=N<=9999)和M(1000<=M<=9999),其中N<M,中间以一个空格隔开,输出N与M之间(包含N和M)所有满足要求的正整数且正整数之间以一个英文逗号隔开。
要求每个正整数的各个位上的数都为偶数(注:0为偶数)
输入描述
在一行输入两个不相等的四位正整数N和M(N和M之间以一个空格隔开)
输出描述
输出N与M之间(包含N和M)所有满足要求的正整数且正数之间以一个英文逗号隔开
样例输入
4000 4008
样例输出
4000,4002,4004,4006,4008
答案:
参考代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,flag;
bool check(int x){
while(x){
if(x%10%2!=0) return false;
x/=10;
}
return true;
}
int main(){
cin>>n>>m;
for(int i=n;i<=m;i++){
if(check(i)){
if(flag)cout<<',';
else flag=1;
cout<<i;
}
}
return 0;
}
第8题:计数
题目描述
输入一个正整数n(1 <=n<= 1000),统计从1到n之间(包含1和n)所有正整数中,0,1,2,3,4,5,6,7,8,9的数字分别出现的次数,且按样例分行输出(按0到9顺序输出,英文逗号前为0到9的数字,逗号后为该数字出现的次数)。
例如:n为12,那么1到n之间所有的正整数有1,2,3,4,5,6,7,8,9,10,11,12.
在12个正整数中数字0出现了1次数字1出现了5次数字2出现了2次数字2,3,4,5,6,7,8,9分别出现了1次。
输入描述
输入一个正整数n
输出描述
0,0出现的次数
1,1出现的次数
2,2出现的次数
………
9,9出现的次数
样例输入
10
样例输出
0,1
1,2
2,1
3,1
4,1
5,1
6,1
7,1
8,1
9,1
答案:
参考代码一:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> count(10, 0); // 用于统计每个数字出现的次数
for (int i = 1; i <= n; i++) {
int num = i;
while (num > 0) {
int digit = num % 10; // 获取当前数字的最低位
count[digit]++; // 对应数字的次数加一
num /= 10; // 去掉最低位
}
}
for (int i = 0; i <= 9; i++) {
cout << i << "," << count[i] << endl;
}
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
int n, cnt[10];
void getans(int x) {
for (; x; x /= 10)
++cnt[x % 10];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i)
getans(i);
for (int i = 0; i < 10; ++i)
cout << i << ',' << cnt[i] << '\n';
return 0;
}
评分标准:
10分:能正确输出一组数据;
20分:能正确输出两组数据;
20分:能正确输出三组数据。
第9题:找公共子串
题目描述:
分行输入两个字符串(2<=字符串长度<=100),找出两个字符串中最大的公共子串,然后将公共子串及公共子串的长度分行输出
例如:输入两个宇串为abcdab和baabcd,其最大的公共子串为"abcd",子串长度为4.
输入描述
第一行输入一个字符串
第二行输入一个字符串
输出描述
第一行输出最大公共子串
第二行输出最大公共子串长度
样例输入
abcdab
baabcd
样例输出
abcd
4
答案:
参考代码一:
#include <bits/stdc++.h>
using namespace std;
string a, b;
int main() {
cin >> a >> b;
for (int l = a.size(); l >= 1; l--) {
for (int i = 0; i <= a.size() - l; i++) {
if (b.find(a.substr(i, l)) < b.size()) {
cout << a.substr(i, l) << endl;
cout << l;
return 0;
}
}
}
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
string s1, s2;
int st, len;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> s1 >> s2;
int l1 = s1.size(), l2 = s2.size();
for (int i = 0; i < l1; ++i) {
for (int j = 0; j < l2; ++j) {
for (int k = 1; i + k - 1 < l1 && j + k - 1 < l2; ++k) {
if (s1[i + k - 1] != s2[j + k - 1])
break;
if (k > len) {
len = k;
st = i;
}
}
}
}
for (int i = 0; i < len; ++i)
cout << s1[i + st];
cout << '\n' << len << '\n';
return 0;
}
评分标准:
10分:能正确输出一组数据;
20分:能正确输出两组数据;
20分:能正确输出三组数据。
第10题:最少问题
题目描述:
输入两个整数n(0<n<100001)和k(0<k<100001),通过对n连续进行加1或减1或乘以2这3种操作,使得n最后结果正好等于k(同一种操作可以使用多次也可以不使用),要求最后输出最少的操作次数。
例如:n为5,k为17,通过减1、乘以2、乘以2、加1四次操作得到17,也就是5-1=4,42=8、82=16,16+1=17.
输入描述
输入两个整数n和k(n和k之间以一个空格隔开)
输出描述
输出最少的操作次数
样例输入
5 17
样例输出
4
答案:
参考代码一:
#include <cstdio>
#include <iostream>
#include <queue>
using namespace std;
struct node {
int pos, step;
};
int v[100005];
queue<node> q;
int main() {
int n, k;
cin >> n >> k;
v[n] = 1;
q.push((node){n, 0});
while (!q.empty()) {
node t = q.front();
q.pop();
// cout<<t.pos<<" "<<t.step<<endl;
if (t.pos == k) {
cout << t.step << endl;
break;
}
if (t.pos + 1 < 100005 && v[t.pos + 1] == 0) {
v[t.pos + 1] = 1;
q.push((node){t.pos + 1, t.step + 1});
}
if (t.pos - 1 >= 0 && v[t.pos - 1] == 0) {
v[t.pos - 1] = 1;
q.push((node){t.pos - 1, t.step + 1});
}
if (t.pos * 2 < 100005 && v[t.pos * 2] == 0) {
v[t.pos * 2] = 1;
q.push((node){t.pos * 2, t.step + 1});
}
}
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 8;
int ans[N], n, k;
queue<int> q;
void bfs() {
ans[n] = 0;
q.push(n);
while (!q.empty()) {
int x = q.front();
q.pop();
if (x * 2 < N && ans[x * 2] == -1) {
ans[x * 2] = ans[x] + 1;
q.push(x * 2);
}
if (x + 1 < N && ans[x + 1] == -1) {
ans[x + 1] = ans[x] + 1;
q.push(x + 1);
}
if (x - 1 > 0 && ans[x - 1] == -1) {
ans[x - 1] = ans[x] + 1;
q.push(x - 1);
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> k;
memset(ans, -1, sizeof(ans));
bfs();
cout << ans[k] << '\n';
return 0;
}
评分标准:
20分:能正确输出一组数据;
20分:能正确输出两组数据;
20分:能正确输出三组数据。
第11题:回形取数
提示信息:
回形取数是沿着一个数字矩阵的左上角向下开始移动取数当前方没有数字或者数字已经被取过就会左转继续移动取数当没有数可取时回形取数结束,如下图所示
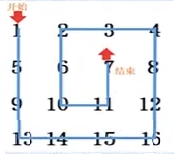
回形取数结束后会产生一条线路图,也就是数字线路。
上路为:1,5,9,13,14,15,16,12,8,4,3,2,6,10,11,7
题目描述:
用户分行输入两个正整数(2<=正整数<=20),第一个数代表数字矩阵的行数,第二个数代表数字矩阵的列数,数字矩阵的数字为从1开始的正整数,根据回形取数规则将最终的数字线路输出(数字线路中的每个数字之间需要有一个英文逗号隔开)。
例如:
输入的是2和3数字矩阵为:
1 2 3
4 5 6
数字线路为:1,4,5,6,3,2
输入的是4和3数字矩阵为:
1 2 3
4 5 6
7 8 9
10 11 12
数字线路为:1,4,7,10,11,12,9,6,3,2,5,8
注:数字矩阵不需要输入此处只为展示
输入描述
第一行输入一个正整数作为行数
第二行输入一个正整数作为列数
编出描述
根据回形取数规则将数字线路输出(数字线路中的每数字之间需要有一个英文逗号隔开)
样例输入
3
2
样例输出
1,3,5,6,4,2
答案:
参考代码一:
#include <cstdio>
#include <iostream>
using namespace std;
int v[105][105], a[105][105];
int main() {
int n, m, k = 0;
int i, j;
cin >> n >> m;
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
a[i][j] = ++k;
i = k = 1;
j = 0;
cout << a[0][0];
v[0][0] = 1;
while (k < n * m) {
while (i < n && v[i][j] == 0) {
cout << "," << a[i][j];
v[i][j] = 1;
i++;
k++;
}
i--;
j++;
while (j < m && v[i][j] == 0) {
cout << "," << a[i][j];
v[i][j] = 1;
j++;
k++;
}
i--;
j--;
while (i >= 0 && v[i][j] == 0) {
cout << "," << a[i][j];
v[i][j] = 1;
i--;
k++;
}
i++;
j--;
while (j >= 0 && v[i][j] == 0) {
cout << "," << a[i][j];
v[i][j] = 1;
j--;
k++;
}
i++;
j++;
}
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
const int N = 28;
const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};
int n, m, a[N][N], cnt;
vector<int> ans;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
a[i][j] = ++cnt;
int x = 1, y = 1, k = 0;
while (cnt) {
ans.push_back(a[x][y]);
a[x][y] = 0;
--cnt;
if (a[x + dx[k]][y + dy[k]])
x += dx[k], y += dy[k];
else
k = (k + 1) & 3, x += dx[k], y += dy[k];
}
for (unsigned i = 0; i < ans.size(); ++i) {
if (i == ans.size() - 1)
cout << ans[i] << '\n';
else
cout << ans[i] << ',';
}
return 0;
}
评分标准:
20分:能正确输出一组数据;
20分:能正确输出两组数据;
20分:能正确输出三组数据。
第12题:带分数
提示信息:
带分数是分数的一种形式,带分数包含两个部分:整数部分和真分数部分.
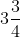
例如:
5用带分数形式可表示为:3+2956/1478,3+2956/1478,3+9562/4781,3+9712/4856
要求:带分数中,数字1-9分别出现且只出现一次。
5的带分数形式有4种表示法.
输出这个正整数满足要求的带分数表示方法,一共有多少种
样例输入
100
样例输出
11
答案:
参考代码一:
// 带分数(暴力枚举)
#include <algorithm>
#include <cstdio>
#include <iostream>
using namespace std;
int n, cnt = 0;
int p[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
bool check(int x, int y) {
int a, b, c;
a = b = c = 0;
for (int i = 0; i < x; i++)
a = a * 10 + p[i];
for (int i = x; i < y; i++)
b = b * 10 + p[i];
for (int i = y; i < 9; i++)
c = c * 10 + p[i];
if (b % c == 0 && a + b / c == n)
return true;
else
return false;
}
int main() {
cin >> n;
do {
for (int i = 1; i < 7; i++)
for (int j = i + 1; j < 8; j++)
if (check(i, j))
cnt++;
} while (next_permutation(p, p + 9));
cout << cnt << endl;
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n, a[18], sum[18], pw[18], ans;
inline ll num(int st, int ed) {
return sum[ed] - pw[ed - st + 1] * sum[st - 1];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
pw[0] = 1;
for (int i = 1; i <= 9; ++i)
a[i] = i, pw[i] = pw[i - 1] * 10;
do {
for (int i = 1; i <= 9; ++i)
sum[i] = sum[i - 1] * 10 + a[i];
for (int i = 1; i <= 8; ++i) {
ll zs = sum[i];
for (int j = i + 1; j <= 8; ++j) {
ll fz = num(i + 1, j), fm = num(j + 1, 9);
if (fz % fm == 0 && zs + fz / fm == n)
++ans;
}
}
} while (next_permutation(a + 1, a + 10));
cout << ans << '\n';
return 0;
}
评分标准:
20分:能正确输出一组数据;
20分:能正确输出两组数据;
20分:能正确输出三组数据。









![[UE 虚幻引擎] DTLoadFbx 运行时加载FBX本地模型插件说明](https://img-blog.csdnimg.cn/img_convert/410c80587167f9947ed05ae55bbe5912.png)