一个月速刷leetcodeHOT100 day15 彻底搞懂回溯算法以及相关题目

回溯算法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案

全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

**输入：**nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

**输入：**nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

**输入：**nums = [1]
输出：[[1]]

const permute = (nums) => {
// 1. 设置结果集

const result = [];

// 2. 回溯

const recursion = (path, set) => {

// 2.1 设置回溯终止条件

if (path.length === nums.length) {

// 2.1.1 推入结果集

result.push(path.concat());

// 2.1.2 终止递归

return;

}

// 2.2 遍历数组

for (let i = 0; i < nums.length; i++) {

// 2.2.1 必须是不存在 set 中的坐标

if (!set.has(i)) {

// 2.2.2 本地递归条件（用完记得删除）

path.push(nums[i]);

set.add(i);

// 2.2.3 进一步递归

recursion(path, set);

// 2.2.4 回溯：撤回 2.2.2 的操作

path.pop();

set.delete(i);

}

}

};

recursion([], new Set());

// 3. 返回结果

return result;

};

子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的
子集
（幂集）。
解集不能包含重复的子集。你可以按 任意顺序 返回解集。
示例 1：
**输入：**nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

**输入：**nums = [0]
输出：[[],[0]]

var letterCombinations = (digits) => {

if (digits.length == 0) return [];

const res = [];

const map = {//建立电话号码和字母的映射关系

2: "abc",

3: "def",

4: "ghi",

5: "jkl",

6: "mno",

7: "pqrs",

8: "tuv",

9: "wxyz",

};

  

const dfs = (curStr, i) => {//curStr是递归每一层的字符串，i是扫描的指针

if (i > digits.length - 1) {//边界条件，递归的出口

res.push(curStr); //其中一个分支的解推入res

return; //结束递归分支，进入另一个分支

}

const letters = map[digits[i]]; //取出数字对应的字母

for (const l of letters) {

//进入不同字母的分支

dfs(curStr + l, i + 1); //参数传入新的字符串，i右移，继续递归

}

};

dfs("", 0); // 递归入口，传入空字符串，i初始为0的位置

return res;

};

数组总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

**输入：**candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

var combinationSum = function(candidates, target) {

// 先队候选数字排序

candidates = candidates.sort((a,b)=>a-b);

const result = []; // 存储最后返回的结果

const path = []; // 路径

// sum 为当前路径上的所有元素之和

function backTrack(startIndex,sum) {

// 判断 和 是否与target相等

if( sum === target) {

result.push([...path]);

}

for(let i = startIndex; i < candidates.length; i++){

// 剪枝

if(candidates[i]+sum > target) return;

path.push(candidates[i]);

// candidates[i]表示候选数组中第i个元素的值

backTrack(i, sum + candidates[i]);

path.pop();

}

}

backTrack(0 , 0);

return result;

};

括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

**输入：**n = 3
输出：[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]

示例 2：

**输入：**n = 1
输出：[“()”]

var generateParenthesis = function(n) {

const res = []; // 输出的结果数组

const generate = (str, left, right) => {

if (str.length == 2 * n) { // 字符串构建完成

res.push(str); // 将字符串加入res

return; // 结束当前递归（结束当前搜索分支）

}

if (left > 0) { // 只要左括号有剩，可以选它，继续递归做选择

generate(str + '(', left - 1, right);

}

if (right > left) { // 右括号的保有数量大于左括号的保有数量，才能选右括号

generate(str + ')', left, right - 1);

}

};
  
generate('', n, n); // 递归的入口，初始字符串是空字符串，初始括号数量都是n

return res;


};

单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

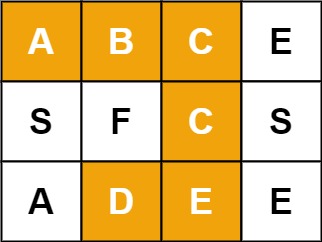
**输入：**board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
**输出：**true

示例 2：

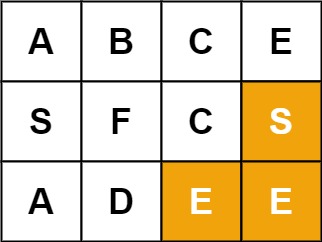
**输入：**board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “SEE”
**输出：**true

示例 3：

**输入：**board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB”
**输出：**false

var exist = function (board, word) {

let m = board.length;

let n = board[0].length;

//越界处理

// board[-1] = []; // 这里处理比较比较巧妙，利用了js的特性

// board.push([]);

  

//寻找首个字母

for (let x = 0; x < m; x++) {

for (let y = 0; y < n; y++) {

if (word[0] === board[x][y]) {

if (dfs(word, board, x, y, 0)) {

return true;

}

}

}

}

return false;

};

let dfs = function (word, board, x, y, index) {

let m = board.length;

let n = board[0].length;

if (index + 1 === word.length) return true;

  

var tmp = board[x][y];

// 标记该元素已使用

board[x][y] = false

if (y+1 < n && board[x][y + 1] === word[index + 1] && dfs(word, board, x, y + 1, index + 1)) return true;

if (y - 1 >= 0 && board[x][y - 1] === word[index + 1] && dfs(word, board, x, y - 1, index + 1)) return true;

if (x + 1 < m && board[x + 1][y] === word[index + 1] && dfs(word, board, x + 1, y, index + 1)) return true;

if (x - 1 >= 0 && board[x - 1][y] === word[index + 1] && dfs(word, board, x - 1, y, index + 1)) return true;

// 回溯

board[x][y] = tmp;

}

分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是

回文串

。返回 s 所有可能的分割方案。

示例 1：

**输入：**s = “aab”
输出：[[“a”,“a”,“b”],[“aa”,“b”]]

示例 2：

**输入：**s = “a”
输出：[[“a”]]

var partition = function(s) {
    //判断回文
    const isPal = function(s, l ,r) {
        while(l < r) {
            if(s[l] !== s[r]) {
                return false;
            }
            l++;
            r--;
        }
        return true;
    }
    let res = [];
    let path = [];
    const bt = function(startIndex) {
        //如果已经切割到最后就结束
        if(startIndex === s.length) {
            res.push([...path]);
            return;
        } 
        for(let i = startIndex; i < s.length; i++) {
            // 是回文子串
            if(isPal(s, startIndex, i)) {
                path.push(s.slice(startIndex, i + 1));  //slice是右开，所以得加1
                bt(i + 1);  
                path.pop(); //回溯
            } else {
                continue;
            }
        }
    }
    bt(0);
    return res;
};