PCA最常见的应用之一就是将高维数据集可视化。一般对于有两个以上特征的数据,很难绘制散点图,。对于Iris(鸢尾花)数据集,我们可以创建散点矩阵图,通过展示特征所有可能的两两组合来展示数据的局部图像。
不过类似cancer数据集,包含30个特征,这就导致需要绘制30*14=420张散点图。
不过还可以用一种简单的可视化方法——对每个特征分别计算两个类别的直方图:
import mglearn.plots
import numpy as np
from sklearn.datasets import make_blobs,load_breast_cancer
import matplotlib.pyplot as plt
cancer=load_breast_cancer()
fig,axes=plt.subplots(15,2,figsize=(10,20))
malignant=cancer.data[cancer.target==0]
benign=cancer.data[cancer.target==1]
ax=axes.ravel()
for i in range(30):
_,bins=np.histogram(cancer.data[:,i],bins=50)
ax[i].hist(malignant[:,i],bins=bins,color=mglearn.cm3(0),alpha=0.5)
ax[i].hist(benign[:,i],bins=bins,color=mglearn.cm3(2),alpha=0.5)
ax[i].set_title(cancer.feature_names[i])
ax[i].set_yticks(())
ax[0].set_xlabel('Feature magnitude')
ax[0].set_ylabel('Frequency')
ax[0].legend(['malignant','benign'],loc='best')
fig.tight_layout()
plt.show()

这里为每个特征创建了一个直方图,计算具有某一特征的数据点在特点范围内(bin)的出现频率。
每张图都包含两个直方图,一个是良性类别的所有点(蓝色),一个是恶性类别的所有点(红色)。这样可以了解每个特征在两个类别中的分布情况,也可以猜测哪个特征能够很好的区分良性样本和恶性样本。
但是,这种图无法展示变量之间的相互作用以及这种相互作用与类别之间的关系。利用PCA,我们可以获取到主要的作用,并得到稍微完整的图像。我们可以找到前两个主成分,并在这个新的二维空间中用散点图将数据可视化:
cancer=load_breast_cancer()
scaler=StandardScaler()
scaler.fit(cancer.data)
X_scaler=scaler.transform(cancer.data)
将PCA对象实例化,调用fit方法找到主成分,然后调用transform来旋转并降维。默认情况下,PCA仅旋转并移动数据,但保留所有的主成分。为了降低数据的维度,我们需要在创建PCA对象时指定想要保留的主成分个数。
pca=PCA(n_components=2)
pca.fit(X_scaler)
X_pca=pca.transform(X_scaler)
print('Original shape:{}'.format(str(X_scaler.shape)))
print('Reduced shape:{}'.format(str(X_pca.shape)))

现在对前两个主成分作图:
plt.figure(figsize=(8,8))
mglearn.discrete_scatter(X_pca[:,0],X_pca[:,1],cancer.target)
plt.legend(cancer.target_names,loc='best')
plt.gca().set_aspect('equal')
plt.xlabel('first')
plt.ylabel('second')
plt.show()
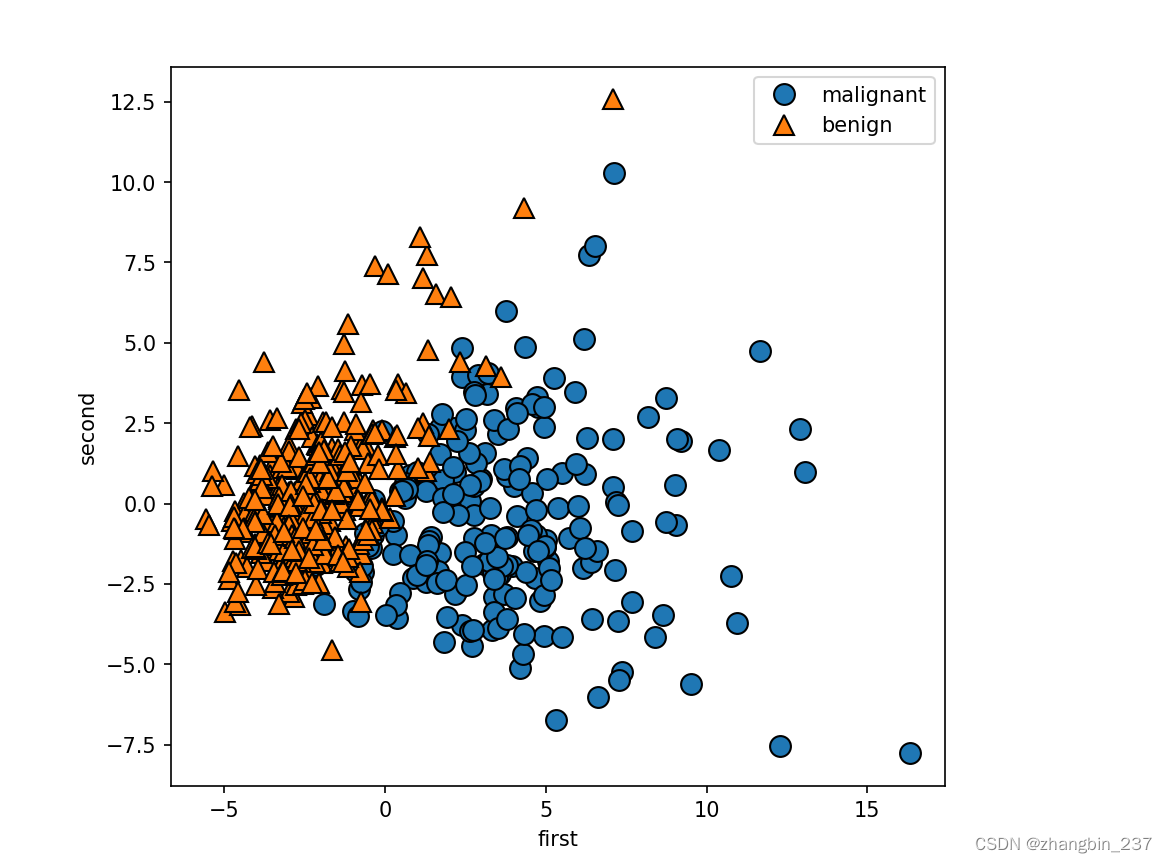
需要注意的是,PCA是一种无监督方法,在寻找旋转方向时没有用到任何类别信息。它只是观察数据中的相关性。
对于这里的散点图,我们绘制了第一主成分和第二主成分的关系,然后利用类别信息对数据点进行着色。在这个二维空间中的两个类别被很好的分离。这让我们相信,即使是线性分类器也可以在区分这个两个类别时表现的相当不错。
PCA的一个缺点是:通常不容易对图中的两个轴进行解释。主成分对应于原始数据中的方向,所以它们是原始特征的拟合。但这些组合往往非常复杂,这一点我们很快就会看到。
在拟合过程中,主成分被保存在PCA对象的components_属性中:
print('PCA components shape:{}'.format(pca.components_.shape))![]()
components_中的每一行对应一个主成分,它们按重要性排序。列对应于PCA的原始特征属性,components_的内容:
print('PCA components:{}'.format(pca.components_))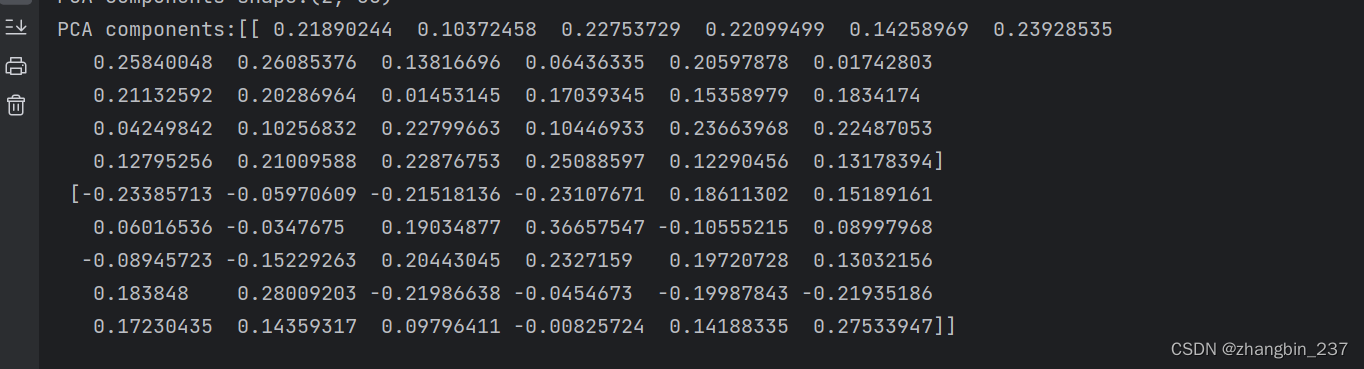
还可以用热图将系数可视化,这可能更容易理解:
plt.matshow(pca.components_,cmap='viridis')
plt.yticks([0,1],['first','second'])
plt.colorbar()
plt.xticks(range(len(cancer.feature_names)),
cancer.feature_names,rotation=60,ha='left')
plt.xlabel('feature')
plt.ylabel('Principal components')
plt.show()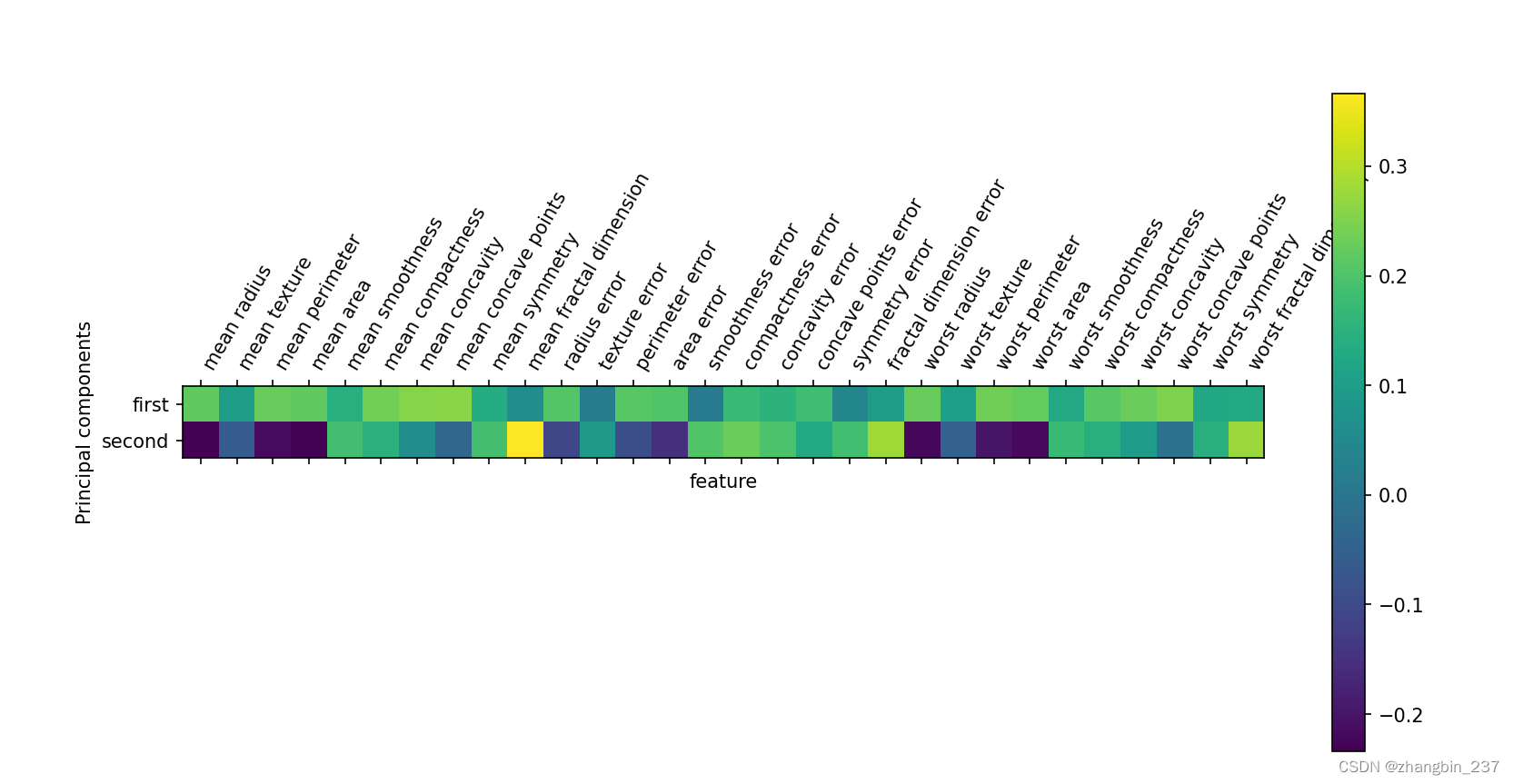
可以看到,在第一个主成分中,所有特征的符号相同(均为正)。这意味着在所有特征之间存在普遍的相关性,如果一个测量值很大的话,其他的测量值可能也较大。第二个主成分的符号有正有负,而且两个主成分都包含所有30个特征。这种所有特征的混合使得解释上图中的坐标轴非常困难。
![[论文笔记]AIOS: LLM Agent Operating System](https://img-blog.csdnimg.cn/img_convert/24e42f09787b649fcdd18b52f19a24f1.png)