码蹄集部分题目（2024OJ赛18期；并查集+ST表+贪心）

news2024/11/18 7:48:57

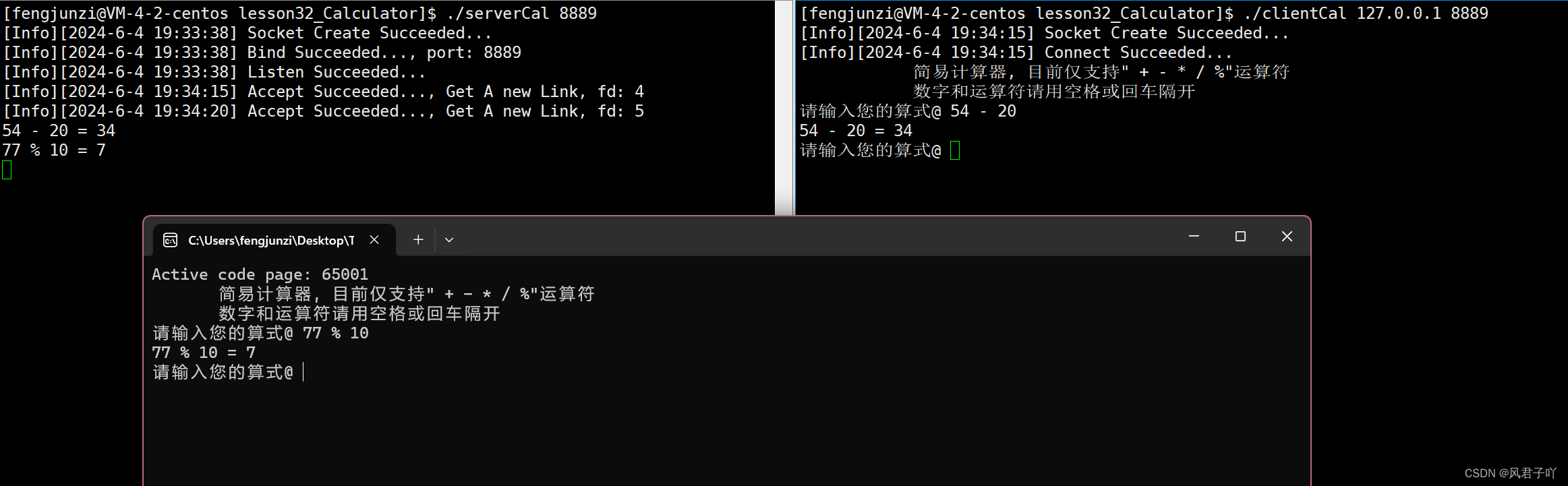
1🐋🐋史莱姆融合（钻石；并查集）

时间限制：1秒

占用内存：128M

🐟题目描述

🐟题目思路

这道题目使用并查集，同一集合的所有元素的最顶上的祖父节点是统一的。这里记录每个集合的最左端元素（最顶上的祖父节点）和最右端元素，便于集合更新。

MT3052 史莱姆融合_哔哩哔哩_bilibili

🐟代码

#include<bits/stdc++.h> 
​
using namespace std;
const int N=1e6+5;
int n,fa[N],so[N],nxt[N];//集合最左端fa，集合最右端so，下一个元素nxt
​
int find(int x) {return x==fa[x]?x:(fa[x]=find(fa[x]));}//找集合最左端元素
​
void merge(int i,int j)//集合合并
{
    int x=find(i),y=find(j);//两个集合的最左端
    if(x!=y)
    {
        nxt[so[x]]=y;//第一个集合的最右端的下一个元素就是第二个集合的最左端元素
        fa[y]=x;//更新最左端
        so[x]=so[y];//更新最右端
    }
}
​
int main( )
{
    int x,y;
    cin>>n;
    for(int i=1;i<=n;i++) fa[i]=so[i]=i;
    for(int i=0;i<n-1;i++)
    {
        cin>>x>>y;
        merge(x,y);
    }
    for(int i=find(1);i;i=nxt[i]) cout<<i<<" ";
    return 0;
}

2🐋🐋区间最小值（钻石；ST表）

时间限制：1秒

占用内存：128M

🐟题目描述

🐟题目思路

ST表用于解决区间最值问题，基于分治和倍增思想。

  • ST表中定义了一个二维数组mn[N] [M]，mn[i] [j]表示区间[i, i + 2^j + 1]内的最大值

  • 根据倍增思想，给出状态转移方程mn[i] [j] = max(mn[i] [j - 1], mn[i + 2^j - 1^] [j - 1])

ST表详解推荐：ST表详解-CSDN博客

🐟代码

#include<bits/stdc++.h> 
​
using namespace std;
const int N=1e5+5;
int m,n,a[N],mn[N][50],Lg[N],ans;
​
void pre()
{
    Lg[1]=0;
    for(int i=2;i<=n;i++) Lg[i]=Lg[i>>1]+1;//求对数，得到每段的区间结束位置
}
​
void ST_create()
{
    for(int i=1;i<=n;i++) mn[i][0]=a[i];//mn[i][j]，当j为0时，区间长度2^j为0，则区间最大值就是区间的唯一元素a[i]
    for(int j=1;j<=Lg[n];j++)//之前已经计算过区间长度为0的情况，这里区间长度由2^1 到 2^Lg[n] 
    {
        for(int i=1;i<=n-(1<<j)+1;i++)//确定区间左端点，区间范围为[i, i + 2^j - 1],所以 i + 2^j - 1 <= n
        {
            mn[i][j]=min(mn[i][j-1],mn[i+(1<<(j-1))][j-1]);//状态转移方程
        }
    }
}
​
int ST_query(int l,int r)//区间查询
{
    int k=Lg[r-l+1];
    return min(mn[l][k],mn[r-(1<<k)+1][k]);
}
​
int main( )
{
    int a1,a2;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    pre();
    ST_create();
    while(m--)
    {
        cin>>a1>>a2;
        cout<<ST_query(a1,a2)<<endl;
    }
    return 0;
}

3🐋🐋区间gcd（钻石；ST表）

时间限制：1秒

占用内存：64M

🐟题目描述

🐟题目思路

这道题目也是使用ST表，pre、create和query除了将min改成gcd没有变化，gcd使用递归的方式求取。

MT3051 区间gcd_哔哩哔哩_bilibili

🐟代码

用时少：

#include<bits/stdc++.h> 
​
using namespace std;
const int N=2e5+5;
int m,n,a[N],mn[N][50],Lg[N],ans;
​
int read()
{
    int ans=0;
    char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9')
    {
        ans=ans*10+ch-'0';
        ch=getchar();
    }
    return ans;
}
​
void write(int x)
{
    if(x>=10) write(x/10);
    putchar(x%10+'0');
}
​
int gcd(int a,int b){return b==0?a:gcd(b,a%b);}
​
void pre()
{
    Lg[1]=0;
    for(int i=2;i<=n;i++) Lg[i]=Lg[i>>1]+1;//求对数，得到每段的区间结束位置
}
​
void ST_create()
{
    for(int i=1;i<=n;i++) mn[i][0]=a[i];//mn[i][j]，当j为0时，区间长度2^j为0，则区间最大值就是区间的唯一元素a[i]
    for(int j=1;j<=Lg[n];j++)//之前已经计算过区间长度为0的情况，这里区间长度由2^1 到 2^Lg[n] 
    {
        for(int i=1;i<=n-(1<<j)+1;i++)//确定区间左端点，区间范围为[i, i + 2^j - 1],所以 i + 2^j - 1 <= n
        {
            mn[i][j]=gcd(mn[i][j-1],mn[i+(1<<(j-1))][j-1]);//状态转移方程
        }
    }
}
​
int ST_query(int l,int r)//区间查询
{
    int k=Lg[r-l+1];
    return gcd(mn[l][k],mn[r-(1<<k)+1][k]);
}
​
int main( )
{
    int a1,a2;
    n=read();
    m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    pre();
    ST_create();
    while(m--)
    {
        a1=read();
        a2=read();
        ans=ST_query(a1,a2);
        write(ans);
        putchar('\n');
    }
    return 0;
}

占内存少：

摘自——小码_63705

#include<bits/stdc++.h> 
​
using namespace std;
const int N=3e5+5;
​
int gcd(int a,int b)
{
    if(!b) return a;
    else return gcd(b,a%b);
}
​
int dp[N][20],a[N],len[N];
​
int query(int l,int r)
{
    int k=len[r-l+1];
    return gcd(dp[l][k],dp[r-(1<<k)+1][k]);
}
​
inline int read()
{
    char c=getchar();
    int x=0,f=1;
    while(c<'0'||c>'9')
    {
        if(c=='-') f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        x=x*10+c-'0';
        c=getchar();
    }
    return x*f;
}
​
int main( )
{
    len[0]=1;
    for(int i=2;i<N-2;i++) len[i]=len[i/2]+1;
    int n;
    n=read();
    int ncase;
    ncase=read();
    for(int i=1;i<=n;i++) 
    {
        *(a+i)=read();
        dp[i][0]=a[i];
    }
    for(int j=1;j<=len[n];j++)
    {
        for(int i=1;i<=n;i++)
        {
            dp[i][j]=gcd(dp[i][j-1],dp[i+(1<<j-1)][j-1]);
        }
    }
    while(ncase--)
    {
        int l=read(),r=read();
        printf("%d\n",query(l,r));
    }
    return 0;
}

4🐋🐋检测敌人（钻石；贪心）

时间限制：1秒

占用内存：128M

🐟题目描述

🐟题目思路

贪心思路：一个设备检测尽可能多的敌人。

不同于用设备找敌人，这道题目需要用敌人找设备，以敌人为圆心画圈，找到可用检测到我的x轴上的所有范围，那么在这个范围内放设备都可以检测到我。

贪心的实现就是通过对比两个区间是否有重叠，得知可否共用设备。

【码蹄集进阶塔全题解08】算法基础：贪心 MT2080 – MT2092_哔哩哔哩_bilibili

🐟代码

#include<bits/stdc++.h> 
​
using namespace std;
const int N=1005;
struct node
{
    double x,y,l,r;
    bool v;
}e[N];
​
bool cmp(node a,node b)
{
    return a.r<b.r;
}
​
int main( )
{
    int n;
    double r;
    while(cin>>n>>r&&!(n==0&&r==0))
    {
        bool flag=false;
        memset(e,0,sizeof(e));
        for(int i=1;i<=n;i++)
        {
            cin>>e[i].x>>e[i].y;
            if(r*r<e[i].y*e[i].y) flag=true;//以每个敌人为圆心画圆，圆圈范围内的仪器能检测到敌人
            else//计算能检测到敌人的x轴坐标范围
            {
                e[i].l=-sqrt(r*r-e[i].y*e[i].y)+e[i].x;
                e[i].r=sqrt(r*r-e[i].y*e[i].y)+e[i].x;
                e[i].v=false;
            }
        }
        if(flag)
        {
            cout<<-1<<endl;
            continue;
        }
        sort(e+1,e+1+n,cmp);
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            if(e[i].v==false)//表示这个敌人还没能被检测到
            {
                for(int j=i;j<=n;j++)
                {
                    if(e[j].v==false&&e[j].l<=e[i].r&&e[j].r>=e[i].r) e[j].v=true;//我们有重叠区域，用一个设备就行了
                }
                e[i].v=true;
                ans++;//所需设备数加一
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

5🐋🐋小码哥的福利（钻石；贪心）

时间限制：1秒

占用内存：128M

🐟题目描述

🐟题目思路

贪心思路：每次分甜品都要尽可能地达到平均值。

这道题目的思路就是，将所有手下按耐受度排序，将所有甜品按甜度排序；找到能吃掉这个甜品的手下，让他全部吃掉；然后对所有手下吃掉的甜品数量进行分配。根据耐受度限制，甜品只能往右分，也就是往耐受度高的手下那里分，那么每次都计算出来从我到最后一个手下我们吃的甜品数量的平均值，然后如果我吃的比这个平均值多，就把多的甜品分给下一个人，以此类推我从头遍历到尾。

【码蹄集进阶塔全题解08】算法基础：贪心 MT2080 – MT2092_哔哩哔哩_bilibili

🐟代码

#include<bits/stdc++.h> 
​
using namespace std;
#define ll long long
const int N=55;
ll n,m,a[N],sum[N],ans;
struct node
{
    ll b,c;
}sweet[N];
​
int cmp(node a,node b){return a.b<b.b;}
​
ll add(int l,int r)
{
    ll ans=0;
    for(int i=l;i<=r;i++) ans+=sum[i];
    return ans;
}
​
int main( )
{
    cin>>n;
    ll maxm=0;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        maxm=max(maxm,a[i]);
    }
    sort(a+1,a+1+n);
    cin>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>sweet[i].b;
        if(sweet[i].b>maxm)//甜品的甜度超过手下的最大甜品耐受度了，无法吃完
        {
            cout<<-1<<endl;
            return 0;
        }
    }
    for(int i=1;i<=m;i++) cin>>sweet[i].c;
    sort(sweet+1,sweet+1+m,cmp);//按照甜度大小排列
    for(int i=1;i<=m;i++)//遍历所有甜品i
    {
        for(int j=1;j<=n;j++)//遍历所有手下j
        {
            if(sweet[i].b<=a[j])
            {
                sum[j]+=sweet[i].c;//手下j吃掉甜度为i的所有甜品
                break;
            }
        }
    }
    //平均化吃掉的数量
    //甜品转移只能向右转移，也就是转移给耐受度更高的手下
    for(int i=1;i<=n;i++)//遍历所有手下
    {
        ll tmp=(add(i,n))/(n-i+1);//将往右的这些所有吃的甜品数量平均
        if(tmp<=sum[i])//这个人吃多了，分走甜品
        {
            sum[i+1]+=sum[i]-tmp;
            sum[i]=tmp;
        }
    }
    for(int i=1;i<=n;i++) ans=max(ans,sum[i]);//找出最大sum
    cout<<ans<<endl;
    return 0;
}

6🐋🐋屠龙勇者（黄金；贪心）

时间限制：1秒

占用内存：128M

🐟题目描述

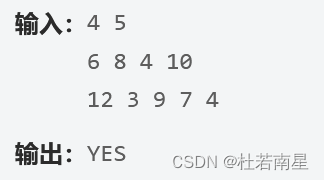
🐟题目思路

贪心思想：用最强的勇士砍最大的头。

那么就是将d和w数组分别排序，最多有m-n个spare的勇士可以用来砍这个头，所以对i来说最强的勇士就是第i+m-n个勇士，如果这个最强的勇士都没法砍这个头，那么就失败了。同样的贪心思想，这些spare的勇士也是能力值低的那些。

🐟代码

#include<bits/stdc++.h> 
​
using namespace std;
const int N=1e5+5;
int d[N],w[N],n,m;
int main( )
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>d[i];
    for(int i=1;i<=m;i++) cin>>w[i];
    sort(d+1,d+1+n);
    sort(w+1,w+1+m);
    if(n>m)
    {
        cout<<"NO";
        return 0;
    }
    for(int i=n;i>=1;i--)
    {
        if(w[i+m-n]<d[i])//最多有m-n个spare的勇士
        {
            cout<<"NO";
            return 0;
        }
    }
    cout<<"YES";
    return 0;
}

有问题我们随时评论区见~

⭐点赞收藏不迷路~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1799597.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[NOVATEK] NT96580行车记录仪功能学习笔记

[NOVATEK] NT96580行车记录仪功能学习笔记

一、u-Boot升级灯 运行u-Boot程序时LED灯闪烁，找到运行过程中一直在运行的函数在里面进行LED引脚电平的翻转 宏定义 Z:\SunFan\AHD580\pip\na51055_PIP\BSP\u-boot\include\configs\nvt-na51055-evb.h Z:\SunFan\AHD580\pip\na51055_PIP\BSP\u-boot\drivers\mtd\nvt_flash_…
阅读更多...
【BOM02】本地存储

【BOM02】本地存储

一&#xff1a;什么是本地存储 数据存储在用户浏览器中&#xff0c;用户设置、读取方便&#xff0c;同时页面刷新时不会丢失数据。存储在浏览器中数据约5M&#xff0c;分为sessionStorage和localStorage两种存储方式 二&#xff1a;localStorage存储 作用 将数据永久存储在…
阅读更多...
idm2024最新完美破解版免费下载 idm绿色直装版注册机免费分享 idm永久激活码工具

idm2024最新完美破解版免费下载 idm绿色直装版注册机免费分享 idm永久激活码工具

IDM 2024破解版重新开发了调度程序和MMS协议支持、重新设计和增强的下载引擎、与所有最新浏览器的独特高级集成、改进的工具栏以及大量其他改进和新功能&#xff0c;这一全新的更新&#xff0c;使得IDM下载器更加完美。值得一提的是&#xff0c;它可以借助油猴浏览器的脚本&…
阅读更多...
linux系统——route路由命令

linux系统——route路由命令

route路由对linux内的ip路由表进行操作 计算机间的数据通信是通过网络来实现的&#xff0c;路由就是从源主机到目标主机的转发过程 路由分为静态路由与动态路由&#xff0c;linux中的均为静态路由&#xff0c;动态路由由交换机路由器自动分配规则而来
阅读更多...
2022 hnust 湖科大 javaweb课设 数据库课设 报告+源代码+流程图文件+课设指导书+附赠数据库课堂实验指导书

2022 hnust 湖科大 javaweb课设 数据库课设 报告+源代码+流程图文件+课设指导书+附赠数据库课堂实验指导书

2022 hnust 湖科大 javaweb课设 数据库课设 报告源代码流程图文件课设指导书附赠数据库课堂实验指导书 描述 湖南科技大学大二下学期先后开展java web和数据库课程设计&#xff0c;两个课设项目可以通用&#xff0c;老师一般会允许自拟选题&#xff0c;所以在此统一打包&…
阅读更多...
关于使用南墙waf防护halo网站主页请求404报错的解决方案

关于使用南墙waf防护halo网站主页请求404报错的解决方案

文章目录 环境说明问题展示原因探究解决方法 环境说明 在1panel应用商店&#xff0c;部署南墙waf(docker版)halo(2.16.1社区版)注意部署过程中注意uuwaf必须勾选允许外部访问&#xff0c;halo可以不勾选[这里为了证明确实是南墙waf的原因&#xff0c;选择勾选] 问题展示 使…
阅读更多...
css实现文字打字机效果

css实现文字打字机效果

html <body><p class"line animation">我和我的祖国&#xff0c;一刻也不能分割</p> </body>css <style type"text/css">html,body {height: 100%;}body {overflow: hidden;display: flex;justify-content: center;align-i…
阅读更多...
D3D 顶点格式学习

D3D 顶点格式学习

之前D3D画三角形的代码中有这一句&#xff0c; device.VertexFormat CustomVertex.TransformedColored.Format; 这是设置顶点格式&#xff1b; 画出的三角形如下&#xff0c; 顶点格式是描述一个三维模型的顶点信息的格式&#xff1b;可以包含以下内容&#xff0c; 位置…
阅读更多...
算法：前缀和题目练习

算法：前缀和题目练习

目录 题目一&#xff1a;一维前缀和[模版] 题目二&#xff1a;二维前缀和[模版] 题目三&#xff1a;寻找数组的中心下标 题目四&#xff1a;除自身以外数组的乘积 题目五&#xff1a;和为K的子数组 题目六&#xff1a;和可被K整除的子数组 题目七&#xff1a;连续数组 题…
阅读更多...
【工具】Vmware17 安装mac（13.6.7）虚拟机

【工具】Vmware17 安装mac（13.6.7）虚拟机

目录 0.简介 1.环境 2.详细步骤 2.1下载mac镜像&#xff08;可以选择你所需要的&#xff09; 2.2 VMware安装 1&#xff09;创建新的虚拟机 2&#xff09;选择【典型】&#xff0c;点击下一步 3&#xff09;选择【安装程序光盘映像文件】&#xff0c;点击浏览&#xff…
阅读更多...
vue3路由详解，从0开始手动配置路由（vite，vue-router）

vue3路由详解，从0开始手动配置路由（vite，vue-router）

创建一个不含路由的vue项目 &#xff08;查看路由配置可以直接跳过这一段&#xff09; 输入npm指令&#xff0c;然后写一个项目名称&#xff0c;之后一路回车即可 npm create vuelatest 注意这里我们不选引入vue router&#xff0c;成功后可以 查看目录 然后按提示信息输入指…
阅读更多...
如何设置vue3项目中默认的背景为白色

如何设置vue3项目中默认的背景为白色

方法1&#xff1a;通过CSS全局样式 在全局CSS文件中设置&#xff1a; 如果你的项目中有全局的CSS文件&#xff08;如App.vue或专门的CSS文件&#xff09;&#xff0c;你可以直接设置body或html标签的背景颜色。 在src/assets文件夹中&#xff08;或者任何你存放CSS文件的地方&a…
阅读更多...
【机器学习基础】Python编程06：五个实用练习题的解析与总结

【机器学习基础】Python编程06：五个实用练习题的解析与总结

Python是一种广泛使用的高级编程语言，它在机器学习领域中的重要性主要体现在以下几个方面： 简洁易学：Python语法简洁清晰，易于学习，使得初学者能够快速上手机器学习项目。 丰富的库支持：Python拥有大量的机器学习库，如scikit-learn、TensorFlow、Keras和PyTorch等，这些…
阅读更多...
Linux网络-自定义协议、序列化和反序列化、网络计算服务器的实现和Windows端客户端

Linux网络-自定义协议、序列化和反序列化、网络计算服务器的实现和Windows端客户端

文章目录 前言一、自定义协议传结构体对象 序列化和反序列化什么是序列化&#xff1f;反序列化 二、计算器服务端&#xff08;线程池版本&#xff09;1.main.cc2.Socket.hpp3.protocol.hpp4.Calculator.hpp5.serverCal.hpp6.threadPool.hpp7.Task.hpp8. log.hpp 客户端Windows客…
阅读更多...
【回溯算法】N皇后问题·构建多叉决策树，遍历决策节点，做出决策（边），收集答案

【回溯算法】N皇后问题·构建多叉决策树，遍历决策节点，做出决策（边），收集答案

0、前言 在由树形解空间入手&#xff0c;深入分析回溯、动态规划、分治算法的共同点和不同点这篇博客&#xff0c;其实已经对回溯算法的思想、做题框架做出了详细的阐述。这篇文章我们再从N皇后问题&#xff0c;加深我们对其理解。 这里在简单再次对其进行概述&#xff1a; …
阅读更多...
3、前端本地环境搭建

3、前端本地环境搭建

前端本地环境搭建 安装node [node下载地址] https://nodejs.org/en/download/prebuilt-installer 选择LTS的版本进行下载 下载后直接双击点击&#xff0c;选择自己想要安装到的目录一直点下一步即可&#xff08;建议不要安装到c盘&#xff09; 安装完成后配置环境变量&am…
阅读更多...
NLP课程笔记-基于transformers的自然语言处理入门

NLP课程笔记-基于transformers的自然语言处理入门

NLP课程笔记-基于transformers的自然语言处理入门 项目地址2.1 图解attention2.1.1 Seq2seq框架2.1.2 Seq2seq细节2.1.3 Attention1) 基于RNN的seq2seq模型的问题2)基于Attention seq2seq方案 2.2 图解transformer2.2.1 transformer宏观结构单层编码器单层解码器 2.2.2 transfo…
阅读更多...
揭秘FL Studio21.2最新官方免费下载中文破解版！

揭秘FL Studio21.2最新官方免费下载中文破解版！

在音乐创作中&#xff0c;一个优秀的宿主软件是必不可少的。而FL Studio 21.2中文破解汉化免费版&#xff0c;作为一款功能强大、易于上手的宿主软件&#xff0c;已经成为越来越多音乐制作者的首选。那么&#xff0c;它究竟有何魅力呢&#xff1f;下面就让我们一起来了解一下。…
阅读更多...
.Net Core 8.0 IIS部署遇到奇怪的部分接口报404的问题解决

.Net Core 8.0 IIS部署遇到奇怪的部分接口报404的问题解决

本地运行没问题&#xff0c;部署到IIS后&#xff0c;部分接口报404&#xff0c;其它接口都正常。 经和群里讨论&#xff0c;大概意思是接口返回数据比较大的时候&#xff0c;就会出现这个问题。 查看事件查看器&#xff0c;发现应该是数据过大时使用了临时文件夹&#xff0c;…
阅读更多...
CondaSSLError: OpenSSL appears to be unavailable on this machine.

CondaSSLError: OpenSSL appears to be unavailable on this machine.

conda create -n x1 python3.7报错 PS C:\Users\Richardo.M.Song\Desktop\lele_seg\x1> conda create -n x1 python3.7 Collecting package metadata (current_repodata.json): failed CondaSSLError: OpenSSL appears to be unavailable on this machine. OpenSSL is requ…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023