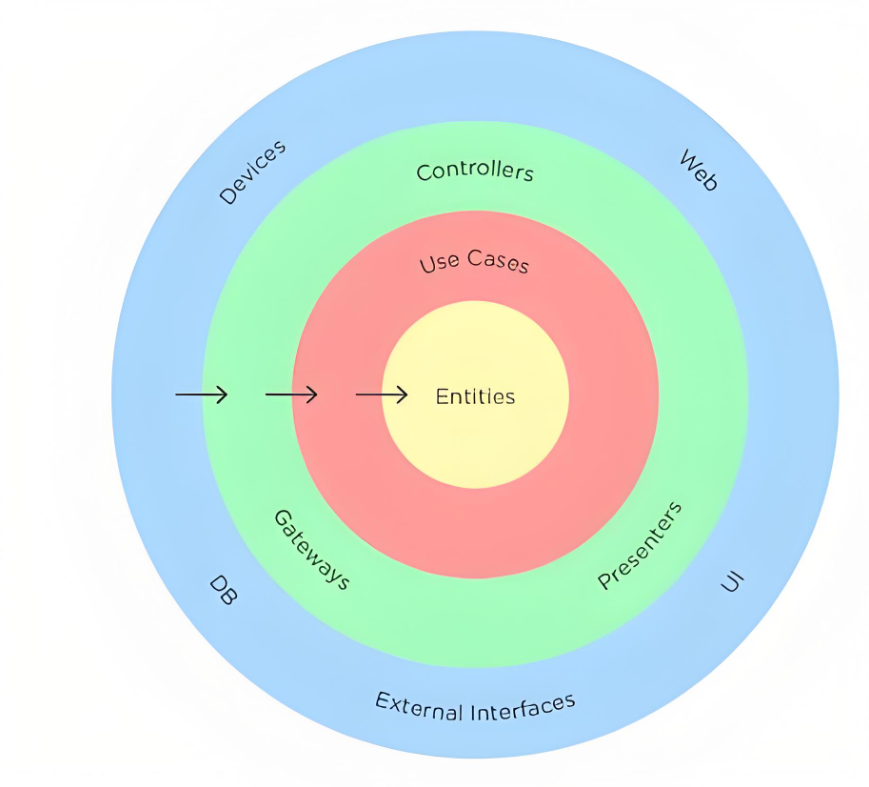
0、前言
在由树形解空间入手,深入分析回溯、动态规划、分治算法的共同点和不同点这篇博客,其实已经对回溯算法的思想、做题框架做出了详细的阐述。这篇文章我们再从N皇后问题,加深我们对其理解。
这里在简单再次对其进行概述:
回溯算法的核心就是构建和遍历一棵【多叉决策树】
- 树的节点是一个决策节点,站在一个节点上我们只需要思考三个问题
- 当前已经做出的选择:路径
- 当前还可以做出哪些选择(选择列表)
- 结束条件:到达叶子决策节点,得到一个答案,进行收集
- 树的边:代表一个决策(选择)
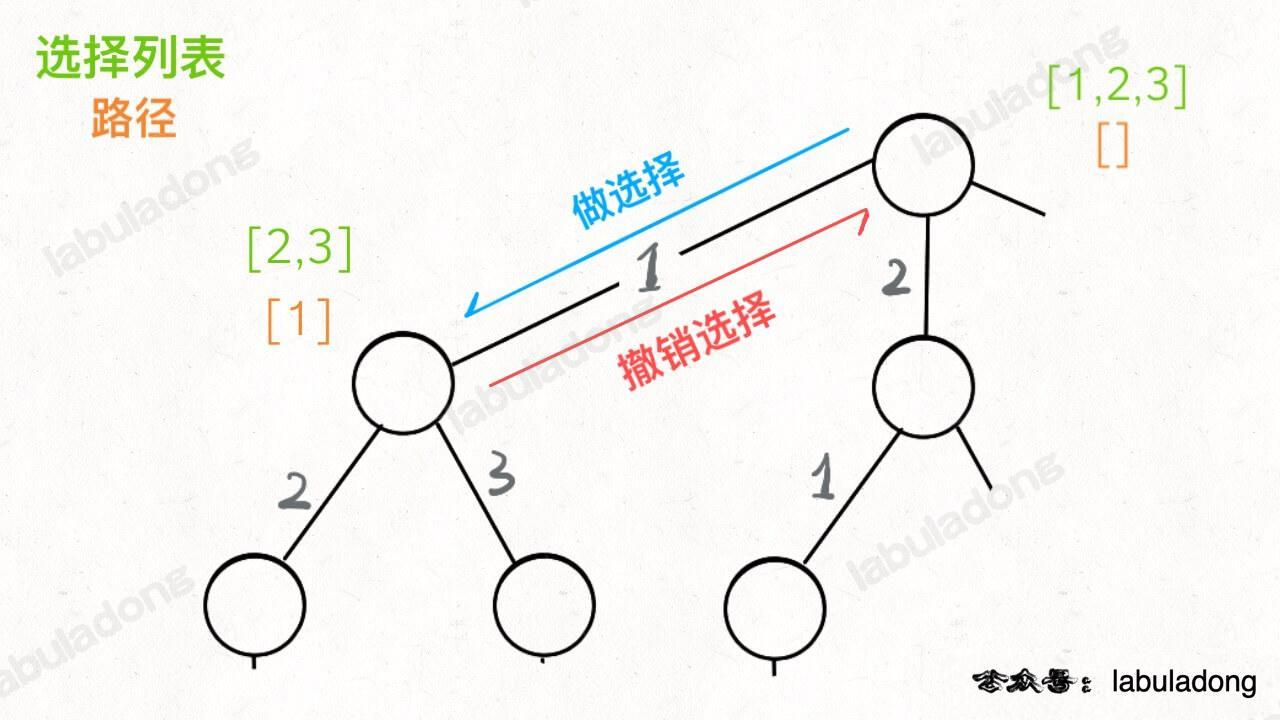
-
🪧代码框架:
result = [] def backtrack(路径, 选择列表): if 满足结束条件: result.add(路径) return for 选择 in 选择列表: 做选择 backtrack(路径, 选择列表) 撤销选择 -
backtrack函数就相当于游走在这颗多叉决策树上的一个指针,它来遍历决策节点,并且做出决策。进入backtrack函数,就以为着我们进入了一个决策节点,也意味着我们需要思考上面所示的三个问题。 -
其核心就是 for 循环里面的递归, 在递归调用之前在这个决策节点上「做选择」,在递归调用之后「撤销选择」
一、51.N 皇后
1.1:题目
力扣链接

1.2:解题思路
-
分析:这题分析用回溯算法来解其实不难。下棋的棋子该落在哪个位置有多种可能(需要满足限制条件),这个棋盘的每一层就相当于决策多叉树的每一层,我们需要遍历这个决策多叉树,进行所有可能的决策,最终把所有解法收集起来,这就是一个回溯的过程。
-
实现:分析出来回溯之后,我们核心是需要写出
backtrack递归函数,它是实现整个回溯遍历的核心。进入到backtrack函数,就相当于进入到一个决策节点,我们必须思考以下3个问题- 当前已经做出选择的路径:可以用一个棋盘存储:
vector <string> board - 选择列表(站在当前决策节点可以做出哪些选择):可以用
row来表示,在board的第row行的每一列是否放置皇后,有n列那么当前该层(行)就有n个选择 - 终止条件:当row<=n时,说明0~n-1行已经全部放置好了函数,当前这个路径(board棋盘)可以作为一个答案被收集
注意的是,不是每一列都可以放置皇后,题目中对皇后的放置有限制条件,所有在遍历选择列表时,对选择需要进行决策可行性判断 (也就是剪枝,代表不能做这个选择)。从这点可以看到,⭐如果不了解回溯算法,一开始感觉会执着于这个限制条件,从而不知道如何下手,但是在决策算法里,它只是一个对决策的限制,我们只需要在遍历到这个决策边时,再进行判断(剪枝)即可。
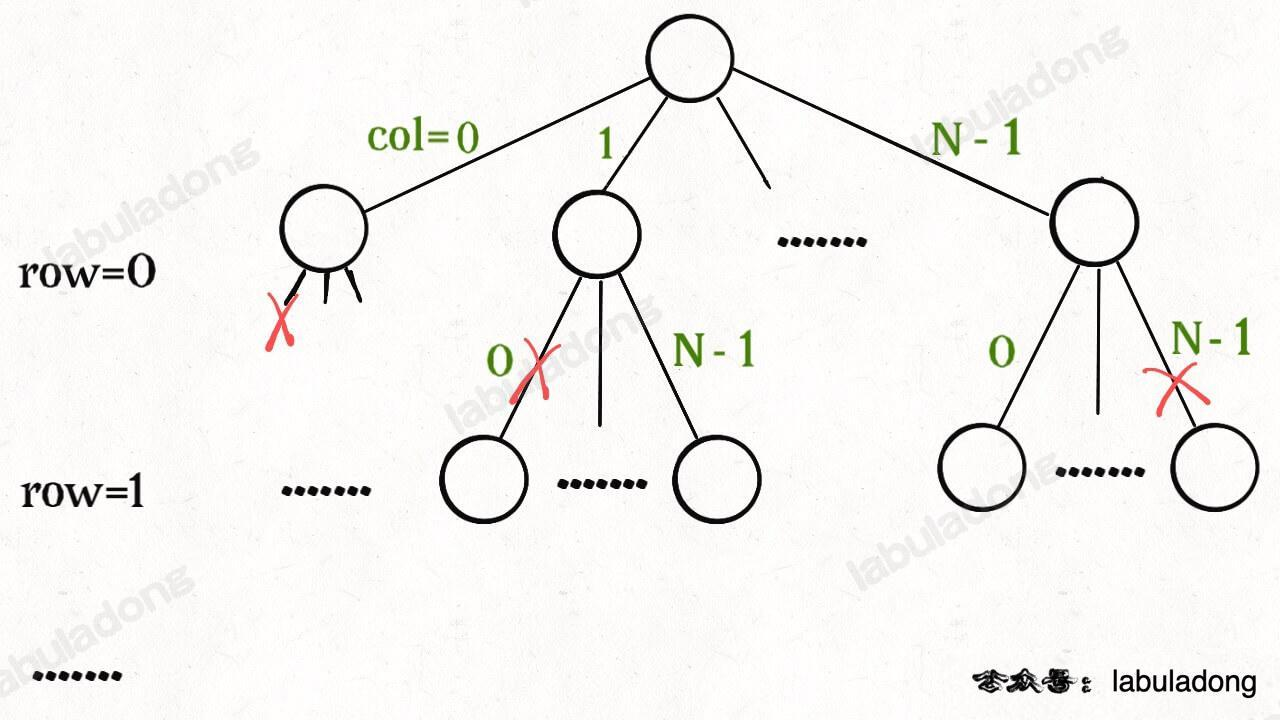
- 当前已经做出选择的路径:可以用一个棋盘存储:
1.3:完整代码
class Solution {
private:
vector<vector<string>> res; //最终答案的收集
/*backtrack函数,相当于游走在这个多叉树每一个决策节点形解空间的一个指针(指向的就是一个决策节点)
作用是来构建这个决策多叉树、遍历多叉树的边(一个边就代表一个选择)和收集答案
- 当前路径:board棋盘用来记录当前路径(在小于row行时做出的选择)
- 选择列表:在board的第row行的每一列是否放置皇后,有n列那么当前该层(行)就有n个选择
- 结束条件:当row<=n时,说明0~n-1行已经全部放置好了皇后,当前这个路径(board棋盘)可以作为一个答案被收集
*/
void backtrack(vector<string> board, int row){
if(row == board.size()){
res.push_back(board);
return;
}
//进行当前决策节点(这一行)的选择遍历
int col = board[row].size();
for (int i = 0; i < col; i++){
/*********前序位置:做出选择(从当前决策节点到下一个决策节点)**************/
//剪枝,如果当前选择不合理
if(!isValid(board, row , i)){
continue;
}
//合理,则做出选择
board[row][i] = 'Q';
/********进入下一个决策节点,接着向下遍历*****************************/
backtrack(board, row+1);
/*********后序位置,撤销当前选择*******************/
board[row][i] = '.';
}
}
/*
剪枝,判断当前(row,col)这个位置放入皇后的话是否合理
*/
bool isValid(vector<string> &board, int row, int col){
//判断列
for(int i =0; i < row; i++){
if(board[i][col] == 'Q') return false;
}
//判断左上方
for(int i =row-1, j =col-1; i >= 0 && j >= 0; i--, j--){
if(board[i][j] == 'Q') return false;
}
//判断右上方
for(int i =row-1, j = col+1; i >= 0 && j < board.size(); i--, j++){
if(board[i][j] == 'Q') return false;
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
vector<string> board(n,string(n, '.')); //存储路径
backtrack(board, 0);
return res;
}
};
二、52. N 皇后 II
2.1:题目
力扣链接
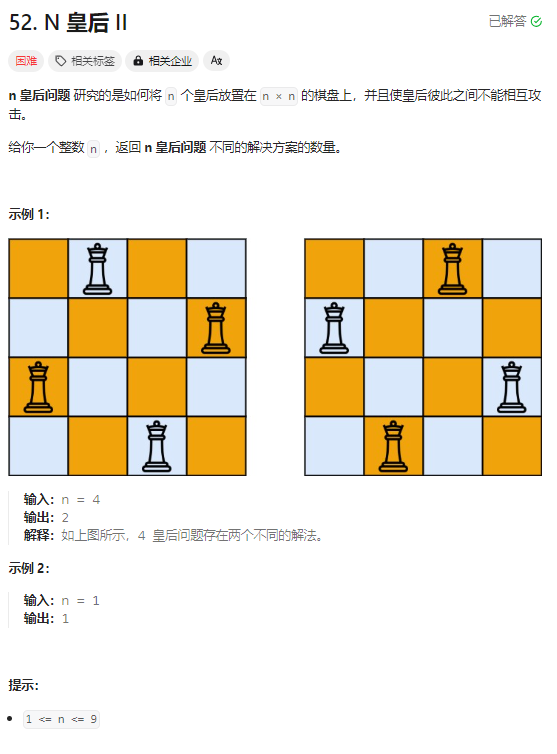
2.2:解题思路
这题解题思路和上面一个一模一样,唯一不同的就是答案收集的变量需要变一下而与!!!之前是存储整个答案,这里的话用一个计数的整形变量ans来存储即可,遍历到底层叶子节点,收集答案ans++即可。
if(row == board.size() ){
ans ++;
return;
}
2.3:完整代码
class Solution {
public:
int ans = 0; //在回溯过程中收集和存储最终答案
/*回溯指针函数backtrack
- 当前路径:由board来记录’
- 选择列表:当前第row行的每一列都是可以选择的
- 结束条件(收集到一个答案): row == board.size()
*/
void backtrack(vector<string>& board, int row){
if(row == board.size() ){
ans ++;
return;
}
//下面进行当前决策节点边的遍历(选择列表中做出选择)
for(int col = 0; col < board.size(); col ++){
//剪枝,如果当前选择不合法,就不继续遍历该决策子节点
if(!isValid(board, row , col)){
continue;
}
/***前序位置:表示做出当前边的决策**/
board[row][col] = 'Q';
//接着向下遍历子决策节点
backtrack(board, row + 1);
/***后序位置,撤销当前决策**********/
board[row][col] = '.';
}
}
bool isValid(vector<string>& board, int row, int col){
//首先判断列
for(int i = row -1; i >=0; i --){
if(board[i][col] == 'Q') return false;
}
//判断左上方
for(int i = row-1, j = col-1; i >=0 && j >= 0; i--, j--){
if(board[i][j] == 'Q') return false;
}
//判断右上方
for(int i = row-1, j = col +1; i >=0 && j <board.size(); i--, j++){
if(board[i][j] == 'Q') return false;
}
return true;
}
int totalNQueens(int n) {
vector<string> board(n, string(n, '.')); //存储当前路径
backtrack(board, 0);
return ans;
}
};