一. 红黑树规则

对于红黑树，进行变色+旋转处理，终究都是为了维持颜色+以下几条规则，只有颜色和规则维持住了，红黑树就维持住了最长路径的长度不超过最短路径的两倍。

规则：

1. 根是黑的。
2. 没有连续的红节点。
3. 每条路径的黑色数量相等。

二. 情况一叔叔存在且为红

注意点：红黑树插入的节点都是红色的，因为在红黑树中动黑色节点是非常忌讳的，因为要维持每条路径黑色数量相等非常困难，所以插入的节点默认都是红色的。

当插入红色节点后：1.如果父亲为黑或者父亲不存在，结束，不需要任何处理。
2. 如果父亲存在且为红，由于插入节点为红，存在连续红节点，需要处理，可以肯定的是爷爷一定是黑，因为插入节点前就是一棵红黑树了，既然父亲和爷爷颜色确定，主要看叔叔。

1.叔叔存在且为红

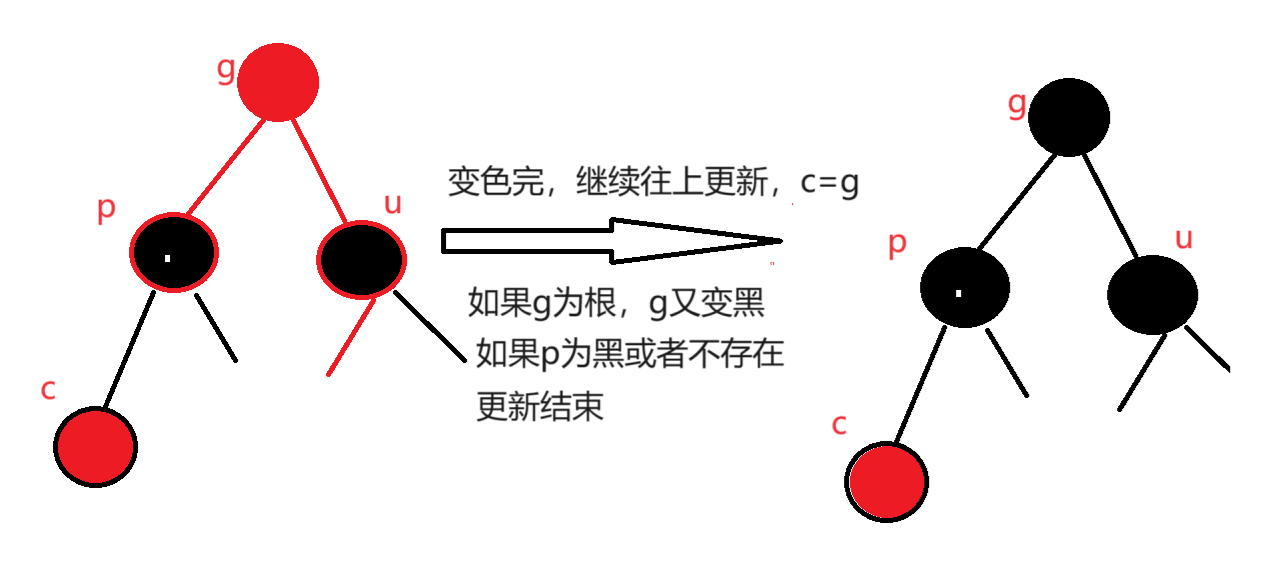
情况二.变色+旋旋

叔叔存在且为黑或者叔叔不存在都需变色+旋转，关键分析是左单旋，右单旋，还是左右双旋，还是右左双旋只要旋转后，就平衡了，直接结束，不需要向上更新

1. 变色+单旋

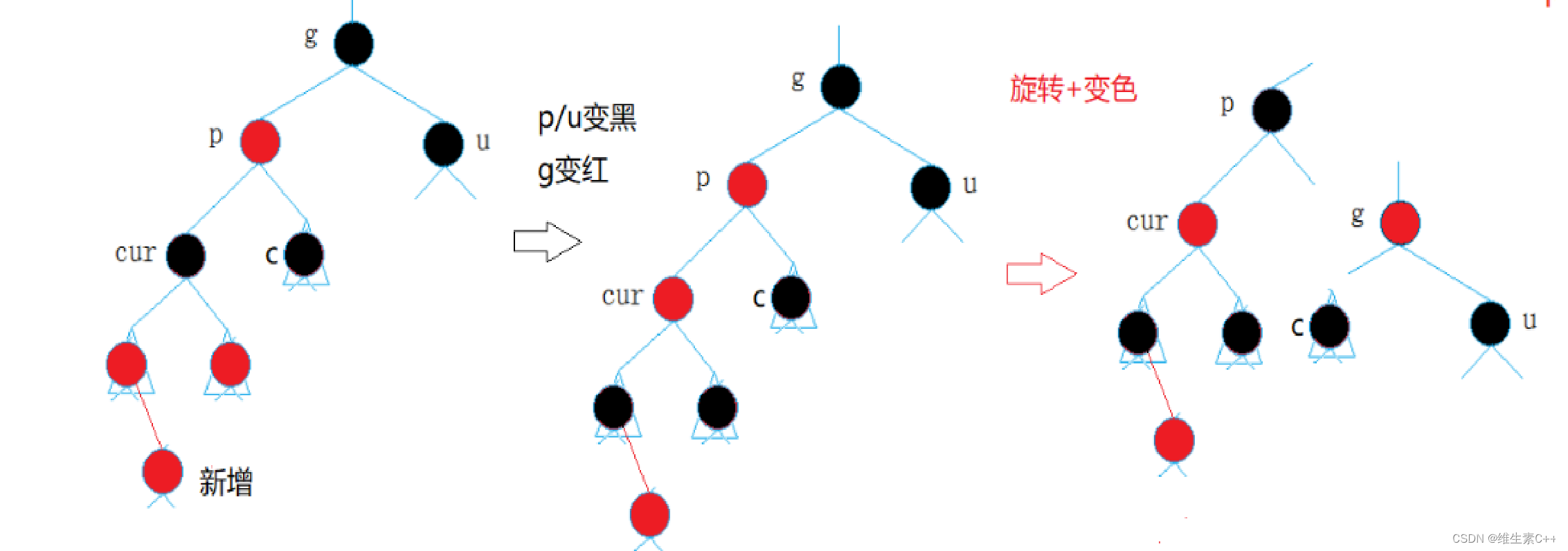
对于叔叔存在且为黑或不存在这种情况，不可能是因为直接插入红色节点导致连续红这种情况直接发生的，因为这发生了，原本就不是红黑树，一定是由上述图一第一种情况处理更新上来导致的。
解决办法：curp->left, pg->left 左左右单旋g点+
p变黑，g变红。
同理：如果上述情况curp->right, pg->right，右右左单旋g点+p变黑，g变红

2.变色+双旋

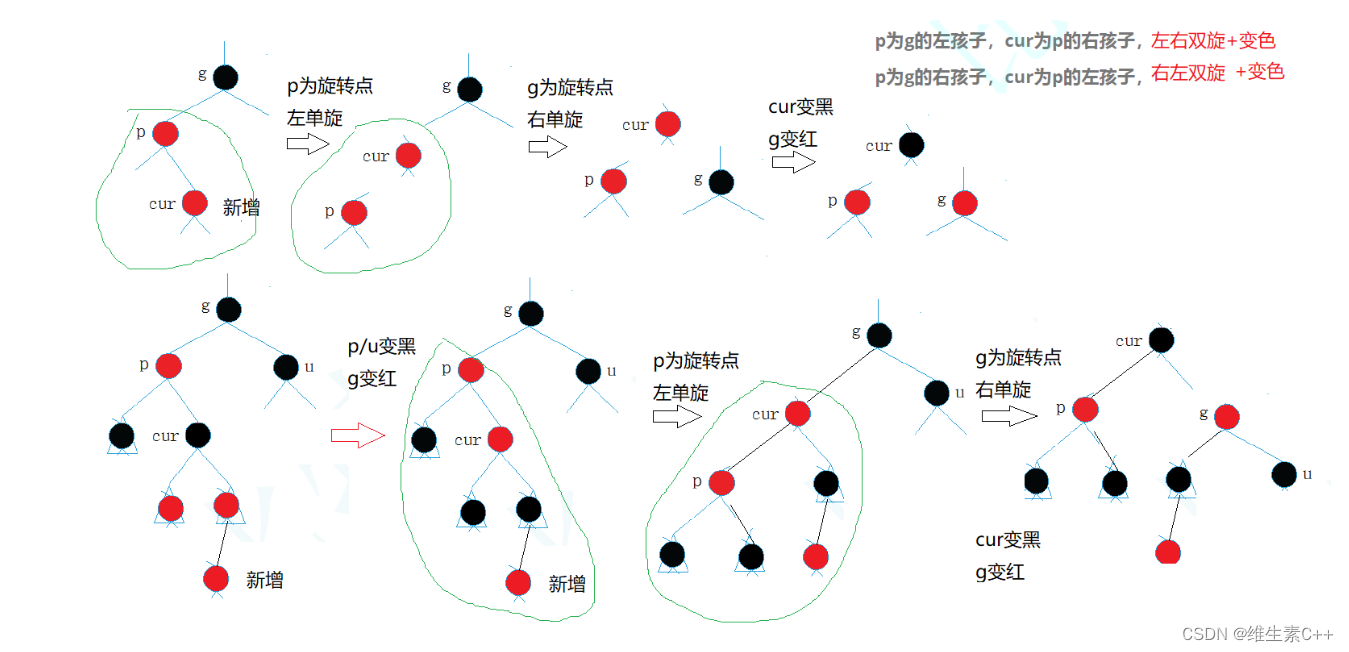
对于这种情况：curp->right, pg->left,左右双旋，
将p左旋，g右旋，+ cur变黑+g变红。

同理：curp->left, pg->right, 右左双旋，将p右旋，g左旋，+cur变黑+g变红

总结单纯变色处理，需要不停向上更新至父亲不存在或者父亲为黑结束，旋转+变色处理完就平衡了直接结束。
一下是代码实现

bool Insert(const pair<K, V>& kv)
		{
			if (_root == nullptr)
			{
				_root = new Node(kv);
				_root->_col = BLACK;	//根为黑色
				return true;
			}

			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_kv.first < kv.first)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_kv.first > kv.first)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			cur = new Node(kv);
			if (parent->_kv.first < kv.first)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
			cur->_parent = parent;
			//父亲存在且为红，连续红节点，处理(如果父亲不存在管你红黑就结束了，如果为黑也结束了）
			while (parent && parent->_col == RED)
			{
				Node* grandfather = parent->_parent;  //算出爷爷，根据父亲为爷爷的左右，确定叔叔
				if (parent == grandfather->_left)
				{
					Node* uncle = grandfather->_right;
					//情况一：叔叔存在且为红 变色处理
					if (uncle && uncle->_col == RED)
					{
						parent->_col = uncle->_col = BLACK;
						grandfather->_col = RED;
						//根节点保证为黑下面处理

						//继续往上处理
						cur = grandfather;
						parent = cur->_parent;
					}
					//情况二：叔叔不存在/叔叔存在且为黑
					else
					{
						//需要判别单旋还是左旋，确定cur的位置
						//旋转+变色
						if (cur == parent->_left)
						{
							//		g
							//	 p		u
							//c
							//左左右单旋
							RotateR(grandfather);
							parent->_col = BLACK;
							grandfather->_col = RED;
						}
						else
						{
							//		g
							//	p		u
							//	   c
							//左右双旋+变色
							RotateL(parent);
							RotateR(grandfather);
							cur->_col = BLACK;
							grandfather->_col = RED;
						}
						break;	//只要旋转结束就平衡了结束
					}
				}
				else
				{
					Node* uncle = grandfather->_left;
					//情况一：叔叔存在且为红 变色处理
					if (uncle && uncle->_col == RED)
					{
						parent->_col = uncle->_col = BLACK;
						grandfather->_col = RED;
						//根节点保证为黑下面处理

						//继续往上处理
						cur = grandfather;
						parent = cur->_parent;
					}
					//情况二：叔叔不存在/叔叔存在且为黑
					else
					{
						if (cur == parent->_right)
						{
							//		g
							//	u		p
							//				c
							RotateL(grandfather);
							parent->_col = BLACK;
							grandfather->_col = RED;
						}
						else
						{
							//		g
							//	u		p
							//		 c
							//右左双旋
							RotateR(parent);
							RotateL(grandfather);
							cur->_col = BLACK;
							grandfather->_col = RED;
						}
						//只要旋转完了，就平衡结束了
						break;
					}
				}
			}
			_root->_col = BLACK;	//变色没有处理根，无论怎么处理都保证根是黑的
			return true;
		}

		void RotateL(Node* parent)
		{
			++rotateSize;
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			parent->_right = subRL;
			if (subRL)
				subRL->_parent = parent;
			subR->_left = parent;
			Node* ppnode = parent->_parent;
			parent->_parent = subR;
			if (_root == parent)
			{
				_root = subR;
				subR->_parent = nullptr;
			}
			else
			{
				if (parent == ppnode->_left)
				{
					ppnode->_left = subR;
				}
				else
				{
					ppnode->_right = subR;
				}
				subR->_parent = ppnode;
			}
		}
		void RotateR(Node* parent)
		{
			++rotateSize;
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			parent->_left = subLR;
			if (subLR)
				subLR->_parent = parent;
			subL->_right = parent;
			Node* ppnode = parent->_parent;
			parent->_parent = subL;
			if (parent == _root)
			{
				_root = subL;
				subL->_parent = nullptr;
			}
			else
			{
				if (parent == ppnode->_left)
				{
					ppnode->_left = subL;
				}
				else
				{
					ppnode->_right = subL;
				}
				subL->_parent = ppnode;
			}
		}
		

无论怎么方式处理完都需要保证根是黑的，最后加上