【NOIP普及组】税收与补贴问题
|
💖The Begin💖点点关注,收藏不迷路💖
|
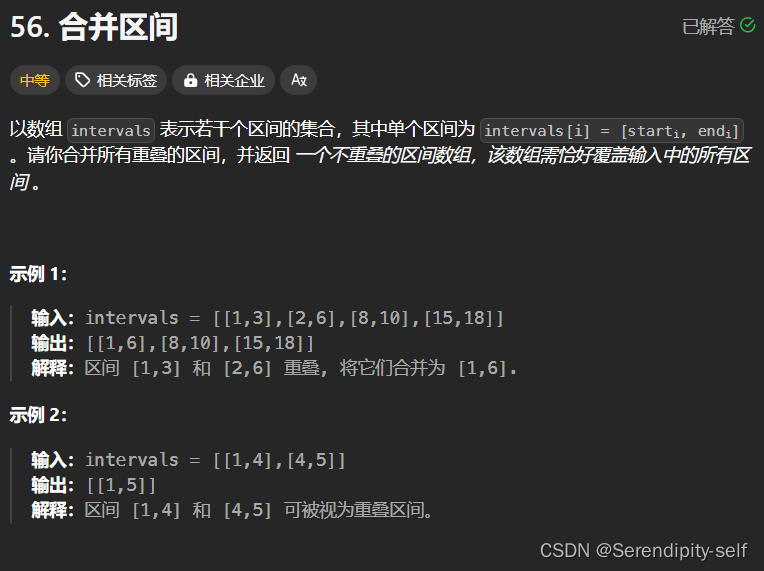
每样商品的价格越低,其销量就会相应增大。现已知某种商品的成本及其在若干价位上的销量(产品不会低于成本销售),并假设相邻价位间销量的变化是线性的且在价格高于给定的最高价位后,销量以某固定数值递减。(我们假设价格及销售量都是整数)
对于某些特殊商品,不可能完全由市场去调节其价格。这时候就需要政府以税收或补贴的方式来控制。(所谓税收或补贴就是对于每个产品收取或给予生产厂家固定金额的货币)问题求解:
你是某家咨询公司的项目经理,现在你已经知道政府对某种商品的预期价格,以及在各种价位上的销售情况。要求你确定政府对此商品是应收税还是补贴的最少金额(也为整数),才能使商家在这样一种政府预期的价格上,获取相对其他价位上的最大总利润。
总利润=单位商品利润*销量
单位商品利润=单位商品价格-单位商品成本(-税金 or +补贴)
输入:
第一行为政府对某种商品的预期价,第二行有两个整数,第一个整数为商品成本,第二个整数为以成本价销售时的销售量,以下若干行每行都有两个整数,第一个为某价位时的单价,第二个为此时的销量,以一行-1,-1表示所有已知价位及对应的销量输入完毕,输入的最后一行为一个单独的整数表示在已知的最高单价外每升高一块钱将减少的销量。
输出:
输出有两种情况:若在政府预期价上能得到最大总利润,则输出一个单独的整数,数的正负表示是补贴还是收税,数的大小表示补贴或收税的金额最小值。若有多解,取绝对值最小的输出。
如在政府预期价上不能得到最大总利润,则输出“NO SOLUTION”。
样例输入:
31
28 130
30 120
31 110
-1 -1
15
样例输出:
4
#include <stdio.h>
#include <stdlib.h>
#define N 100005 // 定义数组长度的常量
typedef struct { // 定义节点结构体
int c, num; // c表示单价,num表示销量
} Node;
int targetC, targetNum, cut, cnt; // targetC为政府预期价,targetNum为政府预期价对应的销量,cut为每升高一块钱将减少的销量,cnt表示数组中节点个数
Node nodes[N]; // 定义节点数组
int compare(const void *a, const void *b) { // 定义比较函数
return ((Node*)b)->num - ((Node*)a)->num; // 根据销量从大到小排序
}
void solve() { // 求解最优税收或补贴的函数
int ans = 0, p, q, x, y; // ans表示税收或补贴的金额,p、q、x、y都是中间变量
int flag1 = 0, flag2 = 0; // flag1、flag2表示是否需要进行税收或补贴
while (1) { // 迭代直到得到最优解
flag1 = 0, flag2 = 0;
p = (targetC - nodes[0].c + ans) * targetNum; // 计算政府预期价下,所有节点的总销售额(不考虑税收或补贴)
q = (targetC - nodes[0].c - ans) * targetNum; // 计算政府预期价下,所有节点的总销售额(不考虑税收或补贴)
for (int i = 0; i < cnt; i++) { // 遍历所有节点
if (nodes[i].num <= 0) // 如果该节点销量为0,跳出循环
break;
x = (nodes[i].c - nodes[0].c + ans) * nodes[i].num; // 计算该节点在政府预期价下的总销售额(不考虑税收或补贴)
y = (nodes[i].c - nodes[0].c - ans) * nodes[i].num; // 计算该节点在政府预期价下的总销售额(不考虑税收或补贴)
if (x > p) // 如果该节点在政府预期价下销售额高于所有节点的总销售额,需要进行补贴
flag1 = 1;
if (y > q) // 如果该节点在政府预期价下销售额低于所有节点的总销售额,需要进行税收
flag2 = 1;
if (flag1 && flag2) // 如果需要进行补贴和税收,则跳出循环
break;
}
if (flag1 && flag2) { // 如果需要进行补贴和税收,则增加税收或补贴的金额
ans++;
continue;
}
x = nodes[cnt-1].c; // 获取最高价位
y = nodes[cnt-1].num; // 获取最高价位对应的销量
while (y > 0) { // 不断增加税收或补贴的金额,直到找到最优解
x++; // 增加单价
y -= cut; // 减少销量
if ((x - nodes[0].c + ans) * y > p) // 如果补贴金额太小导致总销售额低于政府预期价下的总销售额,需要进行补贴
flag1 = 1;
if ((x - nodes[0].c - ans) * y > q) // 如果税收金额太小导致总销售额高于政府预期价下的总销售额,需要进行税收
flag2 = 1;
if (flag1 && flag2) // 如果需要进行补贴和税收,则跳出循环
break;
}
if (flag1 && !flag2) { // 如果需要进行补贴但不需要进行税收,则输出补贴金额
printf("%d\n", -ans);
return;
}
if (!flag1 && flag2) { // 如果需要进行税收但不需要进行补贴,则输出税收金额
printf("%d\n", ans);
return;
}
if (!flag1 && !flag2) { // 如果不需要进行补贴和税收,则输出0
printf("%d\n", ans);
return;
}
ans++; // 增加税收或补贴的金额
}
}
int main() { // 主函数
scanf("%d", &targetC); // 输入政府预期价
int x, y;
while (1) { // 输入所有节点
scanf("%d %d", &x, &y);
if (x == -1 && y == -1) // 如果输入-1,-1则结束输入
break;
nodes[cnt].c = x;
nodes[cnt].num = y;
cnt++;
}
scanf("%d", &cut); // 输入每升高一块钱将减少的销量
qsort(nodes, cnt, sizeof(Node), compare); // 对节点按销量从大到小排序
for (int i = 0; i < cnt - 1; i++) { // 补全缺失的节点
if (nodes[i+1].c - nodes[i].c > 1) { // 如果两个节点之间存在空缺
for (int j = nodes[i].c + 1; j < nodes[i+1].c; j++) { // 在两个节点之间插入节点
nodes[cnt].c = j;
nodes[cnt].num = nodes[i].num - (nodes[i].num - nodes[i+1].num) / (nodes[i+1].c - nodes[i].c) * (j - nodes[i].c);
cnt++;
}
}
}
qsort(nodes, cnt, sizeof(Node), compare); // 再次对节点按销量从大到小排序
int targetExists = 0;
for (int i = 0; i < cnt; i++) { // 查找政府预期价对应的销量
if (nodes[i].c == targetC) {
targetExists = 1;
targetNum = nodes[i].num;
break;
}
}
if (!targetExists) // 如果政府预期价对应的销量不存在,需要根据最高价位和每升高一块钱将减少的销量来计算
targetNum = nodes[cnt-1].num - (targetC - nodes[cnt-1].c) * cut;
solve(); // 求解最优税收或补贴
return 0;
}
求解最优税收或补贴的问题。主要思想如下:
- 定义节点结构体,包含单价和销量两个属性。
- 定义全局变量,包括政府预期价、政府预期价对应的销量、每升高一块钱将减少的销量等。
- 输入政府预期价和节点信息,并对节点按销量从大到小进行排序。
- 补全可能存在的节点缺失,并再次按销量从大到小进行排序。
- 查找政府预期价对应的销量,如果不存在,则根据最高价位和每升高一块钱将减少的销量来计算。
- 使用solve函数求解最优税收或补贴。迭代过程中,比较各节点在政府预期价下的销售额与所有节点总销售额的大小,判断是否需要进行补贴和税收。增加税收或补贴的金额,直到找到最优解。
- 输出最优税收或补贴的金额。
总体来说,该代码通过迭代的方式,不断调整税收或补贴的金额,直到找到最优解。

|
💖The End💖点点关注,收藏不迷路💖
|