目录
##什么是区间调度问题
##贪心解法
##具体的例题示例讲解
##452. 用最少数量的箭引爆气球 - 力扣(LeetCode)
##435. 无重叠区间 - 力扣(LeetCode)
##56. 合并区间 - 力扣(LeetCode)
##什么是区间调度问题
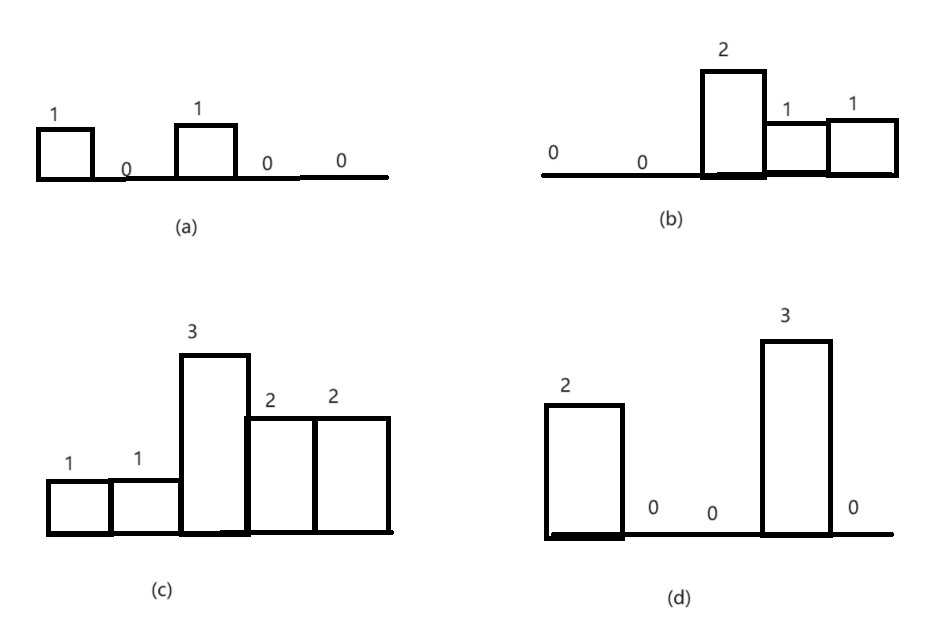
区间调度问题是一个经典的贪心算法问题:
通常描述为:给定一组活动,每个活动都有一个开始时间和结束时间。只有一个活动能在同一时间段内进行。目标是找到最大数量的互不相交的活动。
##贪心解法
- 从区间集合 intvs 中选择一个区间 x,这个 x 是在当前所有区间中结束最早的(开始最早)。
- 把所有与 x 区间相交的区间从区间集合 intvs 中删除。
- 重复步骤 1 和 2,直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。
##具体的例题示例讲解
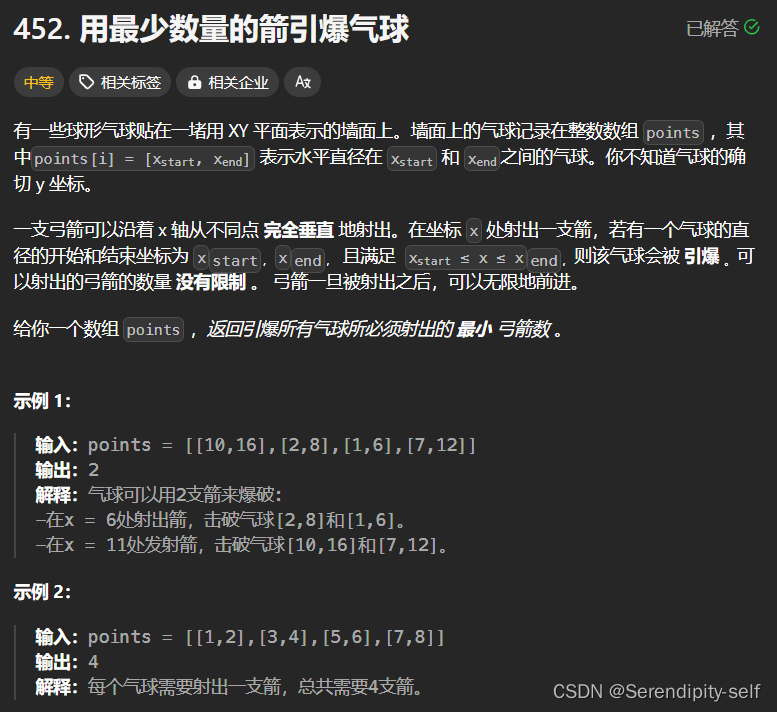
##452. 用最少数量的箭引爆气球 - 力扣(LeetCode)
##思路
1.第一步按照最先开始时间排序(结束最早)
2.然后开始遍历数组,找到有交集的区间,进行修改
3.将当前位置的结束区间和上一个跟当前有交集的结束区间的最小值赋值给当前位置的结束区间
4.样例解释{first:[1,4],[2,3],result:[1,4],[2,3]; second:[1,5],[2,6],result:[1,5],[2,5],third:[1,3],[2,3],result:[1,3],[2,3]}
5.解释以下second:
当然下面一个气球有可能和上面两个气球都重合,如果只和上面一个气球重合而不和上上面气球重合的话,那么还需要额外的一支箭去引爆。
为了实现判断,当两支气球重合时,我们可以把右边界缩小为两个气球右边界较小的一个值(因为此时新气球的左边界一定大于等于上面两个气球的左边界,所以不用判断),如果新气球左边界小于上面气球的右边界,那么就不需要额外的箭就能引爆。
##代码示例
//c++代码示例 class Solution { public: int findMinArrowShots(vector<vector<int>>& points) { if (points.size() == 0) { return 0 ; } sort(points.begin(),points.end(),[](const vector<int>& a,const vector<int>& b) { return a[0] < b[0] ; }) ; int ans = 1 ; for (int i = 1 ; i < points.size() ; i++) { if (points[i][0] <= points[i-1][1]) { points[i][1] = min(points[i][1],points[i-1][1]) ; } else { ans++ ; } } return ans ; } };//python代码示例 class Solution: def findMinArrowShots(self, points: List[List[int]]) -> int: points.sort(key = lambda x : x[0] ,reverse =False) if len(points) == 0 : return 0 ans = 1 for i in range(1,len(points)) : if (points[i][0] <= points[i-1][1]) : points[i][1] = min(points[i][1],points[i-1][1]) else : ans += 1 return ans
##435. 无重叠区间 - 力扣(LeetCode)
##思路
跟上一个题目的思路一样
具体的细节:当本区间左边界比上一个区间右边界小的时候我们就需要去删除了。删除在代码上只需要将此区间右边界设置为此区间与上一个区间中的较小值就可以了。如果此区间左边界大于等于上一个区间右边界,那么就证明两个区间没有重合,不需要进行操作。
##代码示例
//c++代码示例 class Solution { public: int eraseOverlapIntervals(vector<vector<int>>& intervals) { sort(intervals.begin(),intervals.end(),[](const vector<int>& a,const vector<int>& b) { return a[0] < b[0] ; }) ; int ans = 0 ; for (int i = 1 ; i < intervals.size() ; i++) { if (intervals[i][0] < intervals[i-1][1]) { intervals[i][1] = min(intervals[i-1][1],intervals[i][1]) ; ans++ ; } } return ans ; } };//python代码示例 class Solution: def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int: intervals.sort(key = lambda x : x[0] ,reverse = False) if (len(intervals) == 0) : return 0 ans = 0 for i in range(1,len(intervals)) : if (intervals[i][0] < intervals[i-1][1]) : intervals[i][1] = min(intervals[i][1],intervals[i-1][1]) ans += 1 return ans
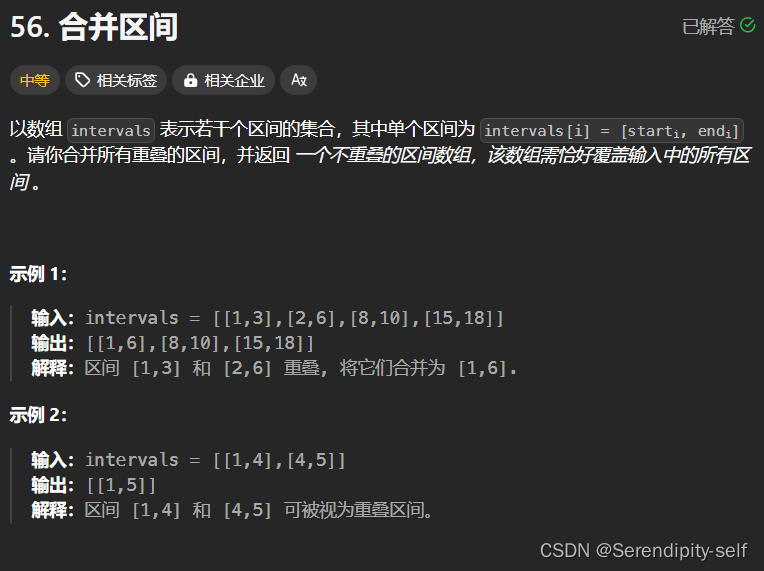
##56. 合并区间 - 力扣(LeetCode)
##思路
先进行排序,然后用此区间左边界与上一个区间右边界进行比较,如果满足重叠,则进行记录。
##代码示例
//c++代码示例 class Solution { public: vector<vector<int>> merge(vector<vector<int>>& intervals) { vector<vector<int>> ans ; sort(intervals.begin(),intervals.end(),[](const vector<int>& a,const vector<int>& b) { return a[0] < b[0] ; }) ; for (int i = 0 ; i < intervals.size() ; i++) { if (!ans.empty() && intervals[i][0] <= ans[ans.size()-1][1]) { ans[ans.size()-1] = {min(ans[ans.size()-1][0],intervals[i][0]),max(ans[ans.size()-1][1],intervals[i][1])} ; } else { ans.push_back({intervals[i][0],intervals[i][1]}) ; } } return ans ; } };//python代码示例 class Solution: def merge(self, intervals: List[List[int]]) -> List[List[int]]: ans = [] intervals.sort(key=lambda x: x[0]) for i in range(len(intervals)): if ans and intervals[i][0] <= ans[-1][1]: ans[-1] = [min(ans[-1][0], intervals[i][0]), max(ans[-1][1], intervals[i][1])] else: ans.append([intervals[i][0], intervals[i][1]]) return ans