前言

  因为课程需要，第一次这么彻底地接触numpy。虽闻名已久，但是真正使用numpy才感受到它的强大，发现它尤其适合数据分析与处理。这里根据自己的使用经验简单总结一下numpy在矩阵运算中的应用，之后也会根据自己的实践经历不断更新。

0 遇事不决，先查官网，查着查着就查熟了

• numpy中文官网：https://www.numpy.org.cn/reference/
• numpy英文官网：https://numpy.org/doc/stable/

建议主要参考英文官网，中文官网翻译有点生硬的感觉。。。

补充教程：numpy速查手册

1 矩阵运算及其必要性

  所谓的数据处理，其本质大都可以归为矩阵运算。因为需要处理的数据大都是矩阵或向量的形式，因此个人认为一个工具适不适合做数据处理，一个重要的指标的就是支不支持矩阵运算，因为如果没有矩阵运算，循环去处理一大堆数据势必会造成运行过长的问题。而这也是为什么很多人会推荐在使用python处理数据的时候不要用它自带的list，而要用numpy。
  一般提到矩阵运算，我们首先想到的就是MATLAB（因为我是先接触的MATLAB~~），因此本文想对标MATLAB中的语法和使用来对比学习 python中的numpy库。

如果对MATLAB中矩阵运算不熟悉的同学可以看一下我之前的一篇博客。

意外发现其实numpy官网也有一个专门的教程来给熟悉MATLAB的开发人员看的，链接在这里。

2 矩阵的创建

2.1 普通矩阵

  numpy中创建矩阵的方式非常单一，一般就是使用np.array：

import numpy as np
A = np.array([1,2,3])
# 参数还可以是一个已有的list类型
B = np.array(list_b)

如果要创建二维甚至多维矩阵，则可以利用中括号分隔，如下所示：

import numpy as np
C = np.array([[1,2,3],
			[2,3,4]])

即中括号是分隔维度。
  其实，array函数内部的参数可以非常复杂，具体可以看看官网。但是一般来说，最多就是再指定数组中元素的数据类型：

>>> np.array([1, 2, 3], dtype=complex)
array([ 1.+0.j,  2.+0.j,  3.+0.j])

  此外，还需要注意的是，使用 np.array 创建的矩阵其 数据类型 为 np.ndarray ，这个在类型注解时需要注意。

对比MATLAB：
  在MATLAB中，创建矩阵是通过空格或逗号来区分同一行的不同元素，用分号来区分不同行，如果创建高维矩阵（>2）不能简单地套中括号，而应该使用专门的函数来进行创建。

2.2 特殊矩阵

  和MATLAB一样，numpy也支持创建一些特殊矩阵：

• 零矩阵：np.zeros()
• 单位矩阵：np.eye()

3 矩阵的索引

  python中的数据索引，不同的数据类型有不同的运算符。

3.1 str, list, tupple的索引

参考链接

  对这些python自带的数据类型，索引数据时除了单独索引某个数据外，剩下的就只需要了解冒号运算符即可。
  冒号运算符的固定结构就是[start : stop : step]，先来看几个例子理解一下。

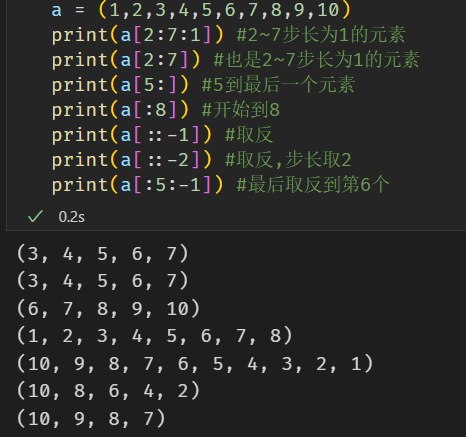
再来总结一下上面的规律：上面的表达式[start : stop : step]当中有三个变量，其实可以把它们都视为函数的参数，且都含有默认值：
其中step参数默认值就是1；
start参数的默认值则为0，即整个序列的起点；
而stop参数默认则为序列的终点。
除此之外，step参数最为特殊，即它可以为负值，相当于将其输出的序列顺序反过来，其间隔仍然为step的绝对值。而且，如果step参数取默认值，除不写该参数外，第二个冒号也可以省略。

3.2 numpy索引

  对于numpy的数组，其索引方式更加丰富。除了具有以上所有的索引方式外，numpy还多出一些索引方式，这里简单总结为三点：

• 逗号运算符
  如果需要索引的数组为一个二维及以上的数组，如果是python自带的数据类型，只能是使用多个中括号的方式，但是对于numpy的数组，还可以采用逗号运算符，用来区分维度。如下所示。
  

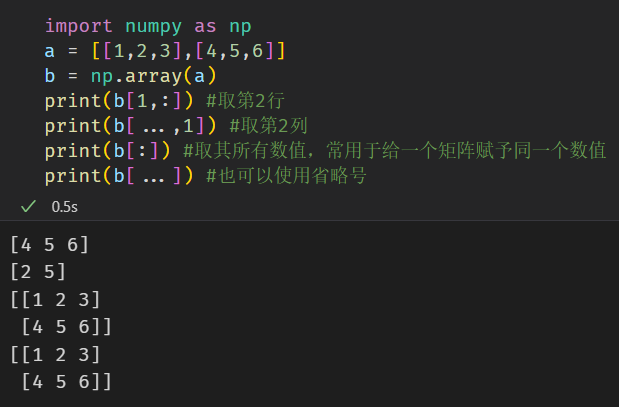
• 省略号运算符及冒号运算符
  如果要取二维数组的某一行或某一列时，就涉及到需要取一整个维度的问题，可以采用省略号或冒号来实现，如下所示。
  

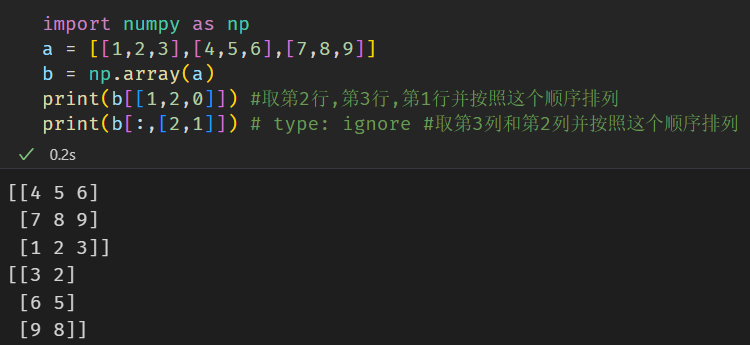
• 列表索引（花式索引）
  对于numpy数组来说，除了使用上述的特殊符号外，还可以传入特定的向量，如下所示。
  
  换一种角度来看，其实上面传递的都可以视为一个列表，只是不是特别明显罢了。

对比MATLAB：
  在MATLAB中，矩阵的索引是通过圆括号来实现的，支持逗号运算符和花式索引，对于冒号运算符，其结构为[start : step : stop]，如果要反序，除step赋值为负数外，还需要将start和stop交换顺序。而且MATLAB当中有一个end的宏变量，指定某一维的末尾。

4 矩阵的运算

4.1 通用函数与广播机制

  在学习numpy中矩阵运算规律前，最好要先了解一下numpy中的通用函数与广播机制。这也是贯穿numpy矩阵运算所有的重要内容。
  所谓通用函数，是指能够同时对元素内所有元素逐个进行运算的函数。numpy当中几乎所有的计算函数都是通用函数，具体有哪些内容可以参考这篇博客。
  使用通用函数有一个非常大的好处就是本来需要循环遍历的列表可以一次性传入函数，大大节约了运算时间，此即向量化的思想。
  而所谓广播机制，个人认为可以从两方面来理解。

• 对于需要传入单个参数的函数（f(x)）来说，如果传入的是多个“单个参数”组成的列表（[x1,x2,…]），那么函数将逐个取值并代入计算，最后返回值也将是原来输出值组成的列表（[f1,f2,…]）。
• 对于算术运算符来说，如f(x1, x2) = x1 + x2，如果传入的参数维度不一致，那么函数会通过广播机制将输入的参数的维度变为一致。

  这里第一种情形比较好理解，关键在于理解第二种。需要明确的是，广播机制并适用于传入任意维度的参数，并不是简单粗暴地取公倍数。常见的有下面这4种类型。（m*n表示m行n列，左边为A，右边为B）

• m*n + m*1 = m*n ：相当于A的每一行的每一个数都加上B对应行的那个离散点；
• m*n + 1*n = m*n：相当于A的每一行都和B相加；
• m*n + 1*1 = m*n：相当于A的每个元素都加上B这个离散点；
• 1*n + m*1 = m*n：相当于A的每一列都需要加上B这一行。

总结来看，两个向量能够应用广播机制的要求是在至少存在某一维，要么两个数值相等，要么有一个值为1
  以上是从矩阵的角度来理解，还可以考虑从列表的角度来理解。即把所有的参数都理解为列表。对于二维数组，可以理解为列表的列表。两个列表相加时，如果维度不同，维度高的需要先降维拆分，直到可以计算为止。如果发现即使降维拆分也无法满足可以计算的要求，则程序报错。

对比MATLAB：
  在MATLAB中，矩阵加减法也支持广播机制。

4.3 矩阵乘法

  关于矩阵乘法，有两个概念很有意思，叫做矩阵叉乘和矩阵点乘。所谓叉乘就是一般的矩阵乘法，即前一个矩阵的列数要等于后一个矩阵的行数；而所谓矩阵点乘就是矩阵中每个对应元素相乘，要求两个矩阵同型，乘出来的矩阵大小不变。考虑到这两种运算非常常见，这里做了一个表，来对比python和MATLAB

–	Python	MATLAB
矩阵乘法（叉乘）	np.dot(A, B)	A*B
矩阵点乘（对应元素相乘）	A*B or np.multiply(A,B)	A.*B

4.4 矩阵求逆

• python：np.linalg.inv(A)

• MATLAB: inv(A)
  

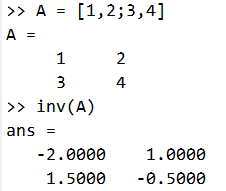
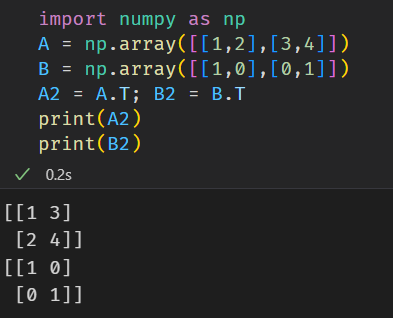
4.5 矩阵转置

  对numpy的数组，想要实现转置非常简单，直接在矩阵的后面加上.T即可。示例如下：

4.6 向量合并

  在进行数据处理时，经常会遇到一种需求那就是将多个列表合并成为一个矩阵。
  先来看看python中自带的列表是怎么操作的。对于list，如果想要合并成为一个大的列表，可以采用+或extend函数，如下所示。

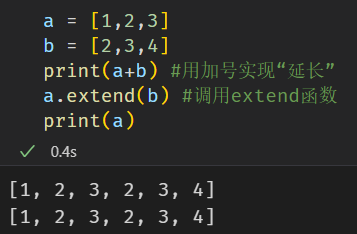
如果想要合成为一个矩阵，即列表的列表，也非常简单，直接用中括号连接即可。如下所示。

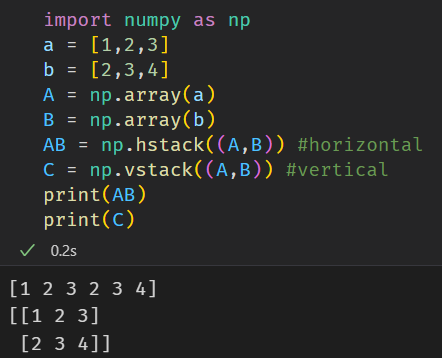
  再来看看numpy是怎么实现的。

除此之外，还可以使用其自带的vstack和hstack函数来构建矩阵。

4.7 形状变换

  在numpy中，如果想要只改变矩阵的形状而不改变数据时，可以使用reshape函数。这里有两种使用方式：

import numpy as np
s = np.array([1,2,3,4,5,6])
# 第一种方法:复制一份
np.reshape(s,(3,2)) #需要注意，这里的大小一定要是合理的，否则会报错
# 第二种方法:直接在原来数组上修改
s.reshape(2,3)

  值得一提的是，第二种直接修改的方式在传参时，是支持解包的，即可以传(2,3)，也可以传2,3，非常方便。

补充教程：python 中 numpy 模块的 size,shape, len的用法

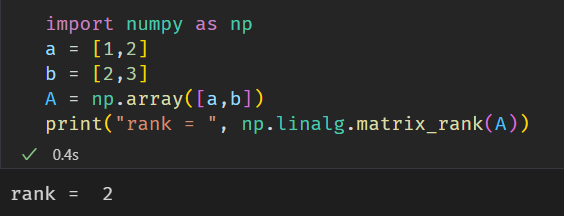
4.8 方阵的行列式和秩

  在numpy中也可以求方阵的行列式和秩，其函数包含在其线性代数库linalg中，使用方式如下图所示。

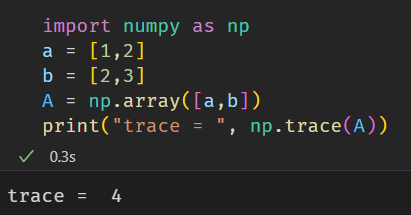
4.9 方阵的迹

  所谓方阵的迹，是指主对角线元素之和，在numpy中使用方式如下所示。

4.10 解线性方程

  在numpy中还可以解线性方程，对于形式如$AX=b$的线性方程，使用numpy解方程的方式如下所示。

5 其他边角知识

• NumPy 获取唯一元素、出现次数、展平数组
• numpy 统计数组的值出现次数与np.bincount()详细解释