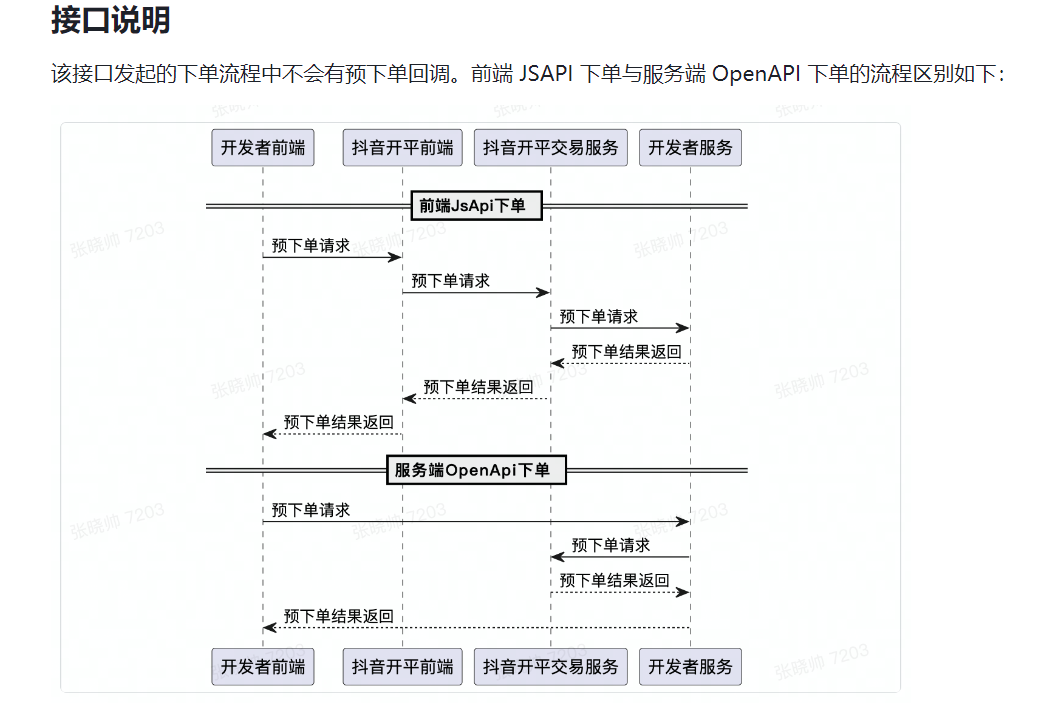
选择就像是在谱曲,每个决定就是一个音符,只有将它们有序地安排在一起,才能奏响美妙的乐章。
文章目录
- 一、选择排序的思想
- 二、选择排序的发展历程
- 三、选择排序具象化
- 四、选择排序算法实现
- 五、选择排序的特性
- 推荐阅读
一、选择排序的思想
选择排序(Selection Sort)是一种简单直观的排序算法。它的基本思想是,每次从待排序的数据元素中选择最小(或最大)的一个元素,放到已排序序列的末尾,直到所有元素均排序完毕。
这个过程可以用下面的步骤来描述:
- 首先,在待排序序列中找到最小(或最大)的元素,将其与序列中的第一个元素交换位置,这样最小(或最大)的元素就放到了序列的第一个位置。
- 然后,在剩余的未排序序列中,找到最小(或最大)的元素,将其与序列中的第二个元素交换位置,这样第二小(或第二大)的元素就放到了序列的第二个位置。
- 依此类推,重复以上步骤,直到所有元素都排序完毕。
选择排序的特点是简单直观,实现也比较容易,但是由于每次都要在剩余的未排序序列中查找最小(或最大)的元素,所以其时间复杂度较高,为 O ( n 2 ) O(n^2) O(n2)。因此,选择排序适用于数据量较小的情况。
二、选择排序的发展历程
选择排序是一种简单直观的排序算法,其发展历史可以追溯到 20 世纪初期。
- 早期方法:选择排序的基本思想可以追溯到早期的人工排序方法。在计算机出现之前,人们就已经使用手工方法对物品进行排序,例如根据尺寸或其他属性进行选择和排列。
- 算法形式化:选择排序的第一个严格定义可以追溯到 20 世纪 50 年代。这时,计算机科学家开始将排序算法形式化为算法和程序。选择排序作为最简单的排序算法之一,很快就被提出并研究。
- 早期计算机应用:随着计算机的发展,选择排序成为早期计算机应用中常用的排序算法之一。虽然它不是最有效的排序算法,但它的简单性和直观性使得它在早期的计算机系统中得到了广泛应用。
三、选择排序具象化
场景假设:我们需要将下图序列使用选择排序按从小到大进行排序。
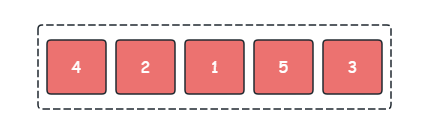
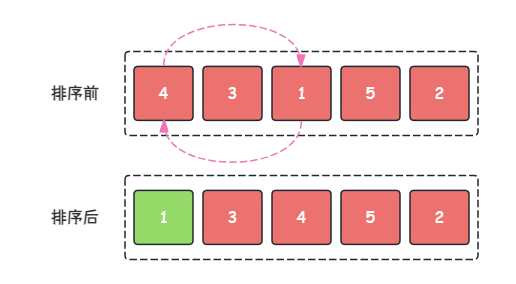
- 第 1 1 1 趟:在当前序列中找到最小的元素即 1 1 1 与第 1 1 1 个元素(即: 4 4 4)交换位置
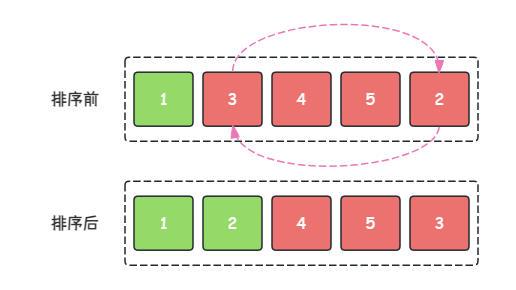
- 第 2 2 2 趟:在当前序列中找到最小的元素即 2 2 2 与第 2 2 2 个元素(即: 3 3 3)交换位置
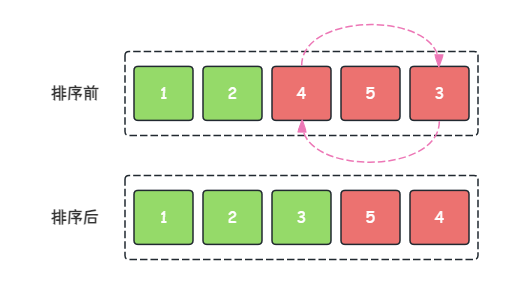
- 第 3 3 3 趟:在当前序列中找到最小的元素即 3 3 3 与第 3 3 3 个元素(即: 4 4 4)交换位置
- 第 4 4 4 趟:在当前序列中找到最小的元素即 4 4 4 与第 4 4 4 个元素(即: 5 5 5)交换位置
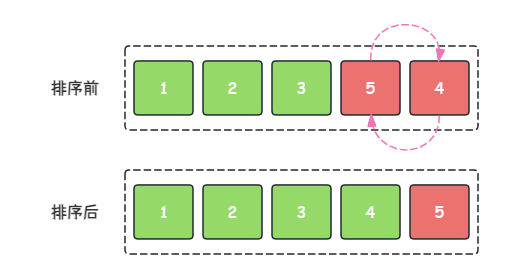
- 第 5 5 5 趟:不需要做任何操作,因为所有元素已排序好

我们可以发现:其实
n
n
n 个元素,只需要
n
−
1
n - 1
n−1 趟选择就可以完成排序。
四、选择排序算法实现
// 选择排序算法实现
public void selectionSort(int[] arr) {
int n = arr.length; // 获取数组长度
// 外层循环,遍历数组中的每个元素(除最后一个元素)
for (int i = 0; i < n - 1; i++) {
int minIndex = i; // 假设当前位置为最小值的索引
// 内层循环,在未排序的部分中找到最小值的索引
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) { // 如果当前元素比最小值还小
minIndex = j; // 更新最小值的索引
}
}
// 将找到的最小值与当前位置的元素交换
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
算法时间复杂度分析:
| 情况 | 时间复杂度 | 计算公式 |
|---|---|---|
| 最好情况 | O ( n 2 ) O(n^2) O(n2) | T ( n ) = ∑ i = 1 n ( n − i + 1 ) = n ( n + 1 ) 2 = O ( n 2 ) T(n) = \sum_{i = 1}^{n}(n - i + 1) = \frac{n(n + 1)}{2} = O(n^2) T(n)=∑i=1n(n−i+1)=2n(n+1)=O(n2) |
| 平均情况 | O ( n 2 ) O(n^2) O(n2) | T ( n ) = ∑ i = 1 n ( n − i + 1 ) = n ( n + 1 ) 2 = O ( n 2 ) T(n) = \sum_{i = 1}^{n}(n - i + 1) = \frac{n(n + 1)}{2} = O(n^2) T(n)=∑i=1n(n−i+1)=2n(n+1)=O(n2) |
| 最坏情况 | O ( n 2 ) O(n^2) O(n2) | T ( n ) = ∑ i = 1 n ( n − i + 1 ) = n ( n + 1 ) 2 = O ( n 2 ) T(n) = \sum_{i = 1}^{n}(n - i + 1) = \frac{n(n + 1)}{2} = O(n^2) T(n)=∑i=1n(n−i+1)=2n(n+1)=O(n2) |
五、选择排序的特性
选择排序具有以下特性:
- 不稳定性:在选择排序中,相同元素的相对位置可能会发生变化,导致算法是不稳定的。例如,考虑数组 [ 5 , 2 , 5 , 1 ] [5, 2, 5, 1] [5,2,5,1],第一个 5 5 5 和 1 1 1 会交换位置,导致第一个 5 5 5 与第二个 5 5 5 的相对位置改变。
- 简单直观:选择排序是一种简单直观的排序算法,易于理解和实现。它的核心思想是每次从待排序的元素中选择最小(或最大)的元素,将其放到已排序序列的末尾。
- 时间复杂度:选择排序的时间复杂度为 O ( n 2 ) O(n^2) O(n2),其中 n n n 是数组的长度。这是因为它包含了两层嵌套的循环,每次内层循环都要遍历剩余未排序的部分来寻找最小值。
- 空间复杂度:选择排序的空间复杂度为 O ( 1 ) O(1) O(1),因为它只需要常数级别的额外空间来存储临时变量和进行元素交换。
- 适用性:尽管选择排序通常不是最有效的排序算法,但在某些特定情况下,它可能是一个不错的选择。例如,对小型数组或者已经基本有序的数组进行排序时,选择排序的性能可能比较好。
- 不需要额外的空间:选择排序是一种原地排序算法,不需要额外的空间来存储临时数据。这意味着它在空间上的开销比较小,适用于内存受限的环境。
推荐阅读
- Spring 三级缓存
- 深入了解 MyBatis 插件:定制化你的持久层框架
- Zookeeper 注册中心:单机部署
- 【JavaScript】探索 JavaScript 中的解构赋值
- 深入理解 JavaScript 中的 Promise、async 和 await