如何理解与学习数学分析——第二部分——数学分析中的基本概念——第10章—

第2 部分：数学分析中的基本概念

(Concepts in Analysis)

10. 实数(The Real Numbers)

本章介绍比率数(rational numbers)和非比数(irrational numbers)及其与十进制展开的关系。讨论了实数的公理，并解释了完备性公理对于区分实数和比率数为何必不可少，并证明关于序列和函数的直观而令人信服的结果。

10.1 数的秘密(Things you don’t know about numbers)

你对数字解颇多。你可能会认为高等数学根本不是关于数的，而是关于一般公式和抽象关系的。在某种程度上，这是事实。然而，大多数本科数学学位都涉及对数论的深入研究。有些可能在一门叫做数论的课程中，这门课程(至少一开始)通常是关于整数的整除性质。你知道吗(例如)，对于一个整数，当且仅当其数字之和能被3 整除时，它能被 3 整除吗？如果你知道这一点，你知道为什么这是真的吗？这种事情很可爱，但并不是毫无意义的好奇心；它是由于十进制数字系统的基本属性而出现的。学习这种现象将把你的知识“向上”扩展，正如第 3.3 节所讨论的那样。像往常一样，分析是关于“向下”方向的——关于实数数学底层的理论。

作为一个初涉者，这里有一个用两种方式表示的数：

1/7 = 0.142857142857142857 . . .

请注意，小数表示是重复的(或循环的)。这是巧合吗？还有哪些数具有此属性？

每个人都认为小数是一数的天然表示方式，尤其是因为它们在计算器屏幕上就是那样的。知道如何使用计算器是件好事(我不是随便说说的——人们不这样做就会犯很多错误)，但在分析课上你不需要它。事实上，当学生在课堂上拿起计算器时，我就会把计算器拿走。部分原因是因为聪明的心算通常更快。部分原因是拥有数学上成熟的数的观念意味着的意义。例如，我最近出了一道考题，其中一个问题的答案是 $\frac{1}{6}(e-1)$ 。很多学生求得了这个答案，但又掏出计算器计算，并给出了一个诸如 0.28638030 这样的答案。然而，那些更理性的(nous)学生保留 $\frac{1}{6}(e-1)$ 为答案(注：“nous”是恐英式英语单词，发音类似“house”，我的计算机词典将其定义为“常识，实用智慧(common sense; practical intelligence)”)。这是数学家想要的。因为 $\frac{1}{6}(e-1)$ 是一个相当好的数。事实上，无论给出多少位小数，小数版本的准确性都较低。

但我主要还是会去掉计算器，因为分析并不是真正地将单个数作为答案，而是关于数背后的结构。计算器必然会掩盖这些结构——你得到了一个答案，但你不知道为什么它是正确的。在计算器上按下“1 ÷ 7 =”按钮将返回前八位或十位数字，这可能不足以显示重复的模式。使用计算机代数系统将提供更多数字，并可能突出显示模式，但它无法解释为什么会出现这种模式。在高等数学中，我们感兴趣的是为什么，在这种情况下，解释是相当容易理解的。

10.2 小数展开和比率数(Decimal expansions and rational numbers)

1/7 这个数有循环小数展开式并非巧合。这是因为 1/7 是比率数(rational number)。所有比率数的集合用 ℚ表示，以下是相应的定义：

定义：对于实数 x ，当且仅当 ∃ p ，q ∈ ℤ (q ≠ 0) 使得 x = p / q 时，x 是比率数。

通俗地讲，当且仅当 x 可以写成“分数”时(即整数比时)，它才是比率数。这样想是可以的，但要小心用词，因为人们倾向于认为分数“小”，而定义并没有明确这一点。例如，32800/7 是一个完美的比率数。它也有重复展开式，请看：

32800/7 = 4685.714285714285714285 . . .

事实上，扩展不仅重复，而且重复的周期与 1/7 的扩展周期相同：每六位数字重复一次。事实上，重复的数字是相同的，顺序也相同。如果这是巧合，那就太奇怪了。那么为什么会发生这种情况呢？

做长除法可以回答这个问题。我不知道现在的学校老师在描述长除法时会说什么，但我学会了这种不优雅但简短的措辞：

译注：

Seven into one doesn’t go. —— 7 除 1 ，商为 0 。“into”为前置词，词义为“除”。

Seven into ten goes one remainder three.——7 除 10 ，商为 1 ，余3。

Seven into thirty goes four remainder two.——7 除 30 ，商为 4 ，余2。

Seven into twenty goes two remainder six.——7 除 20 ，商为 2 ，余6。

Seven into sixty goes eight remainder four.——7 除 60 ，商为 8 ，余4。

Seven into fifty goes two remainder one.——7 除 15 ，商为 2 ，余1。

这个模式会在这个阶段重复，因为除法过程开始循环相同的余数集。事实上，这必然会发生，因为当除以 7 时，只有六个可能的非零余数。因此，在数字开始重复之前，最多会出现六个余数。这个观察结果很容易推广：当除以 q ∈ ℕ 时，最多有 q – 1 个可能的非零余数，因此数必须以最多 q – 1 的周期重复。

但这并不意味着周期一定恰好是 q – 1 。例如，

8/11 = 0.72727272 . . . 和 2/3 = 0.66666666 . . . 。

有些比率数在超过某个点后余数为零。例如，

7/8 = 0.8750000 . . . , 我们记为 7/8 = 0.875 。

但它确实意味着每个比率数都有一个循环或终止小数展开式。我认为这是一件不平凡的事情，而且解释如此简单也很好。不过，我们可以进一步提出本书中反复出现的问题：反之亦然吗？每个循环小数展开式都代表一个比率数吗？

答案也是肯定的。也许最简单的方法是使用一个特定的数并应用类似于第 6.4 节中用于等比级数的论证来理解原因。

令 x = 57.257257257257 . . . 。

则 1000x = 57257.257257257257 . . . 。

则 1000x – x = 57200,

即 999x = 57200 。

因此， $x =\frac{57200}{999 }$ 。

这个论点可以适用于处理任何循环小数扩展(如何？)(注：第 6.1 节中讨论的潜在问题在这种情况下不会造成麻烦。要了解原因，请参阅第 6.3 节并注意 $x = \frac{572}{10}( 1 + \frac{1}{10^{3}} + \frac{1}{10^{6}}+... )$ 。

所以比率数恰好是那些具有循环小数扩展的数。这更加不平凡——它说明了数属性与其表示之间的关系的一些基本知识。我认为很遗憾人们没有早点学习它，因为理解它所需的数相当简单。但你明白我的意思，还有很多东西要学。

说到小数，我们应该理清每个本科数学学生都应该知道的事情。它如下：

0.99999999 . . . = 1 。

这往往会让人感到不安。他们的直觉告诉他们，0.99999999... 比 1 小一点点，因为他们想象着写下这个数字，所以 9 会在一个“永无止境”的过程中被添加，而写下的数字“永远不会达到 1”。当然，这是完全合理的：像 0.99999999 这样的数字确实比 1 略小。但它只有有限多位数字。当数学家写下“0.99999999... ”或 “ $0.\dot{9}$ ”时，他们并没有想象写下 9 的过程。这些符号意味着无限多的 9 已经存在。那么 0.99999999... 和 1 之间有什么区别呢？它一定是零，这意味着数相等。

不过，最初的直觉是持久的，所以这里还有几种方法可以打败它。喜欢代数的人可能会喜欢这个：

令 x = 0.99999999 . . . 。

则 10x = 0.99999999 . . . 。

因此 10x – x = 9 ,

即 9x = 9 。

因此， $x = \frac{9}{9} = 1$ 。

或者更简单的算术怎么样？每个人都相信

1/3 = 0.33333333 . . . 。

现在只需将两边乘以 3。

这些都不是技巧。只是很多直觉都是基于有限对象的经验，这意味着当人们开始思考无限对象时，事情就会出错——在这种情况下是无限小数展开。事实上，这些思想可以与无限序列的极限相关，因为小数展开可以视为是每个项比上一项多包含一个额外数字的序列的极限：例如，序列 0.9、0.99、0.999、0.9999……的极限为 1。分析课程在探索序列和实数之间的联系方面有所不同，但您很可能会看到这些想法的延伸。

10.3 比率数和非比数(Rational and irrational numbers)

这里我们来对比一下比率数和非比数。比率数有很多，这就引出了一个问题：是否有可能把每个数都写成 p / q的形式。毕竟，p 和 q 的组合非常多。

然而，再想想小数展开，情况就开始变得不同了。所有比率数都可以表示为循环小数，显然有许多不循环的小数展开。很容易想象取一个循环小数展开，然后以多种方式“弄乱”它，以得到不循环的展开(简单但并不简单——我们需要把它弄得足够乱)。因此，小数展开的思想提供了洞察力，但它使非比数很难掌握：要完全表达一个非比数，我们必须写下无数个数字，但没有人能做到这一点。

但是，使用间接方法证明某些熟悉的数字是非比数并不难。粗略地说，当我们不直接证明某事为真，而是间接证明某事不能不为真时，就会使用“间接”一词。这听起来不太优雅，但实际上它可以得出一些相当漂亮的证明。一个经典的证明是使用矛盾法证明 $\sqrt{2}$ 是非比数，这里展示了它的一个版本。要理解这个证明，您需要知道符号 2|p 读作“2 除 p”，这意味着 2 是 p 的一个因数。还要注意，在这样的证明中，确保符号“|”和“/”是可区分的，这一点很重要。

断言： $\sqrt{2}$ 是非比数。

证明：使用反证法，假设 $\sqrt{2} \in \mathbb{Q}$ 。

则 ∃ p ，q ∈ ℤ (q ≠ 0) 使得 $\sqrt{2}= p/q$ 且p 和 q 没有公因子。这意味着 $2 = p^{2}/q^{2}$ ，因此 $2q^{2} = p^{2}$ 。因此， $2|p^{2}$ 。然而接着有2|p ，因为 2 是素数。比如，p = 2k ( k∈ℤ) 。

则 $2q^{2} = 4k^{2}$ ，因此， $q^{2} = 2k^{2}$ 。因此， $2|q^{2}$ 。然而接着有2|p ，因为 2 是素数。因此，p 和 q 有公因子 2 。但这与假设矛盾。因此， $\sqrt{2} \notin \mathbb{Q}$ 。

对于其他什么数，这样的证明是有效的？我们能用 $\sqrt{3}$ 代替 2 并仍然得到有效的论证吗？显然我们不能用 $\sqrt{4}$ 代替它，因为 $\sqrt{4}$ 不是非比数。但是证明会在哪一步失败？是否有多个步骤不适用于 $\sqrt{4}$ ，或者只有一个关键步骤无效？我们能用 $\sqrt{6}$ 代替 $\sqrt{2}$ 吗？如果是这样，还需要改变什么？像往常一样，你应该养成问自己这些问题的习惯。请注意，并非所有非比数都以平方根的形式出现。事实上，从某种重要意义上讲，非比数比比率数“多”得多——请留意这一点的证明。

像往常一样，典型的分析课程将介绍比率数和非比数，然后研究它们如何组合。例如，将两个比率数相乘总是会得到另一个比率数。为什么呢？将两个非比数相乘总是会得到一个非比数吗？这里要小心——答案是“不”，老师喜欢问这样的问题，以确保学生仔细思考。将比率数乘以非比数会怎样？这又会让人困惑，因为零是比率数，任何数乘以零都会得到零。但是，如果比率数不是零，我们就会得到另一个非比数。这也可以通过矛盾来证明，如下所示。

断言：若 x ∈ ℚ ，x ≠ 0 和 y ∉ ℚ ，则 xy ∉ ℚ 。

证明：令 x ∈ ℚ 且 x ≠ 0 。

则 ∃ p ，q ∈ ℤ (q ≠ 0) 使得 x = p/q 且p ≠ 0 ，因为 x ≠ 0 。

令 y ∉ ℚ ，使用反证法，假设 xy ∈ ℚ 。这意味着 ∃ r ，s ∈ ℤ (s ≠ 0) 使得 xy = r/s 。然而，接着有 $\displaystyle y =\frac{q}{p}\times \frac{r}{s} = \frac{qr}{ps}$ 。现在，qr ∈ ℤ 且 ps ∈ ℤ ，因为 p ， q ， r ， s ∈ ℤ 。此外，ps ≠ 0 ，因为 p ≠ 0且 s ≠ 0 。因此，y ∈ ℚ 。但这与定理的前提。因此，xy ∉ ℚ 。

矛盾证明在非比数的工作中经常出现，正是因为直接处理非比数很困难。实际上，人们的想法是，“我知道这个数是非比数，但比率数更容易处理，所以让我们假设它是比率数，并证明出了问题”。这正是矛盾证明的工作原理。

我们已经确定一些实数是比率数，一些是非比数。但很多事情对于所有实数都是正确的，这些公理就是本节的主题。

回想一下，我在第 2.2 节中列出了这些公理：

∀a, b ∈ ℝ , a + b = b + a [加法交换律(commutativity of addition)]；

∃ 0 ∈ ℝ 使得 ∀a ∈ ℝ, a + 0 = a = 0 + a [加法幺元存在性(existence of an additive identity)]。

您无疑相信这些公理是正确的。其他人也一样。但我们怎么知道呢？从哲学角度来看，答案很有趣，我们不知道。并不是说有人检查过每对可能的实数 a 和 b，以确保 a + b = b + a 确实总是正确的。从哲学角度来看，Plato主义者(Platonists)认为实数是存在的，像这样的公理是人类试图体现它们的一个属性。形式主义者认为，像这样的公理是规定集合属性的定义，我们可以选择将其称为实数；对于形式主义者来说，2 + 3 = 3 + 2 是正确的，因为公理是这么说的。这不是问题，根据你的学位结构，你可能会选修一门课程，该课程构建满足自然数、整数、比率数和实数的预期公理的集合。对于这样的书来说，这可能太详细了，但开始思考即使是简单的数学背后的哲学假设也是很好的。

无论如何，这些只是两个公理，而实数满足的条件要多得多；下面您可以找到一个列表。其中一些公理有名字，这些也列出了。你认为哪个名字与哪个公理相符？(这不是一个不合理的问题——根据你已经知道的知识，你将能够正确回答其中的大部分。)

公理：

(1) ∀a ，b ∈ ℝ，a + b ∈ ℝ 。

(2) ∀a ，b ∈ ℝ，ab ∈ ℝ 。

(3) ∀ a ，b ，c ∈ ℝ，(a + b) + c = a + (b + c)。

(4) ∀ a ，b ∈ ℝ， a + b = b + a 。

(5) ∃ 0 ∈ ℝ ，使得 ∀ a ∈ ℝ ，a + 0 = a = 0 + a 。

(6) ∀ a ∈ ℝ ∃ (–a) ∈ ℝ 使得 a + (-a) = 0 = (-a) + a 。

(7) ∀a，b， c ∈ ℝ， (ab)c = a(bc)。

(8) ∀a, b ∈ ℝ，ab = ba 。

(9) ∃ 1 ∈ ℝ 使得 ∀ a, b ∈ ℝ，a · 1 = a = 1 · a。

(10) ∀ a ∈ ℝ \{0} ∃ a-1b ∈ ℝ，使得 aa-1 = 1 = a-1 a。

(11) ∀ a，b， c∈ ℝ, a (b + c) = ab + ac。

(12) ∀ a, b∈ ℝ, 恰有 a < b, a = b 和 a > b 之一成立。

(13) ∀ a，b， c∈ ℝ, 若 a < b 和 b < c 则a < c。

(14) ∀ a，b， c ∈ ℝ, 若a < b 则a + c < b + c。

(15) ∀ a，b， c ∈ ℝ, 若a < b 和c > 0 则ca < c b。

公理名：

乘法下的闭包(closure under multiplication)

乘法结合律(associativity of multiplication)

乘法幺元存在性(existence of a multiplicative identity)

三分法(trichotomy)

加法交换律(commutativity of addition)

乘法逆元存在性(existence of multiplicative inverses)

加法下的闭包(closure under addition)

乘法交换律(commutativity of multiplication)

加法逆元存在性(existence of additive inverses)

传递性(transitivity)

乘法在加法之上的分配律(distributivity of multiplication over addition)

加法幺元存在性(existence of an additive identity)

公理的名字有点长，学生通常学不会。从某种意义上讲，这并不重要——你可以在不知道公理名字的情况下使用它。但名字对于识别跨学科的联系和有效的沟通都很有用。例如，加法和乘法都是可交换的——它们共享这个属性，所以用一个词来描述它是很有用的。数学家还研究复数、函数、矩阵、对称性、向量等等——其中许多对象可以相加或相乘，我们可以问加法和乘法是否保持交换性。此外，公理的受限集定义了诸如向量空间、群、环和域之类的结构，这些结构在基于线性代数和抽象代数的工作中被研究。命名公理使得比较和交流这些结构变得更容易。

不过，回到实数，这里有一个问题。在哪条公理中，我们可以用 ℚ 代替 ℝ？回顾并决定。

10.5 实数的完备性(Completeness)

上述问题的答案是“全部”：如果我们用 ℚ 替换 ℝ，所有十五条公理仍然适用。确保你相信这一点。因此，这一长串公理不足以区分实数和比率数。我们需要其他东西，而这种东西被称为完备性(completeness)。

完备性不是一个复杂的概念，但要理解它，您需要理解集合 X ⊆ ℝ 的上确界(supremum)的概念。

定义：对于 U∈ℝ 和 X ⊆ ℝ ，当且仅当

(1) 对 ∀ x∈X , x ≤U 和

(2) 若 u 是 X 的任意上界，则 U ≤ u 时，

我们称 U 是 X ⊆ ℝ的上确界。

有时，上确界被称为最小上界(the least upper bound)。你能明白为什么吗？定义中的第 1 点表示 U 是 X 的上界(参见第 2.6 节)，第 2 点表示它是所有可能上界中最小的一个。学生经常进一步采用非正式思维，假设集合的上确界是其最大或最大元素。不幸的是，这并不正确，因为并非每个集合都有最大元素。有些集合有：集合 [1, 5] = {x ∈ ℝ |1 ≤ x ≤ 5} 的最大元素为 5，5 也是其上确界(对照定义验证)。但集合 (1, 5) = { x ∈ ℝ |1 < x < 5} 没有最大元素：无论我们选择哪个 x ∈ (1, 5)，都会有一个更大的元素。不过，集合 (1, 5) 仍然有上确界，其上确界也是 5(再次验证)。5 恰好不在 (1, 5) 中。因此，注意定义并避免受到相关非正式想法的影响非常重要。不能避免受到左右的学生经常发现很难构建涉及上确界的证明，(注：如第 9.7 节所述，“supremum” 是单数，“suprema” 是复数——这就像 “maximum” 和 “maxima”。) 这并不是因为定义在逻辑上很复杂，而是因为他们认为自己理解了这个概念，所以他们不会想到要援引它。

类似的评论也适用于集合的下确界(infimum?)(也称为最大下界(the greatest lower bound))的定义。你能构造最小值的定义吗？为什么我们应该避免假设集合的最小值是其最小元素？

完备性公理：ℝ 中每一个有界的非空子集在 ℝ 中都有一个上确界。

完备性公理抓住了实数和比率数之间的区别；在这个公理中用 ℚ 代替 ℝ 会给出一个不正确的陈述。例如，集合 $\{x\in \mathbb{Q} | x^{2} < 2 \}$ 在 ℚ 中没有上确界；它的上确界是 $\sqrt{2}$ ，它在 ℝ 中但不在 ℚ 中——如果我们生活在一个只有比率数的世界里，并且我们放大数字线，我们会发现 $\sqrt{2}$ 应该在的地方有一个缺口。因此，人们有时会非正式地描述完备性公理，称 “在数轴(number line)上没有洞。”

这并不会让任何人感到惊讶，因为每个人都一直认为数轴上没有洞。但是，分析再次强调了我们所有人不假思索就做出的哲学假设。我们想假设数轴上没有洞，因此为了正确地公理化数的系统，我们需要明确地陈述这一点。

关注完备性可以更深入地理解其他分析主题的结果。例如，还记得第 5.4 节中的这个潜在定理吗？

• 每个有界单调序列都是收敛的。

这一点是正确的，对于大多数人来说，这在直觉上似乎是合理的：比如说，如果一个序列 $(a_{n})$ 是递增的，并且以 u 为界，那么无穷多个一定“融入(fit in)” $a_{1}$ 和 u 之间。事实上，极限将是所有序列项集合 $\{a_n|n \in \mathbb{N} \}$ 的上确界 U。请注意，该序列可能有或可能没有等于其极限的项，并且相应地，U 可能在或可能不在 $\{a_n|n \in \mathbb{N} \}$ 中。

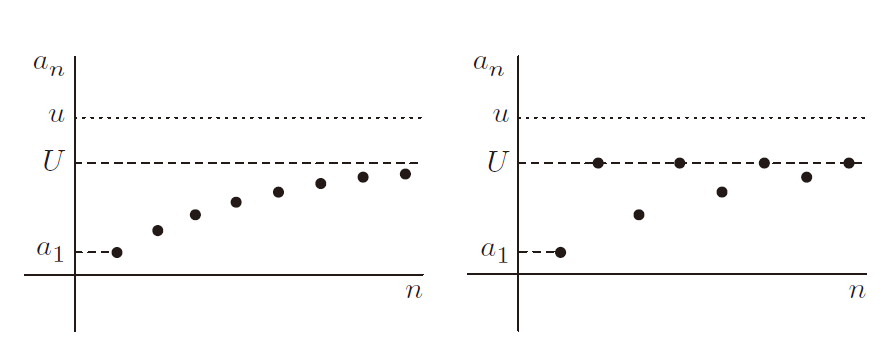
无论如何，这个定理只有在 ℝ 是完备的的情况下才成立。如果不是完备的，一些看似收敛的序列就不会有极限。例如，考虑第 n 项是 $\sqrt{3}$ 的 n 位小数近似值的序列：序列 1.7、1.73、1.732……如果我们生活在一个只有比率数的世界里，这个序列就会存在(每个项都是比率的——例如 1.732 = 1732/1000），但它的极限不存在。同样，考虑第 7.9 节中的这个定理：

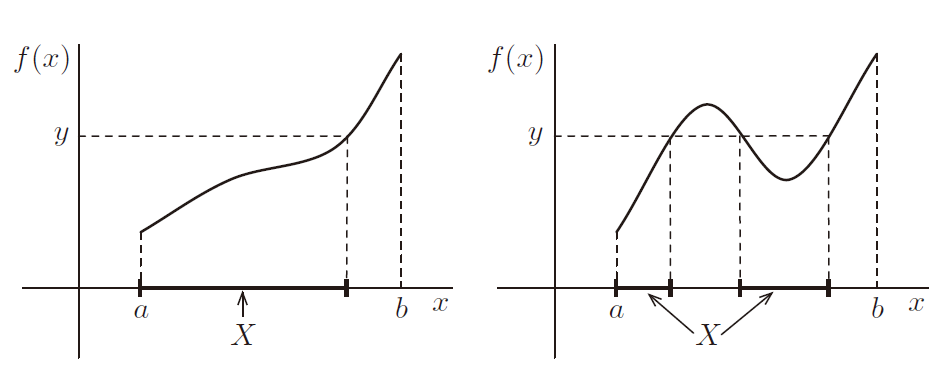
介值定理 (Intermediate Value Theorem): 若函数 f 在闭区间[a，b]上连续，且 y 介于 f (a)和 f (b)之间。则 ∃c ∈ (a，b) ,使得 f (c) = y 。

这也是正确的，我们需要完备性来证明这一点。如果实数不完备，那么函数图像就会有“洞”，并且可能存在没有适当 c 的值 y。典型的证明涉及考虑集合 X = {x ∈ [a, b]|f (x) < y}；这是 ℝ 的有界子集，因此根据完备性公理，它一定在 ℝ 中有一个上确界 c，并且 f (c) = y 一定成立。细节需要充实，但思考下面的图像可能会帮助您理解证明——在每种情况下， $c=\sup {X}$ 在哪里？

10.6 前瞻(Look ahead)

本章介绍了您在分析中可能会遇到的有关实数的概念。根据您的学位课程，您可能不会超出这个范围——如果您主要从事应用数学，那么您的研究将依赖于数的属性，但公理和定义将保留在背景中。但是，如果您做更多的纯数学，这些思想将在多个方向上得到扩展。

你可能会研究的一件事是，根据数作为不同类型方程的解的状态对数进行分类。例如，比率数是“好”的，因为它们是线性方程的解，如 3x – 4 = 0。非比数就没那么好，因为它们不是，但有些是二次方程的解，如 $x^{2}-2=0$ 。一般来说，如果一个数是具有整系数的形式为 $a_{n} x^{n} + . . . + a_{2} x^{2}+ a_{1}x + a_{0} = 0$ 的方程的解，则称它是代数的。然而，有些非比数甚至没有那么好。例如，e 和 π 都是超越数(transcendental)，这意味着它们不满足任何这样的方程；你可能会看到这一点被证明。你还可以研究代数方程解集的性质——被称为Galois理论的学科是关于由此类解形成的抽象群结构，它在几何学和抽象代数中都有着深远的影响。

您可能要进一步了解的另一件事是公理系统。正如我所提到的，向量空间、群、环和域等结构都是由第 10.4 节中列出的公理的子集定义的；大多数数学学生都会研究这些结构的具体示例和有关其属性的一般定理。现在，您可能想考虑一下哪些熟悉的数学集合(ℕ、ℤ、ℚ、ℂ(所有复数的集合)、所有三分量向量的集合、所有 2 × 2 矩阵的集合等等)满足哪些条件。请注意，某些公理在某些结构中不成立——例如，ℤ 具有加法逆元但没有乘法逆元。有些公理可能根本不适用：顺序公理(关于不等式的公理)对复数或矩阵毫无意义——说一个矩阵“小于”另一个矩阵意味着什么？这意味着这些系统中所能进行的数学类型以及所应用的定理和理论存在根本差异。

最后，你可以选修一门基础课程。这门课程可能会用等价关系来描述比率数，阐明 $\frac{1}{2}=\frac{2}{4}=\frac{3}{6}=...$ 的含义，并证明比率数的所有代数性质都符合这些关系。或者，它可能会追溯得更远，使用集合论来构造自然数、整数、比率数和实数。这类课程要求学生停止将他们的基本数学知识视为理所当然，因此它们具有挑战性，但它们触及了数学的核心。