堆

·定义
·基本操作
·建堆
·堆排序
·优先队列

一、堆的定义：
·堆必须是一个完全二叉树
·还得满足堆序性

什么是完全二叉树呢？
·完全二叉树只允许最后一行不为满
·且最后一行必须从左到右排序
·最后一行元素之间不可有间隔，中间不可有空缺

如下几棵树是完全二叉树：

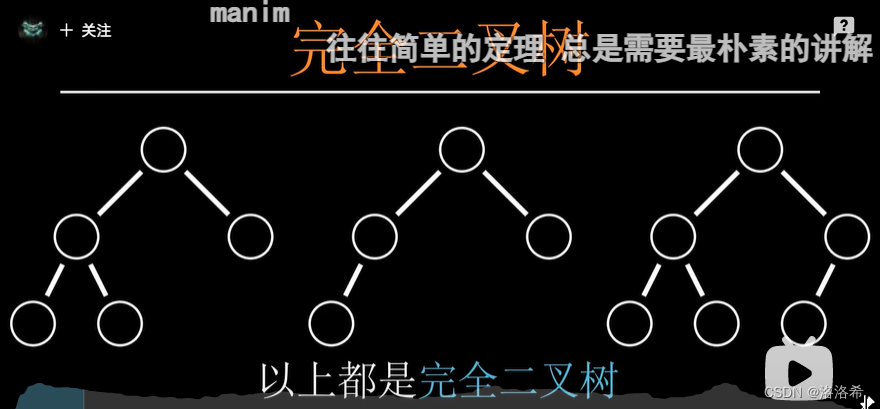
不是完全二叉树：

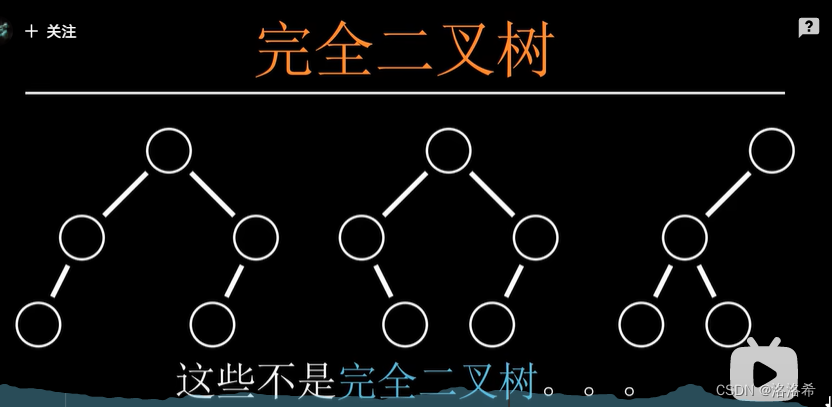
二、堆序性：
根据堆序性，可以把对分为两类：
·大根堆：每个父节点都大于它的子节点
·小根堆：每个父节点都小于它的子节点
节点下标为i，左节点为2i+1，右节点为2i+2

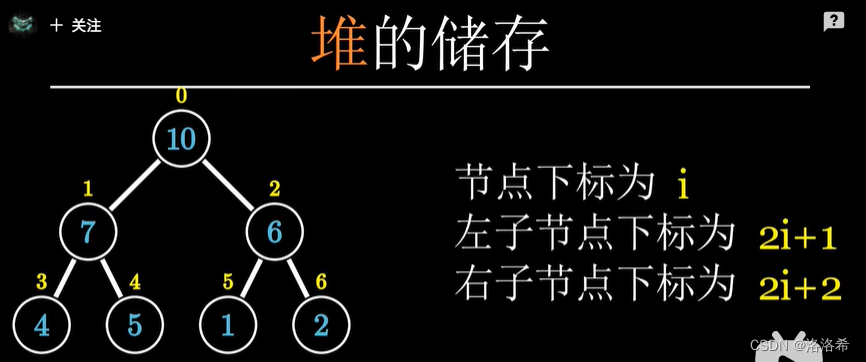
三、堆的基本操作
·上滤
·下滤
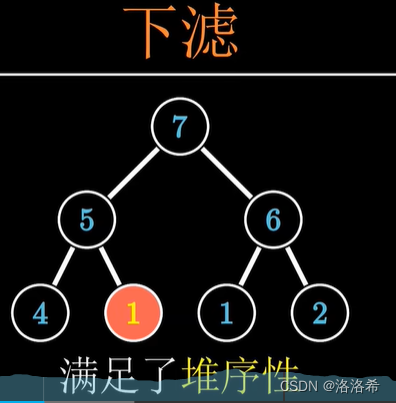
下滤：我们把根节点向下调整的方法叫做下滤。复杂度：O(logN)

以大根堆为例，我们将破坏堆序性的元素跟其他的最大子节点比较，如果小于它的最大子节点就与之交换，持续比较，交换，直到该元素大于它的子节点为止，或者移动到底部为止。

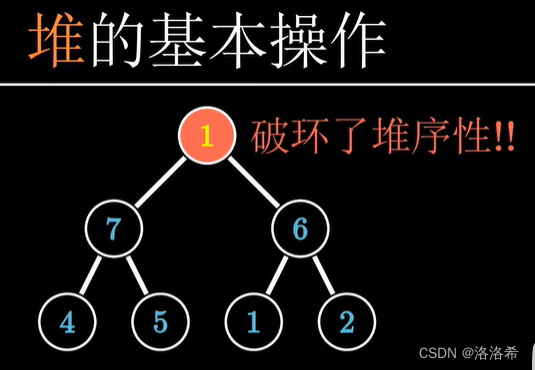
经过下滤：

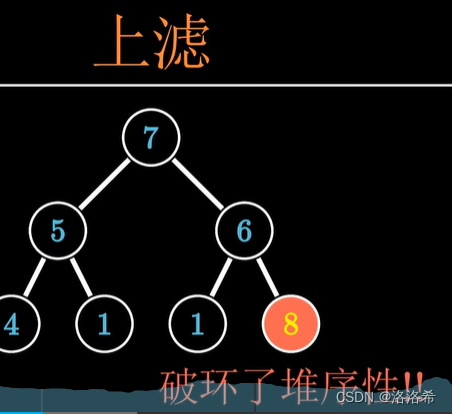
·上滤：我们把子节点向上调整的方法叫做上滤
这一次的情况是只有树的最后一个元素破坏了堆序性，同理让它和它的父元素进行过比较。复杂度为：O(logN)

经过上滤：

---

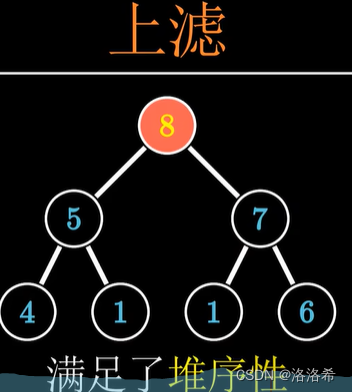
四、如果有一个乱序的数组，要怎么操作才能把它转化成堆呢？
建堆方法：
·自顶向下：对应的操作为上滤，步骤为：1.插入堆，2.上滤
–将新元素放在堆的最后一位，然后对其进行上滤操作。
复杂度为O(N logN)

·自下向上：从倒数第二层开始，对每个父节点进行下滤。复杂度为O(N)
思路：先把下面的元素调整成堆（根先不管），然后再对父节点进行下滤操作，具体操作是从倒数第二排开始。

---

五、应用：
1.优先队列：可以用小根堆实现，因为小根堆根元素就是最小元素
·插入队列：上滤操作本来就是插入堆的操作，复杂度O(logN)
·弹出最小元素，弹出后要把剩下的元素调整成堆，复杂度O(logN)，方法：
1、把最后一个元素放到根节点
2、进行下滤操作

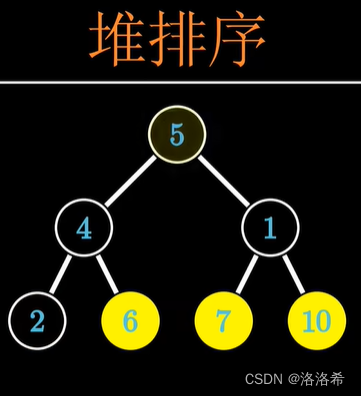
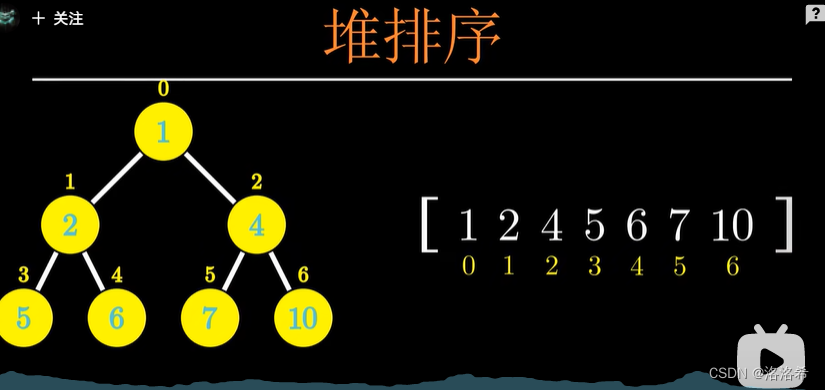
2.堆排序（复杂度O(N logN)）：
·存放的结果，会存放在堆的空节点里。
·我们使用大根堆进行从小到大的排序，使用小根堆进行从大到小的排序。

以大根堆从小到大排序为例：
步骤一：把根节点与最后一个没排序的节点进行交换
步骤二：寻找最大的根节点
重复步骤一二