文章目录
- 序言
- 1. 线性回归
- 2. 逻辑回归
- 2.1 引入逻辑回归的原因
- 2.2 逻辑回归
- 2.3 逻辑回归的应用
- 3. 逻辑函数
- 3.1 sigmoid函数
- 3.2 sigmoid函数的性质
- 3.3 决策边界
- 3.4 对数几率
- 4. 损失函数
- 4.1 为什么说逻辑回归时概率类模型
- 4.2 为什么要进行极大似然估计
- 4.3 利用MLE如何推导出损失函数
- 4.4 损失函数/代价函数/目标函数
- 5. 最优化问题
- 6. sigmoid和softmax
- 7. LR模型的性质和优缺点
- 7.1 逻辑回归与线性回归的联系与区别
- 7.2 逻辑回归的优缺点
- 8. LR模型实例
- 8.1 sklearn导入LR模型实现鸢尾花分类
- 8.2 单层线性网络实现LR的鸢尾花分类
- 9. 疑问厘清
序言
- 总结逻辑回归模型,LR模型实例
1. 线性回归
- 一元线性回归: y = a + b x y=a+bx y=a+bx
- 多元线性回归:
z
=
h
(
x
)
=
w
0
x
0
+
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
n
x
n
=
W
T
X
z = h(x) = w_{0}x_{0} + w_{1}x_{1}+ w_{2}x_{2} +...+w_{n}x_{n} = W^{T} X
z=h(x)=w0x0+w1x1+w2x2+...+wnxn=WTX
- 每个样本 n n n个特征,每个特征 x i x_{i} xi都有对应的权值 w i w_{i} wi
- x 0 = 1 x_{0} = 1 x0=1, w 0 w_{0} w0其实是偏置量,为了公式简洁和方便计算
- 不管是一元线性回归分析还是多元线性回归分析,都是线性回归分析
2. 逻辑回归
2.1 引入逻辑回归的原因
- 在一些特别的情况下, 线性回归可以用于分类问题, 找到分类的阈值, 但是一旦样本点出现分布不均匀, 会导致线性方程的参数产生偏移, 造成严重的误差
- 另一方面, 我们希望分类模型的输出是0,1即可, 线性回归的值域在 ( − ∞ , + ∞ ) (-\infty , +\infty ) (−∞,+∞), 是连续的, 不满足我们的要求
2.2 逻辑回归
- 逻辑回归与线性回归都是广义线性模型, 线性回归假设Y|X服从高斯分布, 逻辑回归假设Y|X服从伯努利分布
- 逻辑回归以线性回归为理论支持, 通过逻辑函数(Sigmoid函数)引入非线性因素。逻辑回归的思路就是将线性回归的结果z通过逻辑函数g(z)从 ( − ∞ , + ∞ ) (-\infty , +\infty ) (−∞,+∞)映射到(0,1), 再通过决策边界建立与分类的概率联系
- 逻辑回归虽然带有"回归"二字, 但却是一种分类模型, 最常见的是用于处理二分类问题
- 逻辑回归假设数据服从伯努利分布(二项分布,0-1分布),通过极大似然估计的方法,运用梯度下降法求解参数,来达到将数据二分类的目的
2.3 逻辑回归的应用
- 逻辑回归模型广泛用于各个领域,包括机器学习,大多数医学领域和社会科学
- 逻辑回归模型也用于预测在给定的过程中,系统或产品的故障的可能性
- 逻辑回归模型现在同样是很多分类算法的基础组件,其模型清晰有对应的概率学理论基础,是理解数据的好工具
3. 逻辑函数
3.1 sigmoid函数
g ( z ) = 1 1 + e − z g(z) = \frac{1}{1+e^{-z} } g(z)=1+e−z1
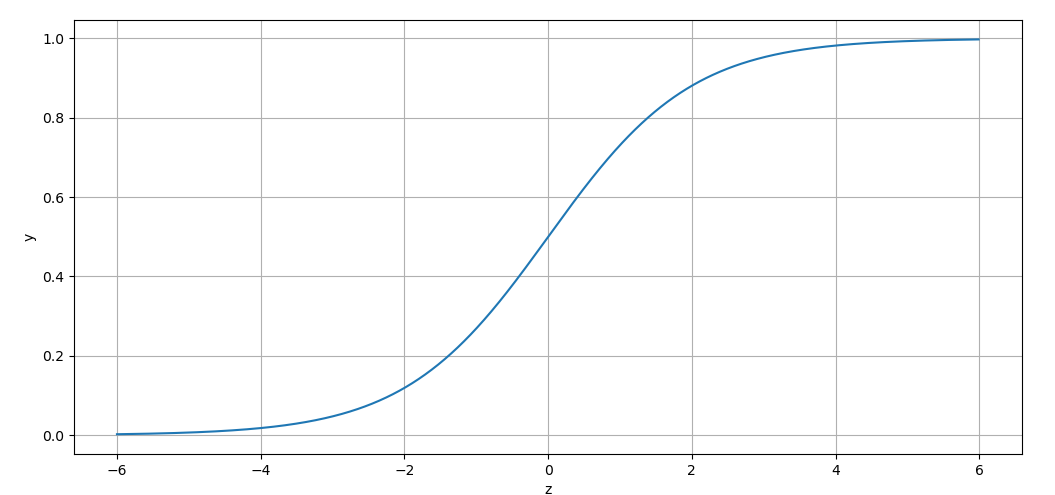
3.2 sigmoid函数的性质
- 任意输入压缩到0-1之间
- 任意阶可导, 函数在z = 0处的导数最大
- 函数满足关系: g ( − z ) = 1 − g ( z ) g(-z) = 1 - g(z) g(−z)=1−g(z)
- 导函数满足关系: ∂ g ( z ) ∂ z = g ( z ) ( 1 − g ( z ) ) \frac{\partial g(z)}{\partial z} = g(z)(1-g(z)) ∂z∂g(z)=g(z)(1−g(z))
- 函数两边梯度趋于饱和, 容易导致梯度消失
- z=5时,g(z)已经在0.99以上
3.3 决策边界
- 将线性回归结果带入g(z)函数, 得到0~1之间的概率值, 如果认为p > 0.5属于一类, 否则是另一类, 那么0.5就是决策边界
3.4 对数几率
- 逻辑函数做如下抓换
g ( z ) = 1 1 + e − z ⇒ g ( z ) ∗ ( 1 + e − z ) = 1 ⇒ e − z = 1 g ( z ) − 1 ⇒ − z = l n ( 1 − g ( z ) g ( z ) ) ⇒ z = l n ( g ( z ) 1 − g ( z ) ) g(z) = \frac{1}{1+e^{-z} } \Rightarrow g(z)*(1+e^{-z} )=1 \Rightarrow e^{-z} = \frac{1}{g(z)}-1 \Rightarrow -z=ln(\frac{1-g(z)}{g(z)} ) \Rightarrow z=ln(\frac{g(z)}{1-g(z)} ) g(z)=1+e−z1⇒g(z)∗(1+e−z)=1⇒e−z=g(z)1−1⇒−z=ln(g(z)1−g(z))⇒z=ln(1−g(z)g(z))
- 上式中, z = h ( x ) = θ T X = W T X z = h(x) = \theta ^{T} X = W^{T}X z=h(x)=θTX=WTX
- 如果将逻辑回归结果 g ( z ) g(z) g(z)看成某个事件发生的概率,事件不发生的概率就是 1 − g ( z ) 1 - g(z) 1−g(z),两者比值称之为几率odds
- 令 g ( z ) = p g(z)=p g(z)=p,得到如下公式
z = θ T X = l n ( g ( z ) 1 − g ( z ) ) = l n ( p 1 − p ) = l n ( 几率 ) = l n ( o d d s ) z = \theta ^{T} X=ln(\frac{g(z)}{1-g(z)})=ln(\frac{p}{1-p} )=ln(几率)=ln(odds) z=θTX=ln(1−g(z)g(z))=ln(1−pp)=ln(几率)=ln(odds)
- 也就是说,线性回归的结果(即 z = θ T X z=\theta ^{T} X z=θTX)等于对数几率。所以逻辑回归模型也叫对率回归模型
4. 损失函数
- 逻辑回归的假设有两个
- 假设数据服从伯努利分布
- 假设模型的输出值是样本为正例的概率
- 基于这两个假设,可以分别得到类别为正例1和反例0的后验概率估计:
p ( y = 1 ∣ x , θ ) = h θ ( x ) = 1 1 + e − x θ p(y=1|x,\theta )=h_{\theta } (x)=\frac{1}{1+e^{-x\theta } } p(y=1∣x,θ)=hθ(x)=1+e−xθ1
p ( y = 0 ∣ x , θ ) = 1 − h θ ( x ) = e − x θ 1 + e − x θ p(y=0|x,\theta )=1- h_{\theta } (x)=\frac{e^{-x\theta } }{1+e^{-x\theta } } p(y=0∣x,θ)=1−hθ(x)=1+e−xθe−xθ
4.1 为什么说逻辑回归时概率类模型
- 直接建模了目标变量0-1的条件概率, 如上, 通过逻辑函数sigmoid将线性回归模型的输出转换为概率值,从而预测给定输入特征下目标变量取某个值(0或1)的概率
- 在实际应用中, 可以根据逻辑回归模型输出的概率值来做出决策(决策边界)
- 逻辑回归输出的概率值有明确的概率解释
4.2 为什么要进行极大似然估计
- 首先模型训练的目的是找到最能描述观测到的结果的模型, 在逻辑回归中, 意味着找到一组参数, 使得在给定输入特征下, 模型预测的结果与观测到的结果最为接近
- 如果使用线性回归的损失函数如MSE等来评估模型的训练过程, 由于所得函数非凸, 而且有很多局部极小值, 不利于求解。如下图所示
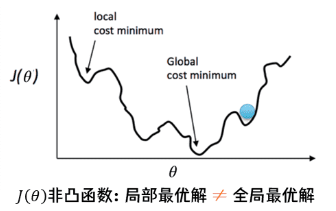
- 结合上面所述, 逻辑回归是概率模型, 可以通过似然估计来推导其损失函数
4.3 利用MLE如何推导出损失函数
- 逻辑回归的交叉熵损失函数是通过最大似然估计出来的
- 什么是极大似然估计
- 极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计
- (1)以上通过基本假设得到了1和0两类的后验概率,现在将两个概率合并可得到
p
(
y
∣
x
,
θ
)
=
h
θ
(
x
)
y
(
1
−
h
θ
(
x
)
)
1
−
y
,
y
∈
0
,
1
p(y|x,\theta )=h_{\theta }(x)^{y} (1-h_{\theta }(x))^{1-y} , y\in {0,1}
p(y∣x,θ)=hθ(x)y(1−hθ(x))1−y,y∈0,1
\qquad
\qquad
当
y
=
1
y = 1
y=1时,上式为类别1的后验概率;当
y
=
0
y = 0
y=0时,上式为类别0的后验概率
-
(2)我们假定样本数据都是独立同分布的(是逻辑回归的基本假设->联合分布可用乘法),使用极大似然估计来根据给定的训练数据集估计出模型参数,讲n个训练样本的概率相乘得到
L ( θ ) = ∏ i = 1 n p ( y ( i ) ∣ x ( i ) , θ ) = ∏ i = 1 n h θ ( x ( i ) ) y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − y ( i ) L(\theta )=\prod_{i=1}^{n} p(y^{(i)} |x^{(i)} ,\theta )=\prod_{i=1}^{n} h_{\theta }(x^{(i)} )^{y^{(i)} } (1-h_{\theta }(x^{(i)} ))^{1-y^{(i)} } L(θ)=i=1∏np(y(i)∣x(i),θ)=i=1∏nhθ(x(i))y(i)(1−hθ(x(i)))1−y(i) -
(3)似然函数是相乘的模型,可以通过取对数将右边变为相加的模型,然后将指数提前便于求解。变换后如下
l ( θ ) = l n ( L ( θ ) ) = ∑ i = 1 n y ( i ) l n [ h θ ( x ( i ) ) ] + ( 1 − y ( i ) ) l n [ 1 − h θ ( x ( i ) ) ] l(\theta )=ln(L(\theta ))=\sum_{i=1}^{n} y^{(i)}ln[h_{\theta }(x^{(i)} )] +(1-y^{(i)} )ln[1-h_{\theta }(x^{(i)} )] l(θ)=ln(L(θ))=i=1∑ny(i)ln[hθ(x(i))]+(1−y(i))ln[1−hθ(x(i))]
\qquad 引入不改变函数单调性的对数函数ln,把连乘变成加法。使用对数似然函数,不仅仅把连乘变成加法,便于求解,而且对数似然函数对应的损失函数是关于未知参数 θ \theta θ的高阶连续可导的凸函数,便于求解全局最优解 -
(4)如果取整个数据集上的平均对数似然损失,可以得到
J ( θ ) = − 1 n l ( θ ) = − 1 n l n ( L ( θ ) ) J(\theta )=-\frac{1}{n} l(\theta )=-\frac{1}{n} ln(L(\theta )) J(θ)=−n1l(θ)=−n1ln(L(θ))
\qquad 如上公式的 J ( θ ) J(\theta) J(θ)为对数损失函数(二元交叉损失熵),由对数似然函数添加负号取平均得到,即在逻辑回归模型中,最大化似然函数与最小化损失函数实际上是等价的,即求最大化似然函数的参数 θ \theta θ与求最小化平均对数似然损失函数对应的参数 θ \theta θ是一致的,那么有
max l n ( L ( θ ) ) ⇔ min J ( θ ) \max ln(L(\theta ))\Leftrightarrow \min J(\theta) maxln(L(θ))⇔minJ(θ)
\qquad 之所以要加负号,是因为机器学习的目标是最小化损失函数,而极大似然估计法的目标是最大化似然函数。加个负号,正好使二者等价 -
(5)我们将对数损失函数最小化,如此得到参数的最大似然估计。对数损失函数的公式:
J ( θ ) = − 1 n [ ∑ i = 1 n y ( i ) l n [ h θ ( x ( i ) ) ] + ( 1 − y ( i ) ) l n [ 1 − h θ ( x ( i ) ) ] ] J(\theta )=-\frac{1}{n} \left [ \sum_{i=1}^{n} y^{(i)}ln[h_{\theta }(x^{(i)} )] +(1-y^{(i)} )ln[1-h_{\theta }(x^{(i)} )] \right ] J(θ)=−n1[i=1∑ny(i)ln[hθ(x(i))]+(1−y(i))ln[1−hθ(x(i))]]
\qquad 其中 y ( i ) y^{(i)} y(i)表示样本取值,正样本时取值为1,负样本时取值为0。我们分两种情况来分析
C o s t ( h θ ( x ) , y ) = { − l n ( h θ ( x ) ) if y = 1 − l n ( 1 − h θ ( x ) ) if y = 0 Cost(h_{\theta }(x),y)=\begin{cases} -ln(h_{\theta }(x)) & \text{ if } y=1 \\ -ln(1-h_{\theta }(x)) & \text{ if } y=0 \end{cases} Cost(hθ(x),y)={−ln(hθ(x))−ln(1−hθ(x)) if y=1 if y=0
\qquad 当 y = 1 y = 1 y=1,正样本,若 h θ ( x ( i ) ) h_{\theta }(x^{(i)} ) hθ(x(i))结果接近0,即预测为负样本,那么 − l n ( h θ ( x ) ) -ln(h_{\theta }(x)) −ln(hθ(x))就会很大,如下图,损失就大得到的惩罚就大
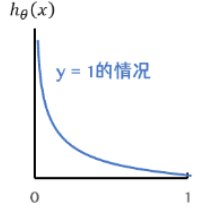
\qquad 当 y = 0 y = 0 y=0,负样本,若 h θ ( x ( i ) ) h_{\theta }(x^{(i)} ) hθ(x(i))结果接近1,即预测为正样本,那么 − l n ( 1 − h θ ( x ) ) -ln(1- h_{\theta }(x)) −ln(1−hθ(x))就会很大,如下图,损失就大得到的惩罚就大
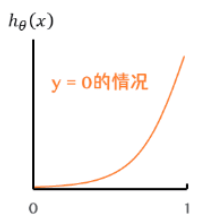
\qquad 这种惩罚的存在,模型会倾向于让预测输出更接近于真实样本标签 y y y
- (6)如何求得损失函数最小对应的参数呢,使用梯度下降法,损失函数对特征
j
j
j求偏导,
i
i
i表示样本

\qquad 至此,我们找到了梯度下降的方向,只要给定一个步长就可以用迭代的方式来求待求参数,迭代的公式为:
θ
j
(
k
+
1
)
=
θ
j
(
k
)
−
α
F
\theta _{j}^{(k+1)} =\theta _{j}^{(k)} -\alpha F
θj(k+1)=θj(k)−αF
\qquad
其中
α
\alpha
α为学习率,是一个大于零的数,控制沿着某个方向走多长一段距离,
F
F
F为下降方向
F
=
∂
J
(
θ
)
∂
θ
j
F=\frac{\partial J(\theta )}{\partial \theta _{j} }
F=∂θj∂J(θ)
\qquad
所以参数迭代公式可写为:
θ
j
(
k
+
1
)
=
θ
j
(
k
)
−
α
∗
1
n
∑
i
=
1
n
[
h
(
θ
T
x
(
i
)
)
−
y
(
i
)
]
∗
x
j
(
i
)
\theta _{j}^{(k+1)} =\theta _{j}^{(k)} -\alpha *\frac{1}{n} \sum_{i=1}^{n} [h(\theta ^{T}x^{(i)} )-y^{(i)}] *x_{j}^{(i)}
θj(k+1)=θj(k)−α∗n1i=1∑n[h(θTx(i))−y(i)]∗xj(i)
\qquad
当迭代到一定次数或学习曲线小于某个阈值时,停止迭代。
4.4 损失函数/代价函数/目标函数
- 损失函数:Loss Function,直接作用于单个样本,用来表达样本的误差
- 代价函数:Cost Function,整个样本集的平均误差,对所有损失函数的平均
- 经过上面公式的推导可知,一个好的代价函数需要满足两个基本的要求:能评价模型的准确性,对参数 θ \theta θ可微
- 目标函数:Object Function,是我们最终要优化的函数
5. 最优化问题
-
按照章节4中的推导,我们的目标就是最小化损失函数
m i n J ( θ ) = − 1 n [ ∑ i = 1 n y ( i ) l n [ h θ ( x ( i ) ) ] + ( 1 − y ( i ) ) l n [ 1 − h θ ( x ( i ) ) ] ] min J(\theta )=-\frac{1}{n} \left [ \sum_{i=1}^{n} y^{(i)}ln[h_{\theta }(x^{(i)} )] +(1-y^{(i)} )ln[1-h_{\theta }(x^{(i)} )] \right ] minJ(θ)=−n1[i=1∑ny(i)ln[hθ(x(i))]+(1−y(i))ln[1−hθ(x(i))]] -
通过梯度下降法求解,参数迭代公式
θ j ( k + 1 ) = θ j ( k ) − α ∗ 1 n ∑ i = 1 n [ h ( θ T x ( i ) ) − y ( i ) ] ∗ x j ( i ) \theta _{j}^{(k+1)} =\theta _{j}^{(k)} -\alpha *\frac{1}{n} \sum_{i=1}^{n} [h(\theta ^{T}x^{(i)} )-y^{(i)}] *x_{j}^{(i)} θj(k+1)=θj(k)−α∗n1i=1∑n[h(θTx(i))−y(i)]∗xj(i)
6. sigmoid和softmax
- sigmoid用于二分类问题
- softmax用于多分类问题, softmax函数的定义
s o f t m a x ( z i ) = e x p ( z i ) ∑ j = 1 K e x p ( z j ) , 1 ≤ i ≤ K softmax(z_{i} )=\frac{exp(z_{i} )}{ {\textstyle \sum_{j=1}^{K}}exp(z_{j} ) } ,1 \le i\le K softmax(zi)=∑j=1Kexp(zj)exp(zi),1≤i≤K - 与 sigmoid 一样,softmax 也具有将异常值压向 0 或 1 的特性
- 多分类问题使用softmax, 使用sigmoid通过One_vs_Rest为每个类别训练一个LR模型也能达成多分类目的
7. LR模型的性质和优缺点
7.1 逻辑回归与线性回归的联系与区别
-
区别
- 线性回归假设因变量(回归结果)服从正态分布,逻辑回归假设因变量(分类结果)服从伯努利分布(0-1分布,二项分布)
- 线性回归的损失函数是均方差MSE,而逻辑回归的损失函数是似然函数(最大化)/对数损失函数(最小化)
- 线性回归要求自变量和因变量呈线性关系,而逻辑回归没有要求
- 线性回归分析的是因变量与自变量的关系,逻辑回归无法表达变量之间的关系,辑回归研究的是因变量取值的概率与自变量的概率
- 线性回归处理的是回归问题,逻辑回归处理的是分类问题
- 线性回归要求自变量是连续数值变量,逻辑回归要求因变量是离散的变量
- 线性回归取值范围实数域,逻辑回归取值范围0-1
-
联系
- 两个都是线性模型。线性回归是普通线性模型,逻辑回归是广义线性模型
- 表达形式上,逻辑回归是线性回归的结果套上一个sigmoid函数
7.2 逻辑回归的优缺点
-
优点
- 无需假设数据分布,直接对分类的可能性建模,避免对数据分布假设不准确带来的问题
- 不仅能预测出类别,还能得到类别的概率,输出值在0-1之间,有概率意义
- 对率函数是任意阶可导的凸函数,可直接用于求解最优解
- 原理简单,模型清晰,操作高效,容易使用和解释,计算代价低,速度很快,存储资源低
- 可进行在线算法实现,用较小资源处理较大数据
- 对数据中小噪声鲁棒性好
- 结果是概率,可用作排序模型
- 求出来的参数代表每个特征对输出的影响,可解释性强
- 解决过拟合方法很多,如L1/L2正则化,L2正则化可以解决多重共线性问题
-
缺点
- 对数据依赖强,很多时候需要做特征工程
- 主要用来解决线性可分问题,对于非线性特征需要进行转换
- 由于它是一个线性的分类器,处理不好特征相关的情况。比如两个高度相关特征放入模型,可能导致较弱自变量的符号不符合预期,符号相反
- 从sigmoid函数也能看出,在两端的变化率微乎其微,导致很多区间的变量变化对目标概率的影响没有区分度,很难确定阈值
- 容易欠拟合,分类精度不高
- 数据特征有缺失或者特征空间很大时效果不好,不能很好处理大量多类特征或变量
8. LR模型实例
8.1 sklearn导入LR模型实现鸢尾花分类
-
代码
# 1. 导入包 import pandas as pd import matplotlib.pyplot as plt import seaborn as sns # 2. 导入数据 from sklearn.datasets import load_iris # sklearn中自带的iris数据 data = load_iris() #得到数据特征 iris_target = data.target #得到数据对应的标签 iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为DataFrame格式 # 3. 查看数据信息 iris_features.info() # 利用.info()查看数据的整体信息 iris_features.describe() # 对于特征进行一些统计描述 # 4. 数据可视化 iris_all = iris_features.copy() # 进行浅拷贝,防止对于原始数据的修改 iris_all['target'] = iris_target # 合并标签和特征信息 # 特征与标签组合的散点可视化 sns.pairplot(data=iris_all, diag_kind='hist', hue='target') plt.show() # 箱线图: 显示数据的中心和散布范围, 中位数和离群值 for col in iris_features.columns: sns.boxplot(x='target', y=col, saturation=0.5, palette='pastel', data=iris_all) plt.title(col) plt.show() # 5. 模型训练与预测 from sklearn.model_selection import train_test_split from sklearn import metrics from sklearn.linear_model import LogisticRegression # 从sklearn中导入逻辑回归模型 ## 选择其类别为0和1的样本(不包括类别为2的样本) iris_features_part = iris_features.iloc[:100] iris_target_part = iris_target[:100] ## 训练集:测试集 = 7:3 x_train, x_test, y_train, y_test = train_test_split(iris_features_part, iris_target_part, test_size=0.3, random_state=2020) ## 定义逻辑回归模型: lbfgs为算法内部定义的优化方法,类似optimizer clf = LogisticRegression(random_state=0, solver='lbfgs') clf.fit(x_train, y_train) ## 在训练集和测试集上分布利用训练好的模型进行预测 train_predict = clf.predict(x_train) test_predict = clf.predict(x_test) # 6. 模型评估 ## 利用accuracy【预测正确的样本数目占总预测样本数目的比例】评估模型效果 print('The train-accuracy of the Logistic Regression is:', metrics.accuracy_score(y_train, train_predict)) print('The test-accuracy of the Logistic Regression is:', metrics.accuracy_score(y_test, test_predict)) ## 查看混淆矩阵 confusion_matrix_result = metrics.confusion_matrix(test_predict, y_test) print('The confusion matrix result:\n', confusion_matrix_result) -
补充1:数据可视化
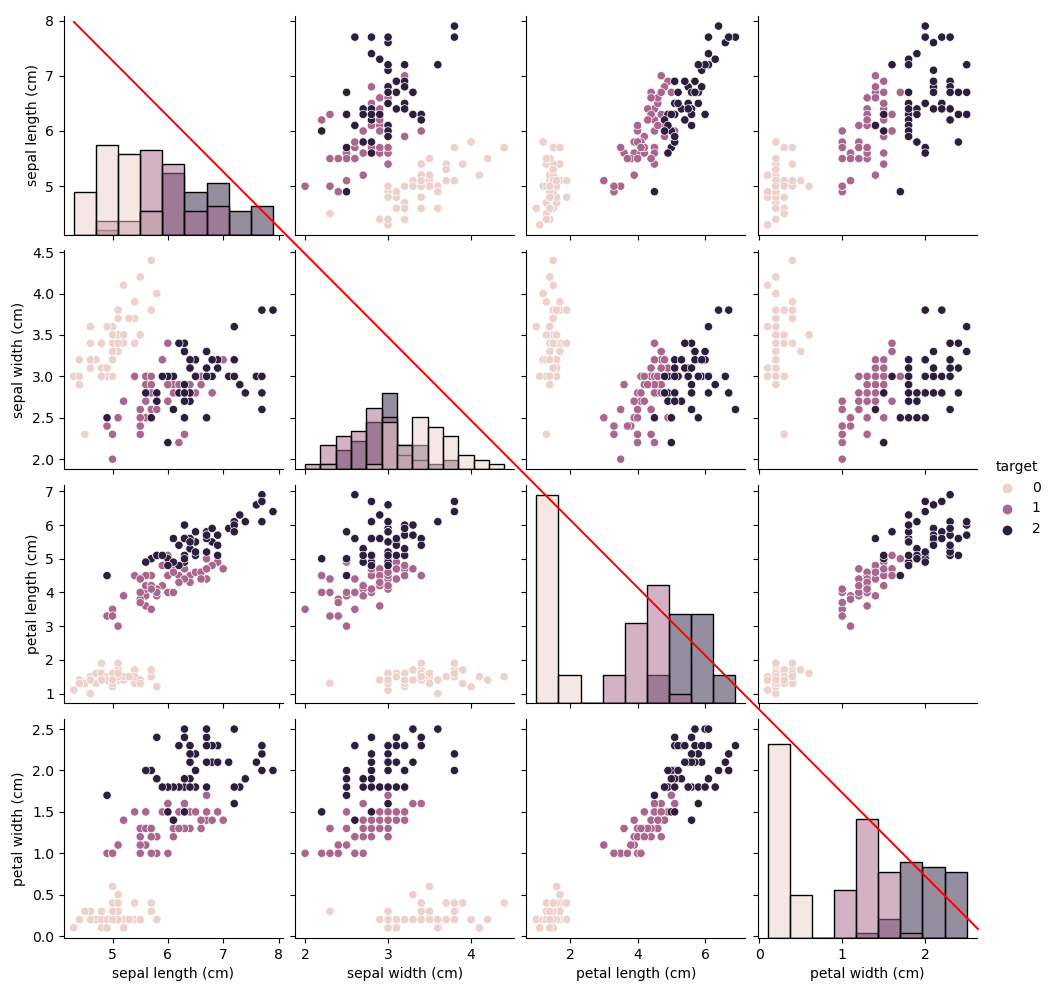
-
补充2:箱线图反映数据的分布, 中位数和离群值, 如sepal宽度的箱线图, 用于连续变量的数据分布. 点为离群值, 中心线偏上或偏下,表示数据分布是偏态的
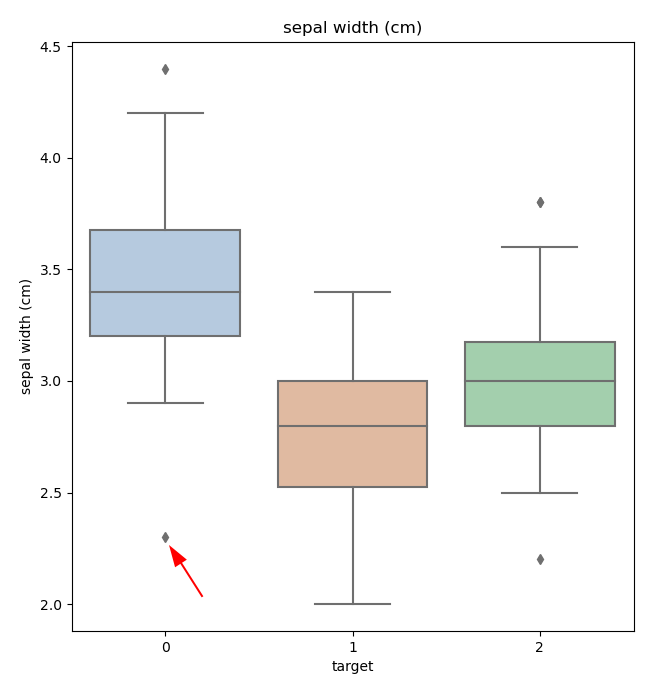
- 补充3:训练结果, 用acc来评估模型效果, 打印混淆矩阵
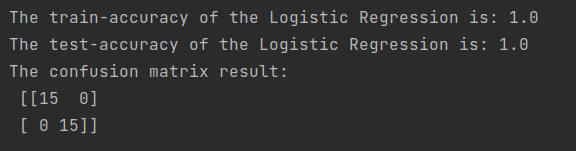
- 补充4:逻辑回归使用.fit方法而不是epochs来训练模型
- 使用.fit方法训练模型,这个方法会接收输入和输出矩阵,使用内部定义的优化方法来找到最佳参数,以最小化损失函数
- 不使用epochs进行训练,epoch是深度学习中的概念,传统机器学习中使用.fit来进行拟合
- 也就是说在神经网络中通常不会用单层线性网络Linear来实现逻辑回归, 因为逻辑回归本身就是一个简单的线性模型加上一个sigmoid激活函数来将输出映射到0~1之间, 可以被视为一个简单的神经网络
接下来就用单层线性网络加sigmoid激活函数来实现逻辑回归
8.2 单层线性网络实现LR的鸢尾花分类
-
代码
# 1. 导入包 import matplotlib.pyplot as plt import numpy as np from io import BytesIO import torch # 2. 数据集获取与划分 ds = np.lib.DataSource() fp = ds.open('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data') ## 从文本文件中加载数据,使用','做分隔符 x = np.genfromtxt(BytesIO(fp.read().encode()), delimiter=',', usecols=range(2), max_rows=100) y = np.zeros(100) y[50:] = 1 # 一半为1一半为0 ## 数据打乱后手动划分训练集和测试集7:3, 可以使用 sklearn.model_selection.train_test_split np.random.seed(1) idx = np.arange(y.shape[0]) np.random.shuffle(idx) X_test, y_test = x[idx[:30]], y[idx[:30]] X_train, y_train = x[idx[30:]], y[idx[30:]] ## 数据手动标准化, 可以使用sklearn.preprocessing.StandardScaler mu, std = np.mean(X_train, axis=0), np.std(X_train, axis=0) X_train, X_test = (X_train - mu) / std, (X_test - mu) / std # 3. 数据可视化 fig, ax = plt.subplots(1, 2, figsize=(7, 2.5)) ax[0].scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1]) ax[0].scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1]) ax[1].scatter(X_test[y_test == 1, 0], X_test[y_test == 1, 1]) ax[1].scatter(X_test[y_test == 0, 0], X_test[y_test == 0, 1]) plt.show() # 4. 模型定义 class LogisticRegression(torch.nn.Module): def __init__(self, num_features): super(LogisticRegression, self).__init__() # 调用父类的构造函数 self.linear = torch.nn.Linear(num_features, 1) # 输入维度num_features, 输出维度1 self.linear.weight.detach().zero_() # 权值 初始化为0 self.linear.bias.detach().zero_() # 偏置 初始化为0 def forward(self, x): logits = self.linear(x) prob = torch.sigmoid(logits) # 线性回归的输出经过sigmoid函数得到概率 return prob # 4. 模型初始化 device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') model = LogisticRegression(num_features=2).to(device) cost_fn = torch.nn.BCELoss(reduction='sum') optimizer = torch.optim.SGD(model.parameters(), lr=0.1) ## 概率值转换为label, 分类阈值为0.5 def prob_to_label(cond, x_1, x_2): return (cond * x_1) + ((1 - cond) * x_2) ## 计算准确率acc def compute_accuracy(label_var, pred_prob): pred_labels = prob_to_label((pred_prob > 0.5).float(), 1, 0).view(-1) acc = torch.sum(pred_labels == label_var.view(-1)).float() / label_var.size(0) return acc # 5. 模型训练 num_epochs = 10 # 10轮训练 X_train_tensor = torch.tensor(X_train, dtype=torch.float32, device=device) y_train_tensor = torch.tensor(y_train, dtype=torch.float32, device=device).view(-1, 1) for epoch in range(num_epochs): #### Compute outputs #### out = model(X_train_tensor) #### Compute gradients #### cost = cost_fn(out, y_train_tensor) optimizer.zero_grad() cost.backward() #### Update weights #### optimizer.step() #### Logging #### pred_prob = model(X_train_tensor) acc = compute_accuracy(y_train_tensor, pred_prob) print('Epoch: %03d' % (epoch + 1), end="") print(' | Train ACC: %.3f' % acc, end="") print(' | Cost: %.3f' % cost_fn(pred_prob, y_train_tensor)) print('\nModel parameters:') print(' Weights: %s' % model.linear.weight) print(' Bias: %s' % model.linear.bias) # 6. 模型评估 X_test_tensor = torch.tensor(X_test, dtype=torch.float32, device=device) y_test_tensor = torch.tensor(y_test, dtype=torch.float32, device=device) pred_prob = model(X_test_tensor) test_acc = compute_accuracy(y_test_tensor, pred_prob) print('Test set accuracy: %.2f%%' % (test_acc*100)) -
补充1:训练和测试数据的分布
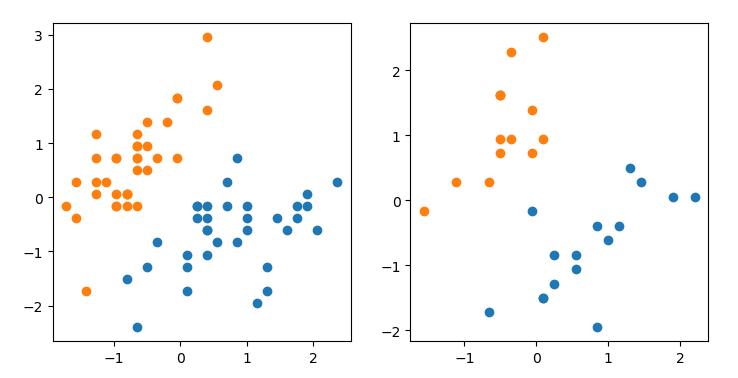
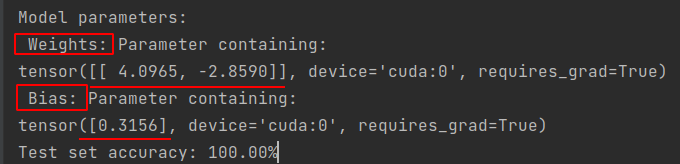
-
补充2:得到的模型参数
9. 疑问厘清
- 逻辑回归假设的是结果服从伯努利分布,而不是每个特征服从伯努利分布
- 逻辑回归对特征的分布类型没有要求,模型学习的是输入特征与目标变量之间的关系,不对特征的具体分布做假设,可以是正太、泊松、均匀分布等等
- 逻辑回归假设的是样本之间独立同分布,而不是特征之间独立同分布
- 特征之间可能是高度相关的,当然这可能会导致模型性能下降或不稳定
- 假设所有样本都是从相同概率分布中抽取,意味着训练集和测试集都来自相同分布,这也是模型能够泛化的原因。所以独立同分布指的是样本的独立同分布
- 高度相关的特征对LR模型有影响,怎么处理:
- 移除一个特征或合并特征:两个特征高度相关,它们可能为模型提供相似信息。合并特征指的是取平均/加权平均/最大最小值等组合
- 使用正则化:正则化可以惩罚高度相关的特征的权重,有助于降低多重共线性对模型的影响
- PCA降维:将原始特征转换为一系列线性不相关的主成分,从而消除多重共线性的影响
- 应用特征选择算法:如之前文章介绍,可以使用递归特征消除法等帮助识别并移除无关或冗余特征,包括与其他特征高度相关的特征
创作不易,如有帮助,请 点赞 收藏 支持
[参考文章]
[1]. 为什么要引入逻辑回归
[2]. LR模型简介
[3]. 公式推导主要参考
[4]. 损失函数的理解
[5]. 损失函数的直观理解
[6]. LR公式画图
[7]. 伯努利分布假设和损失函数推导
[8]. LR应用实例
[9]. 箱线图
[10]. 鸢尾花LR分类实例
[11]. 鸢尾花LR模型分类实践
created by shuaixio, 2024.05.28