2024/6/6 小雨，没停。明天就要高考啦，回想五年前我也带着紧张与期待走过这些天，祝高考学子一切顺利。Anyway，早上一到实验室我就去看望我的栀子花，带着满怀的期待去看它长大了多少，是的，花苞还在叶子上，只不过是睡着的状态！OMG，一瞬的痛苦、难过、自责充斥着我的心。遂搜索原因、怎么正确养护，一直看到现在，同时也购入了相应的肥料。养花真的不简单呐！我是很喜欢花的，这似乎让我与自然更接近。那开始做题吧！

1、题目描述

2、逻辑分析

这是一个很明显的路径规划问题，两点之间有多少种路线。我想不出来，看下题解。看了视频演示就理解了怎么做。简而言之，还是需要回归到规律上，这个动态规划符合那种规律，下图即可很好的解释此规律。

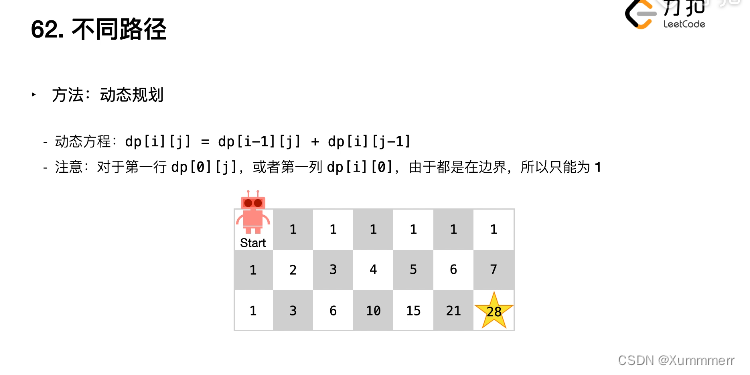
根据以上规律，我们有了相应的计算公式，即可使用代码解释出来。

3、代码演示

public int uniquePaths(int m, int n) {
         // 创建一个二维数组dp，用于存储到达每个位置的不同路径数 
        int [][] dp = new int[m][n];
        // 初始化第一列，因为机器人只能向下移动，所以到达第一列每个位置都只有1条路径
        for(int i = 0 ; i < m; i++){
            dp[i][0] = 1;
        }
        // 初始化第一行，因为机器人只能向右移动，所以到达第一行每个位置都只有1条路径
        for(int j = 0; j < n; j++){
            dp[0][j] = 1;
        }
        // 填充dp数组的其余部分  
        // 使用动态规划的方法，dp[i][j]的值等于其上方位置dp[i-1][j]和左方位置dp[i][j-1]的路径数之和
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }    
        }
        // 返回到达右下角（m-1,n-1）的不同路径数
        return dp[m -1][n -1];
    }

注释解释的很清晰，在这里就画蛇添足

4、复杂度

时间复杂度：O(m * n)。其中 m 和 n 分别是网格的行数和列数。这是因为算法中有两个嵌套的循环，外层循环遍历所有的行（从 1 到 m-1），内层循环遍历所有的列（从 1 到 n-1）。在每次内层循环中，都会执行一次加法操作来更新 dp[i][j] 的值。
空间复杂度：O(m * n)。因为需要一个 m x n 的二维数组 dp 来存储到达每个位置的不同路径数。这个数组的大小与网格的大小直接相关。
还可以使用滚动数组代替代码中的二维数组，使空间复杂度降低为 O(n)，以及数学公式，在这里就不赘述。
那这题就先到这里，再见！