相关博客
【自然语言处理】【Scaling Law】Observational Scaling Laws:跨不同模型构建Scaling Law
【自然语言处理】【Scaling Law】语言模型物理学 第3.3部分:知识容量Scaling Laws
【自然语言处理】Transformer中的一种线性特征
【自然语言处理】【大模型】DeepSeek-V2论文解析
【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM
【自然语言处理】BitNet b1.58:1bit LLM时代
【自然语言处理】【长文本处理】RMT:能处理长度超过一百万token的Transformer
【自然语言处理】【大模型】MPT模型结构源码解析(单机版)
【自然语言处理】【大模型】ChatGLM-6B模型结构代码解析(单机版)
【自然语言处理】【大模型】BLOOM模型结构源码解析(单机版)
论文名称:Observational Scaling Laws and the Predictability of Language Model Performance
论文地址:https://arxiv.org/pdf/2405.10938
一、简介
- Scaling Law能够建立模型规模和效果的联系,但是需要跨不同尺寸来训练模型;
- 本文提出的observational scaling law跳过模型训练的过程,而是从80个公开模型上建立scaling law;
- 从多个模型族中构建scaling law非常有挑战,因为训练的计算代码和能力都在变化。然而,本文展示了这些变化普通的scaling law一致,语言模型的效果是低维能力空间的函数,而模型族的变化仅在将训练计算量转换为能力的效果上不同。
- 使用observational scaling law能够发现复杂缩放线性的可预测性:(1) 一些涌现能力遵循平滑的sigmoidal行为并可以使用小模型预测;(2) agent能力也可以从简单的非agent基准进行预测;(3) 随着语言模型能力的改善,像Chain-of-Thought和Self-Consistency这种post-training技术的影响会怎样变化。
二、Observational Scaling Laws
1. 推广Scaling Laws的计算
在计算scaling laws时,通过会假设模型的计算度量
C
m
C_m
Cm(例如训练的FLOPs)和误差
E
m
E_m
Em(例如困惑度)之间存在幂律关系。具体来说,对于一个属于模型族
f
f
f的模型
m
m
m,会假设
log
(
E
m
)
≈
β
f
log
(
C
m
)
+
α
f
(1)
\log(E_m)\approx\beta_f\log(C_m)+\alpha_f \tag{1}\\
log(Em)≈βflog(Cm)+αf(1)
若这条曲线拟合足够精准的话,那么就能推断出更大计算规模
C
′
>
C
C'>C
C′>C下的模型效果。但是,拟合这样的scaling law并不容易,因为每个模型族
f
f
f和下游基准都有自己的系数
β
f
\beta_f
βf和
α
f
\alpha_f
αf。
一些研究推广函数形式来分析LM在下游任务上的缩放规律。具体来说,令
E
m
E_m
Em表示归一化至区间[0,1]的下游任务误差,其观测到
log
(
C
m
)
\log(C_m)
log(Cm)和
E
m
E_m
Em具有sigmoidal关系,因此使用logistic函数替换等式(1)的对数:
σ
−
1
(
E
m
)
≈
β
f
log
(
C
m
)
+
α
f
(2)
\sigma^{-1}(E_m)\approx\beta_f\log(C_m)+\alpha_f \tag{2}\\
σ−1(Em)≈βflog(Cm)+αf(2)
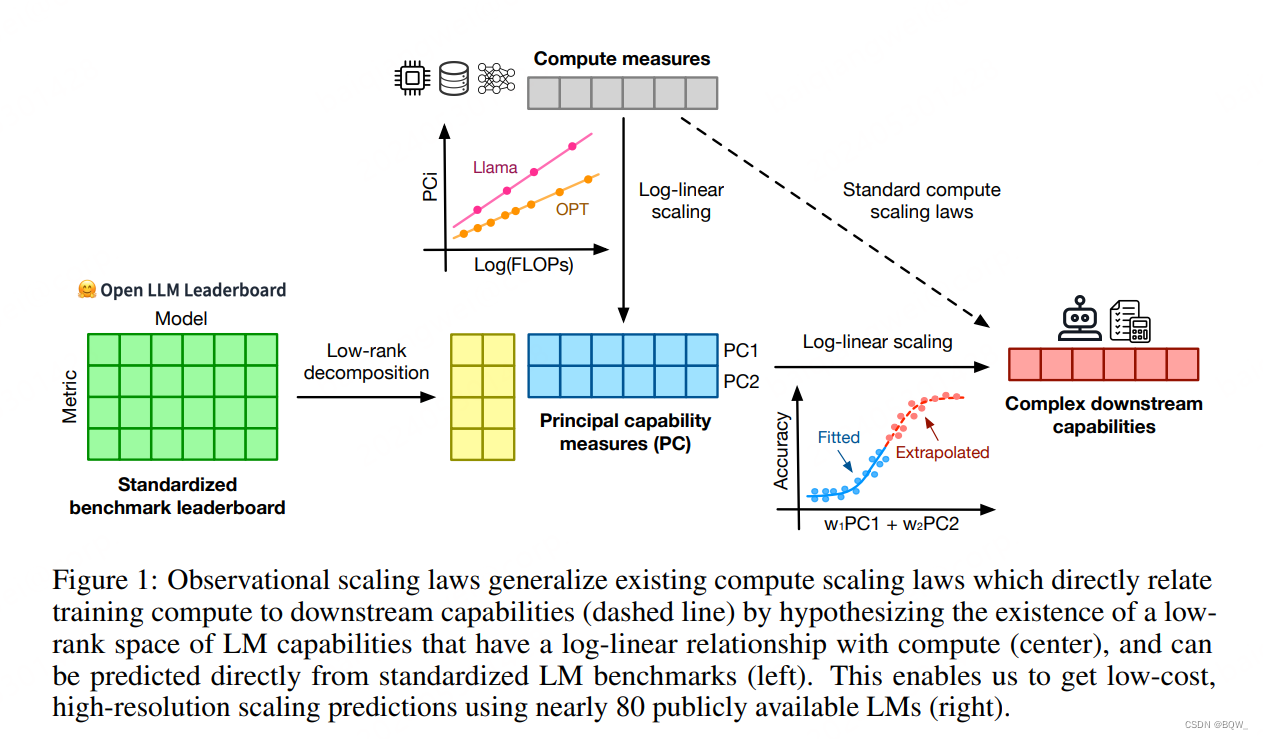
在本文中,假设存在一种LM的低维能力度量,能够将计算量和更复杂的LM能力连接起来,并且从可观测地标准LM基准中抽取出来,如上图1所示。具体来说,给定
T
T
T个简单的基准和模型
m
m
m在基准
i
∈
[
T
]
i\in[T]
i∈[T]上的误差
B
i
,
m
B_{i,m}
Bi,m,假设存在某些能力向量
S
m
∈
R
K
S_m\in\mathbb{R}^K
Sm∈RK满足,
σ
−
1
(
E
m
)
≈
β
⊤
S
m
+
α
S
m
≈
θ
f
log
(
C
m
)
+
v
f
B
i
,
m
≈
γ
i
⊤
S
m
\begin{align} \sigma^{-1}(E_m)&\approx\beta^\top S_m+\alpha \tag{3} \\ S_m&\approx\theta_f\log(C_m)+v_f\tag{4} \\ B_{i,m}&\approx\gamma_i^\top S_m \tag{5} \\ \end{align} \\
σ−1(Em)SmBi,m≈β⊤Sm+α≈θflog(Cm)+vf≈γi⊤Sm(3)(4)(5)
其中
θ
f
,
v
f
,
β
∈
R
K
,
α
∈
R
\theta_f,v_f,\beta\in\mathbb{R}^K,\alpha\in\mathbb{R}
θf,vf,β∈RK,α∈R,并且正交向量
γ
i
∈
R
K
\gamma_i\in\mathbb{R}^K
γi∈RK。
等式(3)和(4)是等式(2)的推广,因为合并这两个等式就能够恢复单个模型族的原始缩放关系。然而,当有多个模型族时, S m S_m Sm作为一个共享的模型能力低维空间,所有下游度量(E和B)都是从该空间派生出来的,模型族将计算转换为能力的效率上有所不同(等式(4))。等式(4)的一种解释, θ f \theta_f θf表示模型族 f f f的计算效率, S m S_m Sm是模型族的log-FLOPs所表示的模型 m m m的能力。
最终,等式(5)确保这些能力不是用来估计每个模型族的隐变量,而是完整可观测属性(B)的函数。因为 γ ∈ R K × T \gamma\in\mathbb{R}^{K\times T} γ∈RK×T是正交的,可以线性估计 S ^ m : = γ B m \hat{S}_m:=\gamma B_m S^m:=γBm。
2. 确定低维能力空间(等式(5))
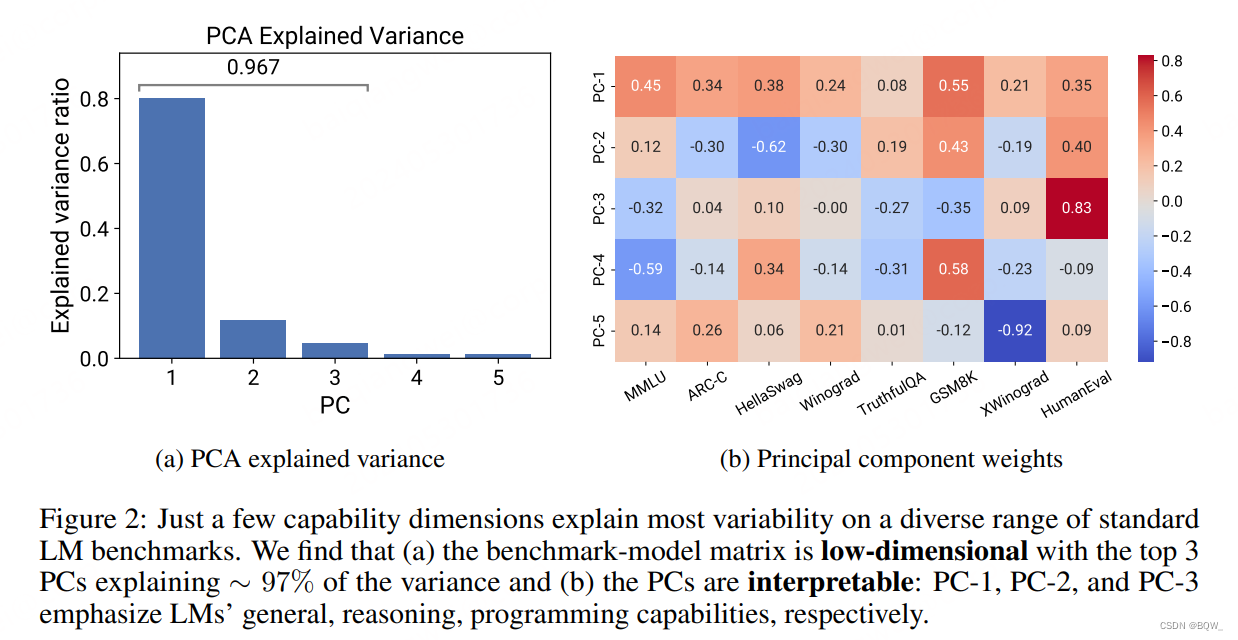
这里验证存在低维能力度量 S S S,其与标准LM基准B线性相关。采用的方式是证明B中仅有少量主成分捕获了其变化的绝大部分。这里证明了"基准-模型"矩阵 B B B是低秩的,并且等式(5)是合理假设。这种方式极大依赖于模型和基准的选择,下面描述选择的过程。
模型。收集了广泛了开源模型,包括21个模型族共计77个模型。这些模型包括使用标准方式训练出来的LLaMA和Qwen,也包含在合成数据上训练的Phi,以及在代码数据上训练的CodeLlama和StarCoder等。为了避免指令微调带来的复杂性,这里仅对base模型进行分析。
基准。收集了用于评估LM能力的各种基准,包括MMLU、ARC-C、HellaSwag、Winograndle、GSM8K、HumanEval、TruthfulQA、XWinograd等。
PCA分析。在获得了LM基准度量,进一步解决缺失值问题,这主要是由评估失败导致的。随后,使用PCA来抽取评估度量的主成分,作为衡量 S S S的"principal capability"(PC)。
PC度量是低维的。可以观察到抽取的PC度量是低秩的,top 3的PCs能够解释97%的变化,这个结果表明基准B是低维的(上图2a)。此外,发现仅第一PC就能解释LM能力变化的80%。仔细观察这些PCs,可以发现这些能力度量代表了可解释方向,LM的能力可以自然地作为规模的函数。具体来说,PC-1表示通用能力;PC-2对于"推理能力",着重在数学和代码基准上;PC-3则主要反映了编程能力。这些发现表明,许多简单的LLM能力都可以表示为少数"principal capabilities"的线性组合。
3. Principal Capability度量作为规模度量的替代(等式(4))
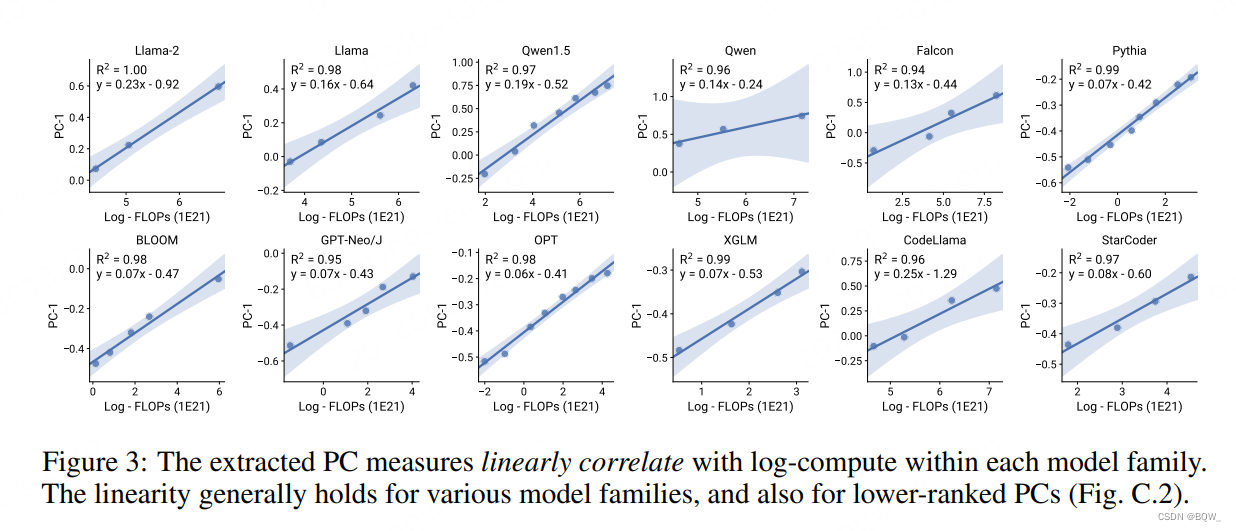
设定。对于每个模型,收集关于训练FLOPs所有可用信息,分析论文和其他公共信息来确定模型的尺寸N和预训练数据尺寸D。对于能够明确这些信息的模型,使用简单估计 C ≈ 6 N D C\approx 6ND C≈6ND来获得模型训练的FLOPs。
PC度量与对数计算量度量线性相关。上图3展示了PC-1度量与模型训练FLOPs的关系。可以发现,LM的PC-1度量都与对数训练FLOPs线性相关。这种线性相关性在各种模型上都成立,包括多语言模型BLOOM以及代码模型StarCoder。这种现象在PC-2和PC-3这种较低的PC上也成立。总的来说,这些结果支撑了等式(4)和等式(5)的有效性,即假设模型共享相同的能力空间,并且每个模型的计算量和这些principal capabilities是对数线性关系。
4. 拟合Observational Scaling Laws
算法A.1:拟合observational scaling laws
参数:模型数量 M M M,基准数量 T T T,主成分数量 K K K,模型族 f f f
输入:base语言模型的误差度量 B ∈ R T × M B\in\mathbb{R}^{T\times M} B∈RT×M,目标下游误差度量 E ∈ R M E\in\mathbb{R}^M E∈RM,语言模型计算量规模 C ∈ R M C\in\mathbb{R}^M C∈RM
结果:函数形式的拟合后scaling law F F F
/* 抽取主成分 */
B ← PCAImpute ( B ) B\leftarrow\text{PCAImpute}(B) B←PCAImpute(B) // 填充缺失值
E ← Normalize ( E ) E\leftarrow\text{Normalize}(E) E←Normalize(E) // 将度量归一化至区间[0,1]
γ , S ← PCA ( B , K ) \gamma,S\leftarrow\text{PCA}(B,K) γ,S←PCA(B,K) // 拟合PCA变换 γ ∈ R K × T \gamma\in\mathbb{R}^{K\times T} γ∈RK×T并抽取主成分 S = γ B S=\gamma B S=γB
/* 拟合非线性回归 */
β ∗ , α ∗ , h ∗ ← Fit ( E = h σ ( β ⊤ S + α ) ) \beta^*,\alpha^*,h^*\leftarrow \text{Fit}(E=h\sigma(\beta^\top S+\alpha)) β∗,α∗,h∗←Fit(E=hσ(β⊤S+α)) // 获得最优系数
P ← β ∗ ⊤ S + α ∗ P\leftarrow \beta^{*\top}S+\alpha^* P←β∗⊤S+α∗ // 获得聚合能力度量 P ∈ R M P\in\mathbb{R}^M P∈RM
/* 投影到参考模型族的能力等效规模上 */
w ∗ , b ∗ ← Fit ( P f = w log ( C f ) + b ) w^*,b^*\leftarrow\text{Fit}(P_f=w\log(C_f)+b) w∗,b∗←Fit(Pf=wlog(Cf)+b)
log ( C ˉ f ) ← ( P − b ∗ ) / w ∗ \log(\bar{C}_f)\leftarrow(P-b^*)/w^* log(Cˉf)←(P−b∗)/w∗ // 为所有模型计算 f − equivalent FLOPs f-\text{equivalent FLOPs} f−equivalent FLOPs
/* 返回基于能力等效规模变换的scaling law */
return F : B → h ∗ σ ( β ∗ ⊤ γ B + α ∗ ) F:B\rightarrow h^*\sigma(\beta^{*\top}\gamma B+\alpha^*) F:B→h∗σ(β∗⊤γB+α∗)或者 C ˉ f → h ∗ σ ( w ∗ log ( C ˉ f ) + b ∗ ) \bar{C}_f\rightarrow h^*\sigma(w^*\log(\bar{C}_f)+b^*) Cˉf→h∗σ(w∗log(Cˉf)+b∗)
使用简单的主成分分析就能获得能力度量 S S S,近似满足等式(4)和等式(5)。现在来估计等式(3)中的缩放关系。完整算法见算法A.1。
用PC度量拟合回归。给定归一化至区间[0,1]的下游误差度量
E
E
E,简单推广等式(3)有
E
m
≈
h
σ
(
β
⊤
S
m
+
α
)
(6)
E_m\approx h\sigma(\beta^\top S_m+\alpha) \tag{6}\\
Em≈hσ(β⊤Sm+α)(6)
其中
β
∈
R
K
\beta\in\mathbb{R}^K
β∈RK和
α
∈
R
\alpha\in\mathbb{R}
α∈R是回归的权重和偏差,
h
∈
[
0
,
1
]
h\in[0,1]
h∈[0,1]负责调整缩放的因子。使用普通的最小二乘法并限制
h
∈
[
0.8
,
1.0
]
h\in[0.8,1.0]
h∈[0.8,1.0]。
定义可解释性的计算量度量。回想一下,本文中的scaling law的核心组件就是拟合线性变换
P
m
:
=
β
∗
S
m
+
α
∗
P_m:=\beta^* S_m+\alpha^*
Pm:=β∗Sm+α∗,其能够将抽取的主成分(PCs)映射到下游度量标量值上。虽然这对于预测来说是完全可以接受的,但是若能够将其表示为FLOPs而不是任意标量能力度量的话,进一步的缩放分析将更加能够解释。等式(3)和等式(4)所表达的observational scaling laws是单个模型族计算量scaling law的推广。具体来说,若等式(4)完全成立,对于在模型族
f
f
f中的模型
m
m
m有
P
m
:
=
β
∗
⊤
S
m
+
α
∗
=
w
f
log
(
C
m
)
+
b
f
(7)
P_m:=\beta^{*\top}S_m+\alpha^*=w_f\log(C_m)+b_f\tag{7} \\
Pm:=β∗⊤Sm+α∗=wflog(Cm)+bf(7)
其中
w
f
=
β
∗
⊤
θ
f
w_f=\beta^{*\top}\theta_f
wf=β∗⊤θf且
b
f
=
β
∗
⊤
v
f
+
α
∗
b_f=\beta^{*\top}v_f+\alpha^*
bf=β∗⊤vf+α∗。这也意味着标量能力
P
m
P_m
Pm和特定模型族中模型计算量
log
(
C
)
\log(C)
log(C)存在线性关系。由于
θ
f
\theta_f
θf和
v
f
v_f
vf是未知先验,可以通过从
log
(
C
)
\log(C)
log(C)到
P
P
P的线性回归来拟合系数
w
f
w_f
wf和
b
f
b_f
bf。
在多模态族的情况下,计算效率的变化意味着跨模型族的FLOPs和能力不再试对数线性关系。然而,可以将所有的模型都映射到一个共享的、基于FLOPs的能力度量上,这种度量称为
f
-equivalent
FLOPs
f\textbf{-equivalent FLOPs}
f-equivalent FLOPs。该方法的核心是通过以下假设来表示每个模型的能力:“模型族
f
f
f中的模型需要多少
log
-FLOPs
(
log
(
C
ˉ
m
,
f
)
)
\log\text{-FLOPs}(\log(\bar{C}_{m,f}))
log-FLOPs(log(Cˉm,f))才能匹配模型m”。这里称
log
(
C
ˉ
m
,
f
)
\log(\bar{C}_{m,f})
log(Cˉm,f)是模型
m
m
m的
f-equivalent FLOP
\text{f-equivalent FLOP}
f-equivalent FLOP,因为其代表了模型
m
m
m相对于模型族
f
f
f中的模型性能。这个度量的计算为
log
(
C
ˉ
m
,
f
)
:
=
1
w
f
∗
(
β
∗
⊤
S
m
+
α
∗
−
β
∗
)
(8)
\log(\bar{C}_{m,f}):=\frac{1}{w_f^*}(\beta^{*\top}S_m+\alpha^*-\beta^*) \tag{8} \\
log(Cˉm,f):=wf∗1(β∗⊤Sm+α∗−β∗)(8)
通过求解等式(7)中的
log
(
C
m
)
\log(C_m)
log(Cm)即可得到。
三、验证Observational Scaling Laws
通过展示observational scaling laws能够准确预测LM在复杂且难以预测现象(例如涌现现象和agent能力)上的能力来展示其有用性。
scaling law拟合细节。抽取的主成分数量 K = 3 K=3 K=3,因为其已经能力覆盖约97%的变化并且在大多数实验中效果最好。对于能力等效规模变换,使用Llama-2作为参考模型族。为了有更好的解释性和可视化,使用准确率作为度量进行scaling law拟合并绘制。
1. 涌现能力的可预测性
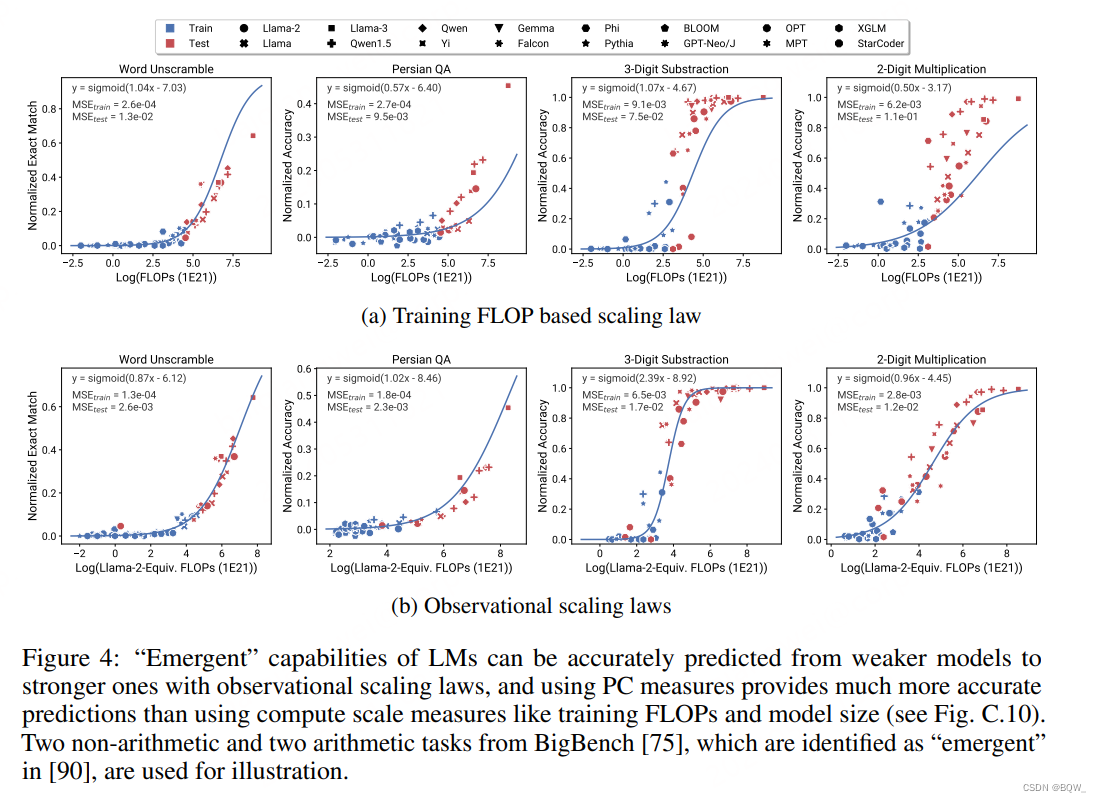
近期的一些研究认为许多LM的能力是"涌现"的,并不能轻易通过小模型来预测。能力的不连续变化是的开发大规模的算法和基准变得困难。此外,一直存在争论是否真的不连续还是度量的分辨率不高。
高分辨率的observational scaling laws能够使得我们对涌现能力观察到更光滑的sigmoidal曲线。此外,仅通过效果略比随机效果好的模型就可以预测从接近随机到很好效果的转换点。
从BigBench中挑选了Wei et al认为的涌现任务进行测试,包括2个算术任务和2个非算术任务。结果如上图4所示,可以发现使用PC度量能够准确预测这些能力,甚至仅使用表现较差的模型。相反,使用训练的FLOPs会导致外推的效果差并拟合至训练集。这可能是因为不同模型族的训练FLOPs的不可比较性。
2. Agent能力的可预测性
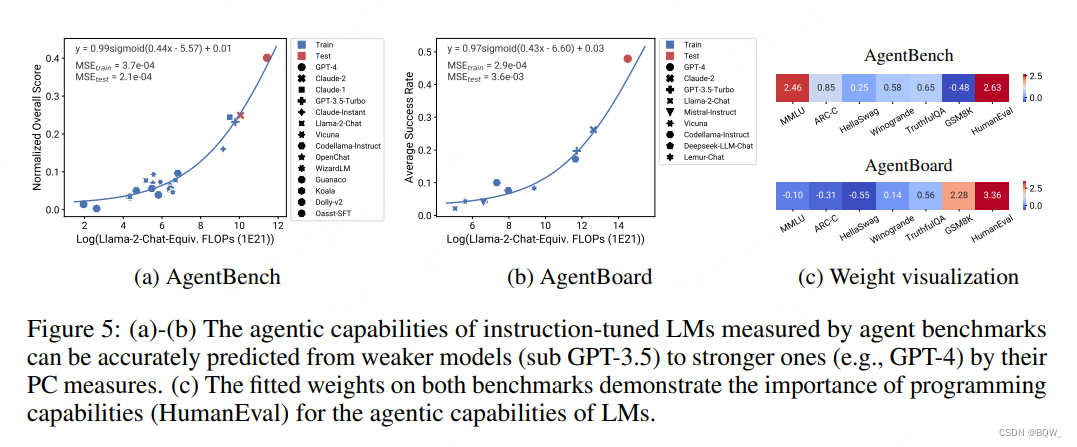
人们对于使用LLM构建Agent非常感兴趣,例如AutoGPT、Devin和SWE-agent。虽然这些agent在有挑战的真实世界任务上远远落后于人类水平,但是未来更大的模型将会显著增强这些agent的能力。然而,对于在语言和代码任务上训练的模型是否能够很好的迁移至需要采取许多轮的agent任务上,仍然存在很大的不确定性。本节,利用observational scaling laws来分析LM agent能力的缩放性质。
测试两个标准的agent评估基准AgentBench和AgentBoard,这两个基准都是评估语言模型通过代理能力的基准。结果如上图5所示,可以发现在两个基准上都可以使用非常弱的模型来准确预测。这也表明语言模型的agent能力与其基本能力有很好的相关性,随着LM模型结果继续增大则agent能力会继续增强。
如图5c所示,其可视化了两个基准上的基础评估度量,这些度量是由PC度量拟合的回归权重得到的。可以发现,两个基准在编程能力上都分配了很多的权重,这表明编程能力对于Agent的重要性。此外,AgentBench中对通用知识(MMLU)分配了更多权重,而AgentBoard则是更需要推理能力(GSM8K),这也表明这些能力对Agent同样重要。
3. Post-Training技术影响的预测
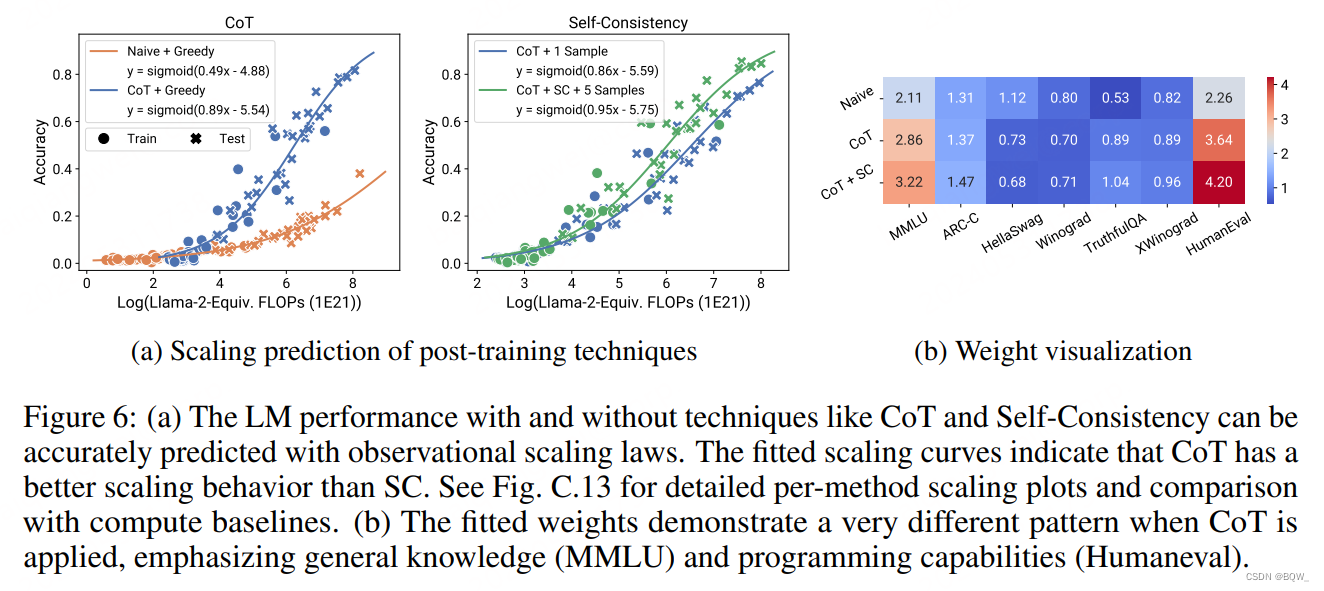
当研究人员提出新的prompting或者post-training技术来改善预训练模型时,我们是否能够确定这些收益是否能够跨模型和规模而持续存在呢?Scaling分析能够为post-training技术的设计提供更加定量的方法,但是由于单个模型族中模型数量太少,导致缺乏系统的scaling分析。除了这些挑战外,一些研究认为像CoT这样的干预技术是涌现的,无法从更小的模型上预测。使用observational scaling laws,能够相对准确的预测Chain-of-Thought和Self-Consistency等技术的影响和模型规模的关系。
量化post-training技术缩放性质的方法很直接:在目标基准(例如GSM8K)上使用base模型的效果来拟合observational scaling law,然后使用post-training干预技术(GSM8K w/ CoT)后的效果在拟合observational scaling law。每次拟合都会产生一个sigmoidal缩放曲线,其作为 log ( C ˉ f ) \log(\bar{C}_f) log(Cˉf)的函数,两个曲线的相对差距作为 log ( C ˉ f ) \log(\bar{C}_f) log(Cˉf)的函数来表示干预技术的缩放效率。
在GSM8K上测试了post-training技术CoT和SC,结果如上图6所示。可以发现,使用post-training技术(CoT,CoT+SC)和不使用post-training技术都能够通过较小的模型来准确预测较大的模型。相比之下,基于模型尺寸或者训练FLOPs这种计算规模的度量进行预测并不是特别可靠。显然,两种技术的缩放趋势并不相同,CoT相比于Self-Consistency w/CoT具有更明显的缩放趋势。
observational scaling law相比于基于单个模型族的scaling law的另一个优势,能够可视化对于post-training技术更重要的能力。上图6b可视化了拟合的回归权重 β \beta β,其通过 β ⊤ γ \beta^\top\gamma β⊤γ映射到基本能力基准 B B B的空间上。可以清洗的看到,从Naive到CoT,MMLU和HumanEval的权重明显更高,这意味着通过增强通用知识(MMLU)和代码(HumanEval)的方式缩放模型能够使得baseline和CoT的差距更大,而改善常识(Winogrande)并不能带来显著的改善。
四、挑选低成本模型子集进行Scaling分析(略)
五、Observational Scaling其他应用(讨论)
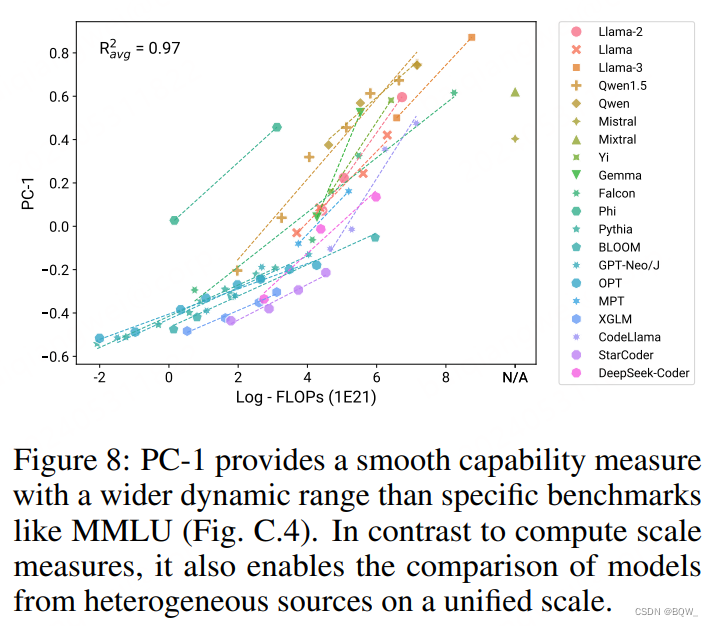
PC-1作为高动态范围的平滑能力度量。
许多现有基准的动态范围有限:对于大模型很快饱和或者对于小模型完全随机。相反,PC-1是能够跨不同量级来比较LM的平滑能力度量。这允许我们在单一且统一尺度上来比较不同来源且能力极度不同的模型,如上图8所示。本文认为PC1的高动态范围使其更适合作为预训练的优化目标。
使用PC-1衡量训练数据效率。
由于PC-1能够作为统一的能力度量,那么其能够作为跨不同模型族比较计算效率的好方法。在图8中绘制了PC-1与log-FLOPs的关系,发现大多数模型在"训练计算-能力"曲线上都有清晰的模式。Phi模型在计算效率时是显著的异常点,这可能是因为没有考虑其用于生成训练数据所消耗的额外推理FLOPs。
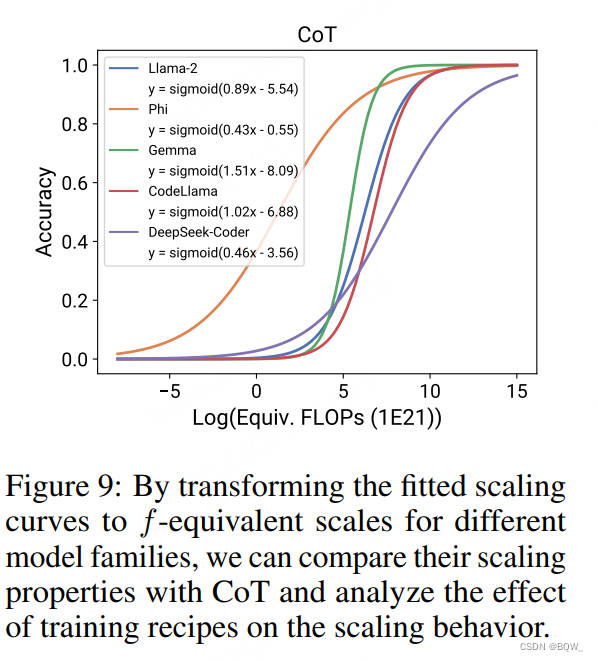
Post-training技术与模型族的交互。
可以进一步分析post-training技术和模型族之间的交互,确定出哪些模型族能够从这些技术中受益最大,以及受益的起始点。上图9是不同模型族之间CoT的影响,可以发现模型都可以从CoT中受益,但是Phi再次成为异常值:其从CoT受益要比其他模型更早,但是速度慢很多。类似地,在代码数据上训练的DeepSeek-Coder也展现出了较早的过渡和较慢的增速。Phi/DeepSeek-Coder相较于其他模型的独特行为也表明了预训练数据对于模型scaling行为的影响。
益的起始点。上图9是不同模型族之间CoT的影响,可以发现模型都可以从CoT中受益,但是Phi再次成为异常值:其从CoT受益要比其他模型更早,但是速度慢很多。类似地,在代码数据上训练的DeepSeek-Coder也展现出了较早的过渡和较慢的增速。Phi/DeepSeek-Coder相较于其他模型的独特行为也表明了预训练数据对于模型scaling行为的影响。