1.冯诺依曼结构
传统计算机采用冯●诺依曼(Von Neumann)结构,也称普林斯顿结构,是一种将程序指令存储器和数据存储器合并在一起的存储器结构。

特征:
- 冯●诺依曼结构的计算机程序和数据共用一个存储空间,程序指令存储地址和数据存储地址指向同一个存储器的不同物理位置。
- 采用单一的地址及数据总线,程序指令和数据的宽度相同。
- 处理器执行指令时,先从储存器中取出指令解码,再取操作数执行运算,即使单条指令也要耗费儿个甚至几十个周期,在高速运算时,在传输通道上会出现瓶颈效应。
2.哈佛结构
哈佛结构是一种并行体系结构,它的主要特点是将程序和数据存储在不同的存储空间中,即程序存储器和数据存储器是两个相互独立的存储器,每个存储器独立编址、独立访问。
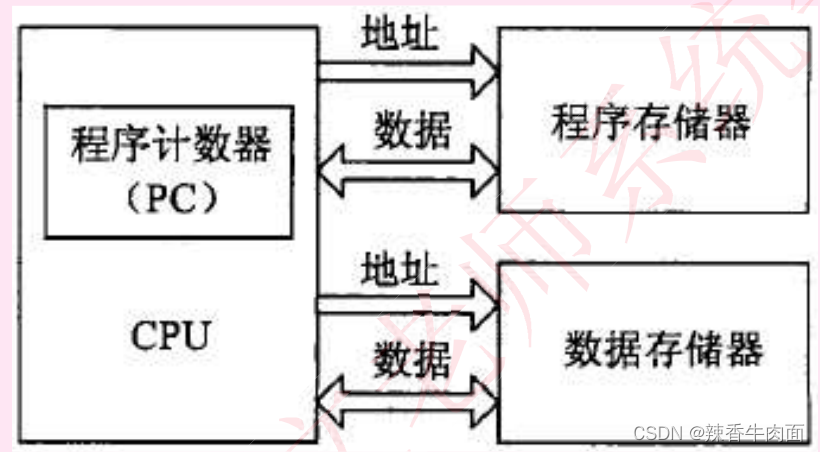
特征:
- 与两个存储器相对应的是系统中的两套独立的地址总线和数据总线。
- 这种分离的程序总线和数据总线可允许在一个机器周期内同时获取指令字(来自程序存储器)和操作数(来自数据存储器),从而提高了执行速度,使数据的吞吐率提高了1倍。
- 但这不意味着可以在一个机器周期内多次访问存储器。