目录

前言

曼彻斯特编码

定义

策略

思路

差分曼彻斯特编码

定义

策略

思路

结束语

---

前言

今天是坚持写博客的第十九天，很高兴自己又坚持了一天，今天想送给自己一句李白《行路难》当中的诗词，希望我自己和大家都可以铭记于心，相互勉励：行路难，行路难，多歧路，今安在？长风破浪会有时，直挂云帆济沧海。

我们今天来讲计算机网络当中的曼彻斯特编码和差分曼彻斯特编码。

---

曼彻斯特编码

定义

曼彻斯特编码是目前应用最为广泛的一种编码方式，用于在数据通信中同步信号和时钟信号，解决同步问题。主要特点是每比特的中间有一次电平跳转，两次电平跳转的间隔可以是T/2或T，利用电平跳转可产生首发双方的同步信号。但是缺点是效率低，占用带宽大。

其中比特“0”的编码是从高电平到低电平；比特“1”的编码是从低电平到高电平。

曼彻斯特编码的规则如下：

1. 每比特的周期T分为前T/2和后T/2两部分。
2. 前T/2传送该比特的反码，后T/2传送该比特的原码。

策略

假设我们现在有一段二进制编码0100110，我们要使用曼彻斯特编码的方式将其表示出来，我们可以遵循以下步骤：遇到“0”时从高处出发，遇到“1”时从低处出发。

因此我们可以很快得出解题思路与图解。

思路

解题思路如下（配合图解看可能理解起来会更加容易）：

1. 首先第一个是“0”，从高处（高电平）出发到低处（低电平）。
2. 第二个是“1”，从低处（低电平）出发到高处（高电平）。
3. 第三个是“0”，从高处（高电平）出发到低处（低电平）。
4. 第四个是“0”，依旧是从高处（高电平）出发到低处（低电平）。
5. 第五个是“1”，从低处（低电平）出发到高处（高电平）。
6. 以此类推，我们可以得到如下的图解：

如果遇到连续两个编码或者多个编码相同，比如“00”，那么在第一个“0”到低处后，我们需要立即回到高处，进行对下一个“0”的编码，“11”也同理，第一个“1”到高处后需要立即到低处进行下一个编码。

---

差分曼彻斯特编码

定义

差分曼彻斯特编码与曼彻斯特编码类似，但它关注的是相邻比特之间的电平变化，而不是每个比特周期内的电平变化。规则如下：

1. 没比特的中间跳变仅用于同步。
2. 根据每比特的开始便捷是否跳转来决定该比特的值。
3. 每比特的开始处如果发生电平跳变，这传输“0”，否则传输“1”。

策略

我们仍然使用编码0100110，我们要使用差分曼彻斯特编码的方式将其表示出来，我们可以遵循以下步骤：如果下一个是“1”那么交界处的“线段”不变，如果下一个是“0”吗，饿交界处的“线段”变化。

因此我们也可以快速得到如下思路和图解。

思路

解题思路如下（配合图解看可能理解起来会更加容易）：

1. 第一个是“0”，不受影响，先从高处（高电平）出发到低处（低电平）。
2. 第二个是“1”，因为此时“即将”到来的是“1”，因此交界处的“线段”不变。
3. 第三个是“0”，此时“即将”到来的是“0”，因此交界处的“线段”变。
4. 第四个是“0”，此时“即将”到来的是“0”，因此交界处的“线段”变。
5. 第五个是“1”，此时“即将”到来的是“1”，因此交界处的“线段”不变。
6. 第六个是“1”，此时“即将”到来的是“1”，因此交界处的“线段”不变。
7. 以此类推，我们可以得出如下图解：

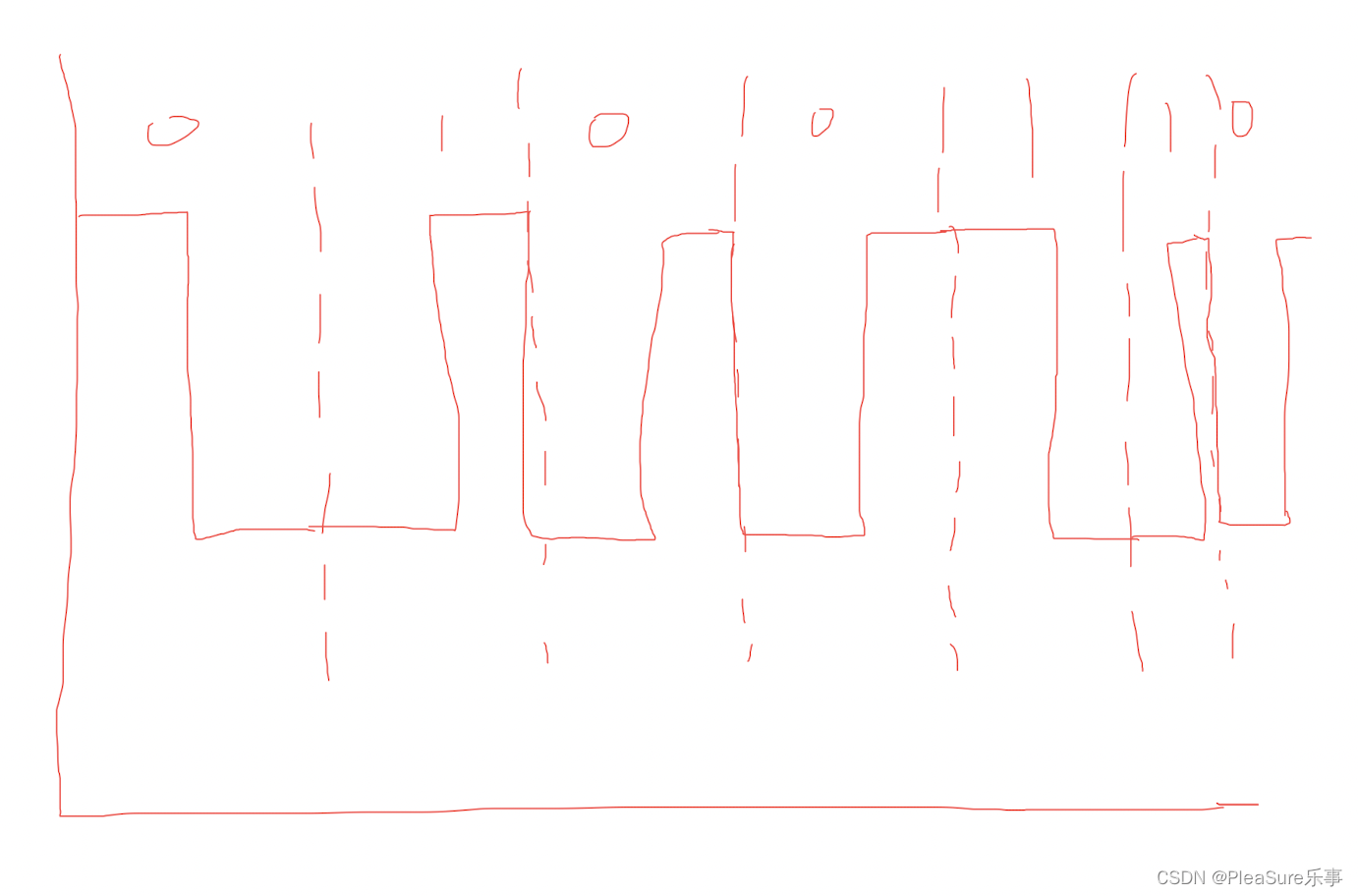
简化下来记忆，其实可以遵循“遇到1延长，遇到0上升/下降”的口诀，这样可以方便记忆，而不至于走错路。

---

结束语

今天对曼彻斯特编码和差分曼彻斯特编码的讲解就到这里，希望对大家有所帮助，如果对您有帮助，希望您可以留下点赞、关注和收藏，这对我很重要，谢谢！