1、fft 快速傅里叶变换
语法
Y = fft(X) 使用快速傅里叶变换 (FFT) 算法计算 X 的离散傅里叶变换 (DFT)。
Y = fft(X,n) 返回 n 点 DFT。
Y = fft(X,n,dim) 返回沿维度 dim 的傅里叶变换。例如,如果 X 是矩阵,则 fft(X,n,2) 返回每行的 n 点傅里叶变换含噪信号
1)原始信号加噪声
代码
Fs = 1000;
T = 1/Fs;
L = 1500;
t = (0:L-1)*T;
%振幅为 0.8 的 DC 偏移量、振幅为 0.7 的 50 Hz 正弦量和振幅为 1 的 120 Hz 正弦量。
%w/2Pi=频率
S = 0.8 + 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
%均值为零、方差为 4 的随机噪声扰乱该信号。
X = S + 2*randn(size(t));
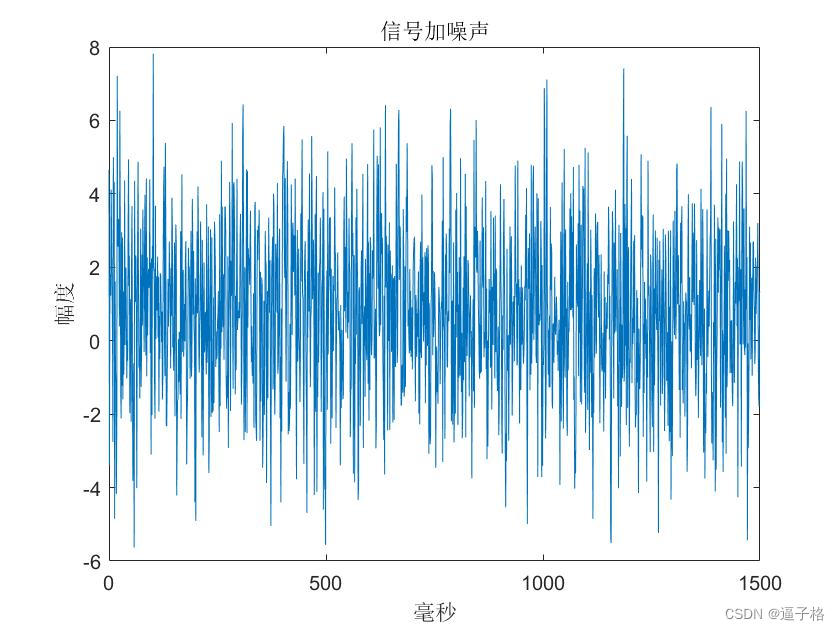
plot(1000*t,X)
title("信号加噪声")
xlabel("毫秒")
ylabel("幅度")视图效果
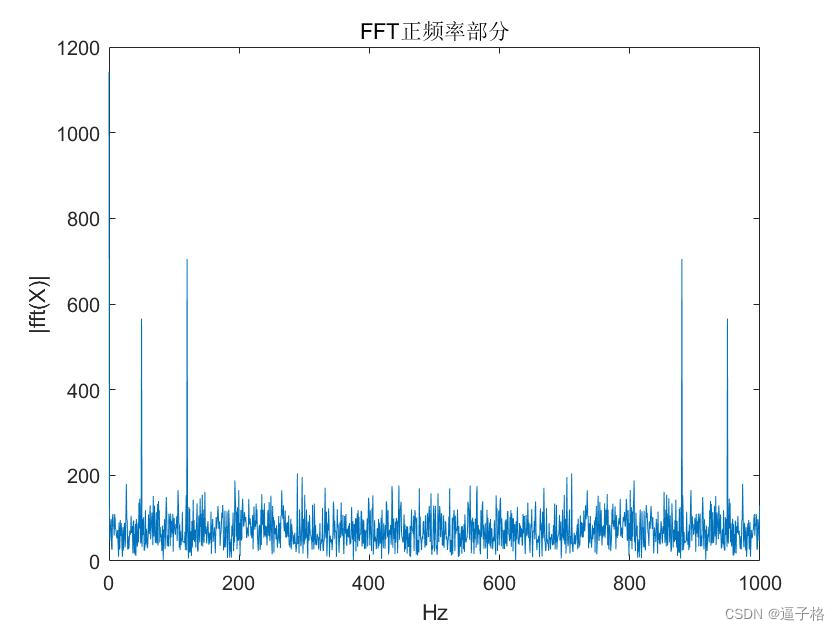
2)傅里叶变换显示正频率部分
代码
Y = fft(X);%傅里叶变换
plot(Fs/L*(0:L-1),abs(Y))%复数求模
title("FFT正频率部分")
xlabel("Hz")
ylabel("|fft(X)|")视图效果
3)傅里叶变换显示全频率部分
代码
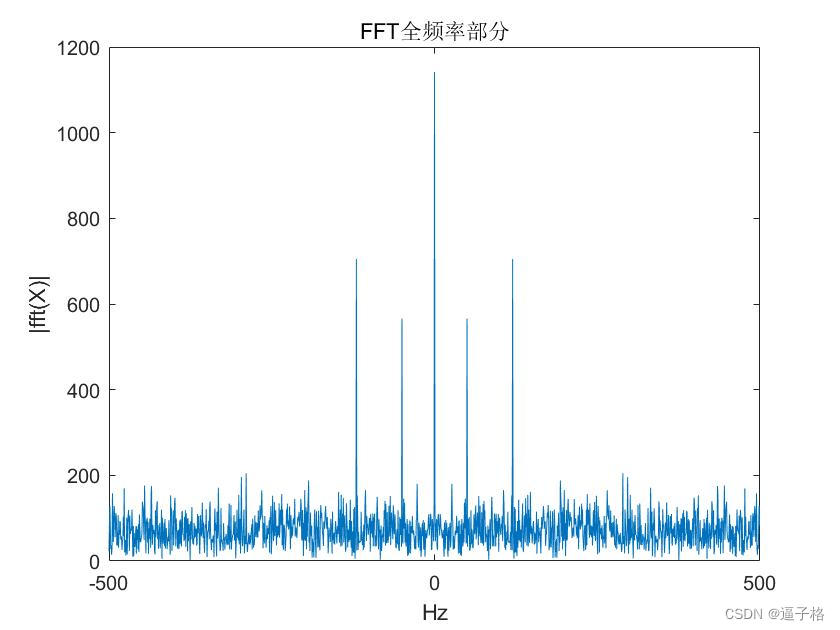
%该图显示五个频率峰值,包括 DC 偏移量在 0 Hz 处的峰值。
%在此示例中,信号预计在 0 Hz、50 Hz 和 120 Hz 处有三个
%频率峰值。此处,绘图的后半部分是前半部分的镜像,
plot(Fs/L*(-L/2:L/2-1),abs(fftshift(Y)))%fftshift 显示正负频率
title("FFT全频率部分")
xlabel("Hz")
ylabel("|fft(X)|")视图效果
4) 精确检索振幅
代码
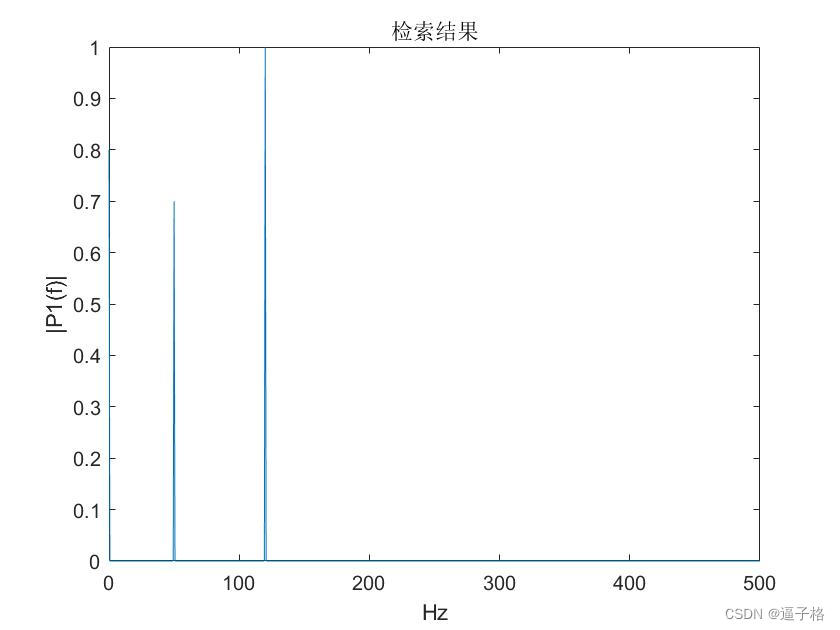
%采用原始的、未破坏信号的傅里叶变换并检索精确振幅在 0.8、0.7 和 1.0 处。
f = Fs/L*(0:(L/2));
Y = fft(S);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
plot(f,P1)
title("检索结果")
xlabel("Hz")
ylabel("|P1(f)|")视图效果
2、 高斯脉冲
1)时域脉冲信号
代码
%高斯脉冲
Fs = 44100;
T = 1/Fs;
t = -0.5:T:0.5;
L = length(t);
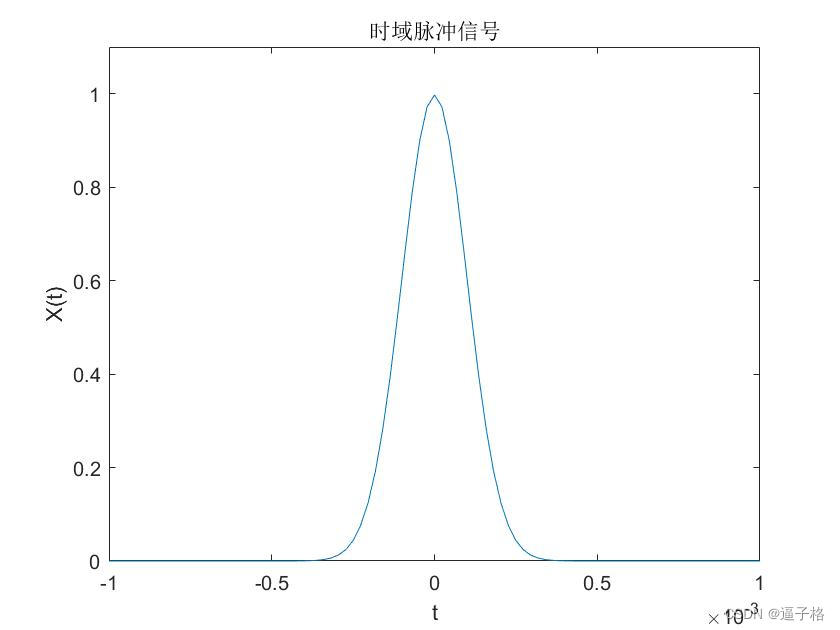
X = 1/(0.4*sqrt(2*pi))*(exp(-t.^2/(2*(0.1*1e-3)^2)));
plot(t,X)
title("时域脉冲信号")
xlabel("t")
ylabel("X(t)")
axis([-1e-3 1e-3 0 1.1])视图效果
2)傅里叶变换
代码
n = 2^nextpow2(L);%2次幂输入长度
Y = fft(X,n);
f = Fs*(0:(n/2))/n;
P = abs(Y/sqrt(n)).^2;
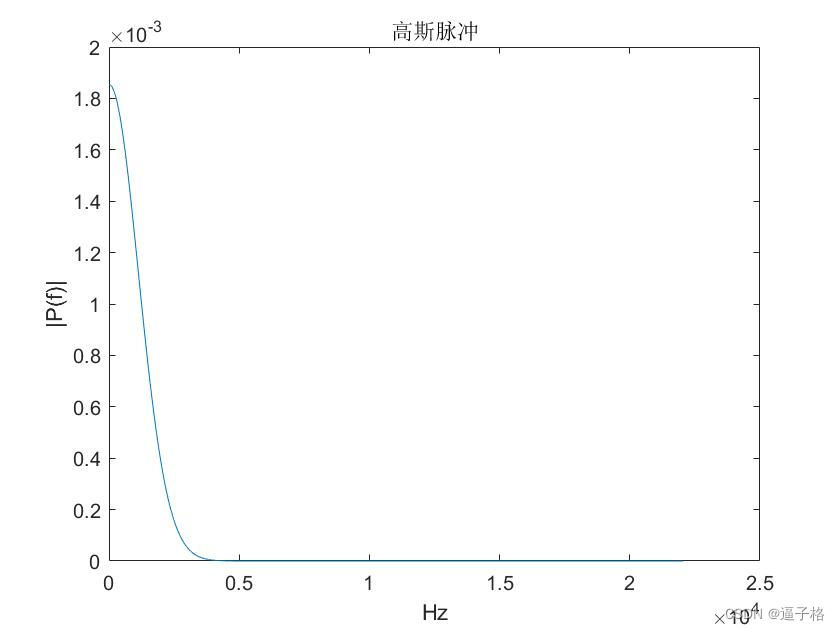
plot(f,P(1:n/2+1))
title("高斯脉冲")
xlabel("Hz")
ylabel("|P(f)|")视图效果
3、余弦波
1)时域效果
代码
%3余弦波
Fs = 1000;
T = 1/Fs;
L = 1000;
t = (0:L-1)*T;
x1 = cos(2*pi*50*t);
x2 = cos(2*pi*150*t);
x3 = cos(2*pi*300*t);
X = [x1; x2; x3];
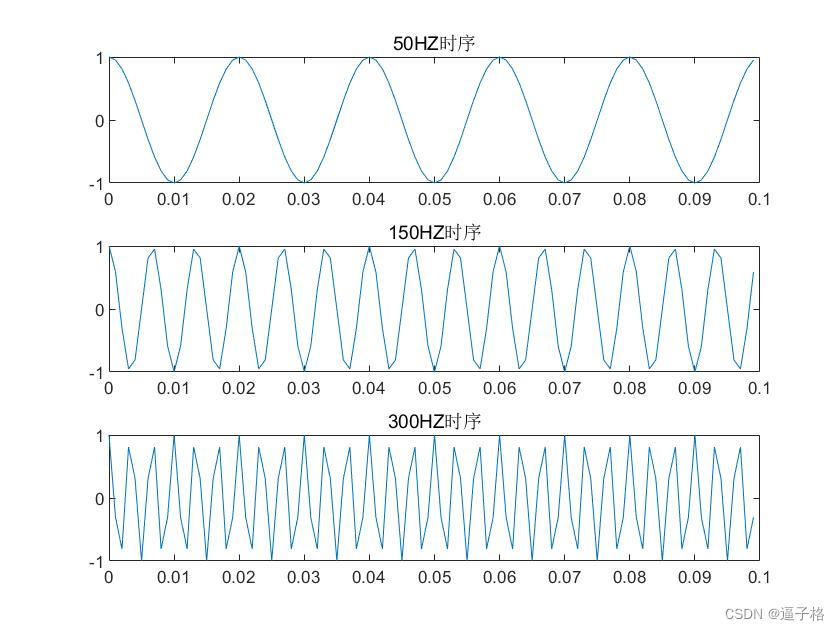
subplot(3,1,1)
plot(t(1:100),X(1,1:100))
title('50HZ时序')
subplot(3,1,2)
plot(t(1:100),X(2,1:100))
title('150HZ时序')
subplot(3,1,3)
plot(t(1:100),X(3,1:100))
title('300HZ时序')视图效果
2)傅里叶变换
代码
dim = 2;%行方向
Y = fft(X,L,dim);
P2 = abs(Y/L);
P1 = P2(:,1:L/2+1);
P1(:,2:end-1) = 2*P1(:,2:end-1);
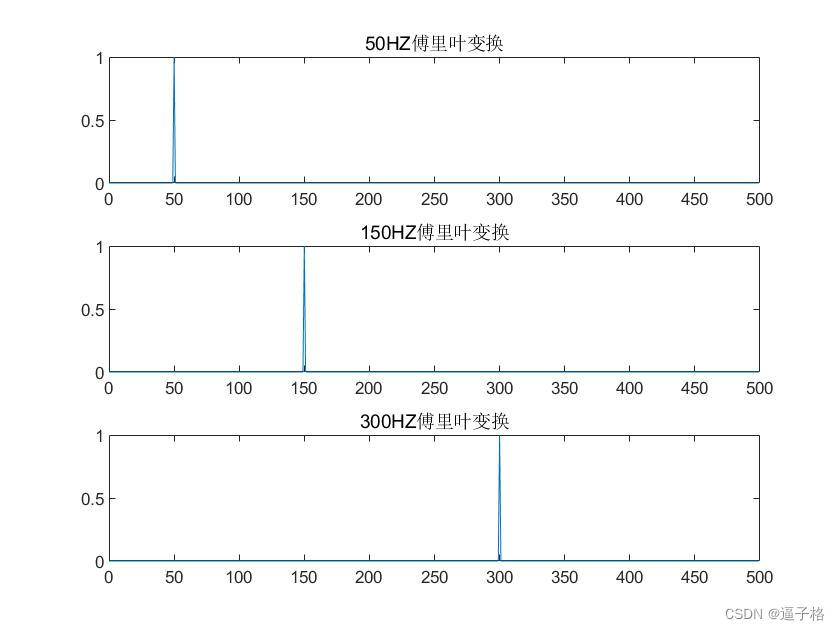
subplot(3,1,1)
plot(0:(Fs/L):(Fs/2-Fs/L),P1(1,1:L/2))
title('50HZ傅里叶变换')
subplot(3,1,2)
plot(0:(Fs/L):(Fs/2-Fs/L),P1(2,1:L/2))
title('150HZ傅里叶变换')
subplot(3,1,3)
plot(0:(Fs/L):(Fs/2-Fs/L),P1(3,1:L/2))
title('300HZ傅里叶变换')视图效果
5、正弦波相位
1)正弦波傅里叶变换
代码
Fs = 100;
t = 0:1/Fs:1-1/Fs;
x = cos(2*pi*15*t - pi/4) + cos(2*pi*40*t + pi/2);
y = fft(x);
z = fftshift(y);
ly = length(y);
f = (-ly/2:ly/2-1)/ly*Fs;
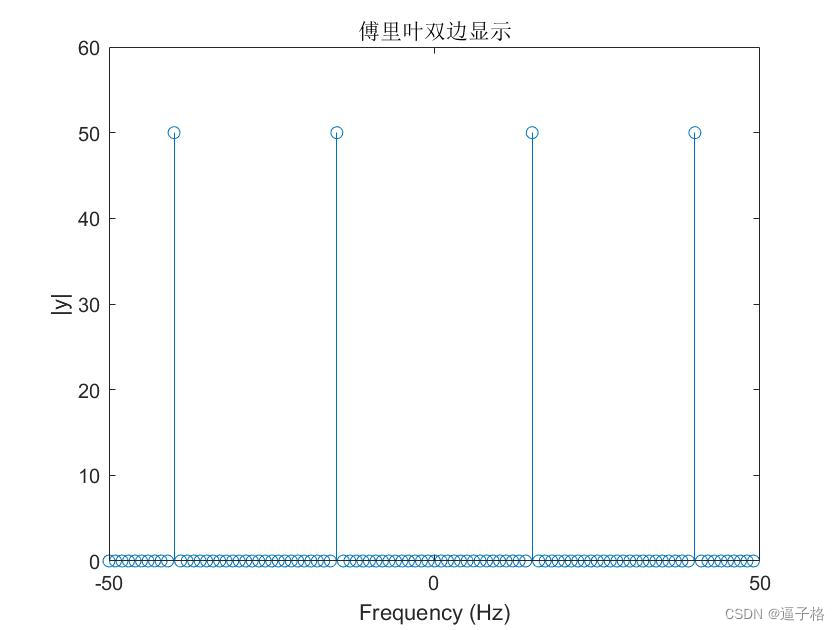
stem(f,abs(z))
title("傅里叶双边显示")
xlabel("Frequency (Hz)")
ylabel("|y|")视图效果
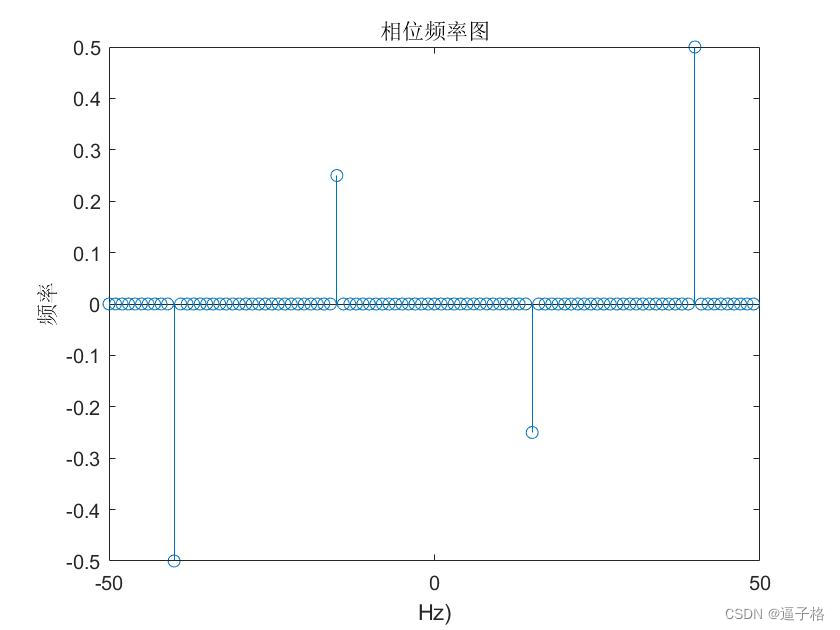
2)相位获取
代码
1tol = 1e-6;
z(abs(z) < tol) = 0;
theta = angle(z);
stem(f,theta/pi)
title("相位频率图")
xlabel("Hz)")
ylabel("频率")视图效果