小波散射变换的目的在于获取第一层次的特征信息,即免疫平移、轻微形变的信息。而低通的滤波器能够获取输入信号的概貌,获取反映其整体大尺度特征的信息,以图像为例,由低通滤波器选取的信号对于图像的平移、伸缩、旋转等局部变化有良好的不变性。因此,小波散射变换获取了这一部分的信息。
相应的,高频部分的信号则对于信号的平移、伸缩、轻微形变类的变化具有协变性。换而言之,带通滤波器选取的信号成分受平移、伸缩、旋转等变化的影响较大,越是高频处的滤波选取越易受这些变化的影响。高频信息中包含着对提取共性特征不利的成分。但是,仅获取低频信息就意味着把包含重要信息成分的高频部分丢弃掉,这对于特征提取来说是一种损失。可以认为,散射变换最重要的目的就是在获取高频信息的同时,丢弃掉其对平移、形变敏感的部分。散射变化对此采取了如下的形式:

总的来说,小波散射变换的形式可以归结为,对信号做尺度不同的小波变换,对其进行取模,继而对变换结果做一个低通滤波,所得即是所提取的特征。从数学上的理解来看,由于同一小波的正交特性,不同特征间应是不具有相关性,每一个各代表了图像一部分的特征信息,所有层特征的组合即可认为是散射网络从中获取的特征之和。不同于卷积神经网络,散射网络每一层的特征提取器是复数个而非单一特征提取器,且每一层用的都是同一套特征提取器。这与其他的多层架构网络也不同。同时,不同于卷积神经网络只用最后一层的输出,即将经过所有特征提取器的信息来作为最后的特征输出,散射网络在所有层都有输出,最后将这些输出的特征组合来作为总的输出特征。最后也是最显著的一点,散射网络不是前馈式网络,它的所有卷积核都是预先选定的,换句话说,在对图像进行特征提取之前,它所要提取的目标特征就是确定的。这样做的好处在于,省略了训练的过程,可以根据理论提取到具有目标性质的特征,计算量大大减少的同时也具有了结果的理论解释,这是一种介于传统图像识别和深度学习之间的算法。
鉴于此,采用小波时间散射变换对一维时间序列信号进行分析,运行环境为MATLAB 2021B。
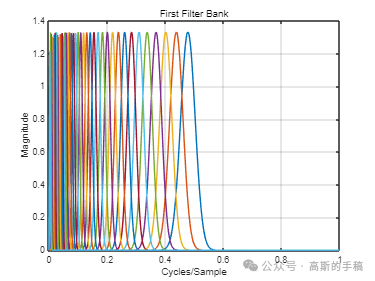



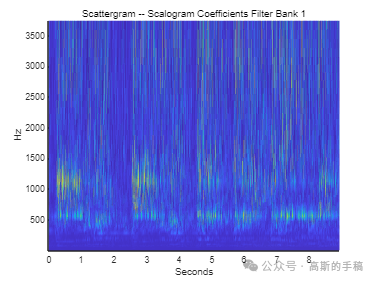
for nl = 1:numel(fb)
phift = self.filters{fb(nl)}.phift;
psift = self.filters{fb(nl)}.psift;
% Obtain wavelet filters
positiveMag2Psift = psift.*conj(psift);
negativeMag2Psift = circshift(flip(positiveMag2Psift),1);
positiveMag2Psift = sum(positiveMag2Psift,2);
negativeMag2Psift = sum(negativeMag2Psift,2);
Mag2Phift = phift.*phift;
lpsum(:,nl) = Mag2Phift+1/2*(positiveMag2Psift+negativeMag2Psift);
完整代码https://mbd.pub/o/bread/mbd-ZJyYmZxq
end工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。