🔥🔥 欢迎来到小林的博客!!
🛰️博客主页:✈️小林爱敲代码
🛰️欢迎关注:👍点赞🙌收藏✍️留言
这篇文章给大家带来一些关于二叉树的oj题
每日一句: 立身以立学为先,立学以读书为本。
目录
- 💖1. 二叉树的分层遍历
- 💖2. 二叉树的分层遍历(逆)
- 💖3. 找2个节点的最近公共祖先
- 💖4. 二叉搜索树与双向链表
- 💖5. 从前序与中序遍历序列构造二叉树
- 💖6.从中序与后序遍历序列构造二叉树
- 总结🥳:
💖1. 二叉树的分层遍历
题目:
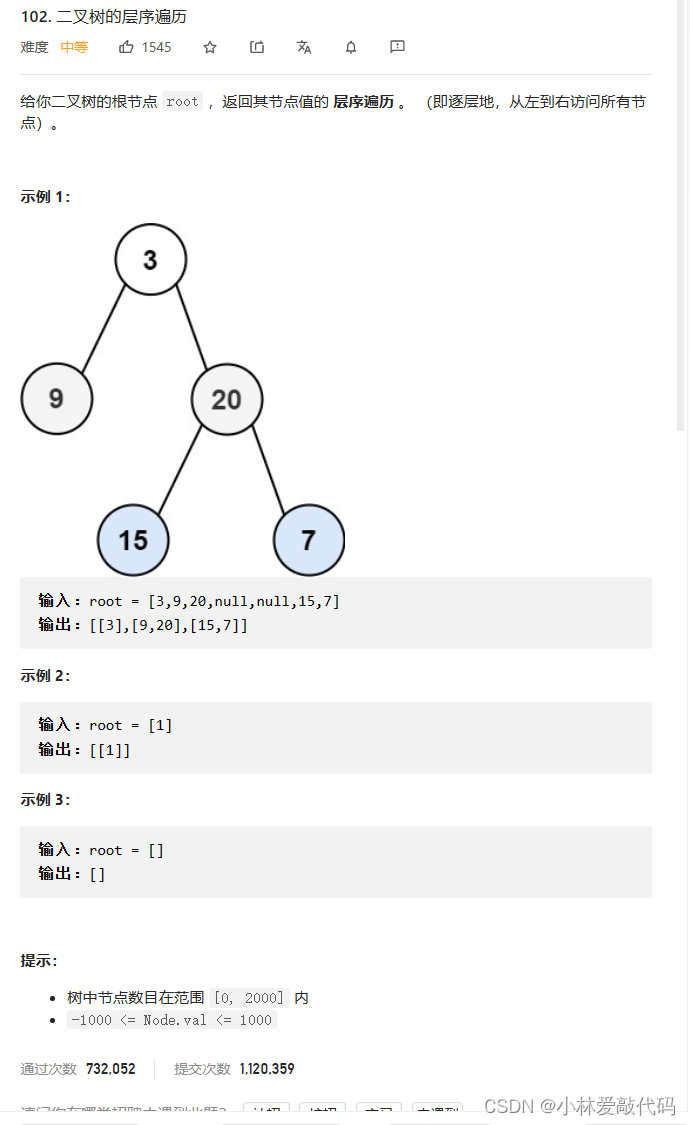
解题思路:
用一个队列入数据,并且用一个变量leavesSize 来记录当前一层的数据个数。然后用数组存储当前这一层的数据。再把这个数组添加到数组中。

代码:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
vector<vector<int>> vv;
int leavesSiez = 1;
//入根节点,根节点为空说明是空树
if(root)
q.push(root);
//队列为空结束循环
while(!q.empty())
{
vector<int> v;
while(leavesSiez--)
{
TreeNode* front = q.front();
//放进数组
v.push_back(front->val);
//弹出队头数据
q.pop();
//左右子树不为空则入队列
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
//更新层数节点数量
leavesSiez = q.size();
vv.push_back(v);
}
return vv;
}
题目链接:https://leetcode.cn/problems/binary-tree-level-order-traversal/submissions/
💖2. 二叉树的分层遍历(逆)
题目:
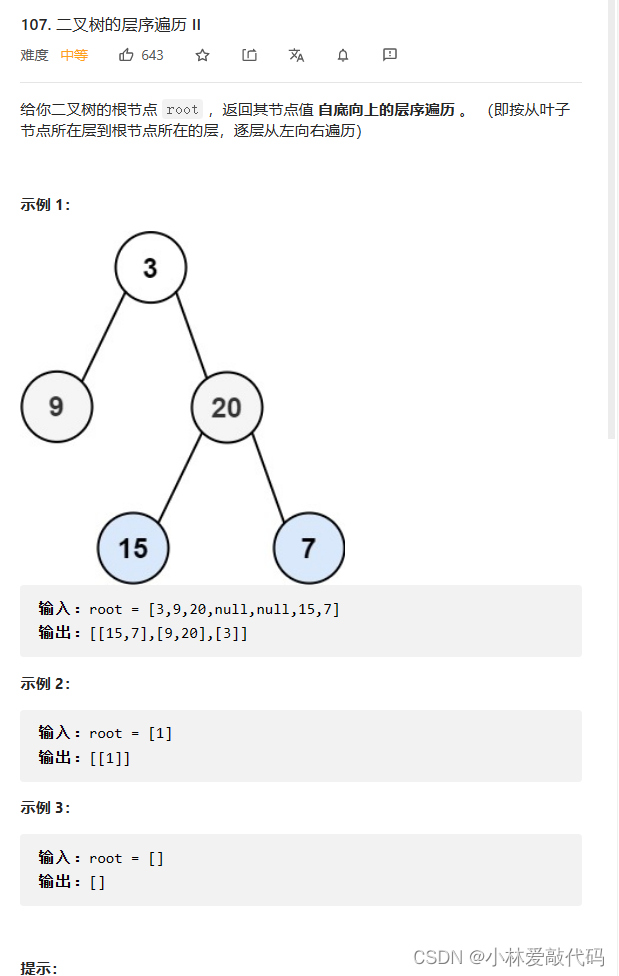
思路: 和上一题一样,只不过把最后返回的数组逆置即可。
代码:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
vector<vector<int>> vv;
int leavesSiez = 1;
//入根节点,根节点为空说明是空树
if(root)
q.push(root);
//队列为空结束循环
while(!q.empty())
{
vector<int> v;
while(leavesSiez--)
{
TreeNode* front = q.front();
//放进数组
v.push_back(front->val);
//弹出队头数据
q.pop();
//左右子树不为空则入队列
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
//更新层数节点数量
leavesSiez = q.size();
vv.push_back(v);
}
//数组逆置
reverse(vv.begin(),vv.end());
return vv;
}
题目链接:https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/
💖3. 找2个节点的最近公共祖先
题目:
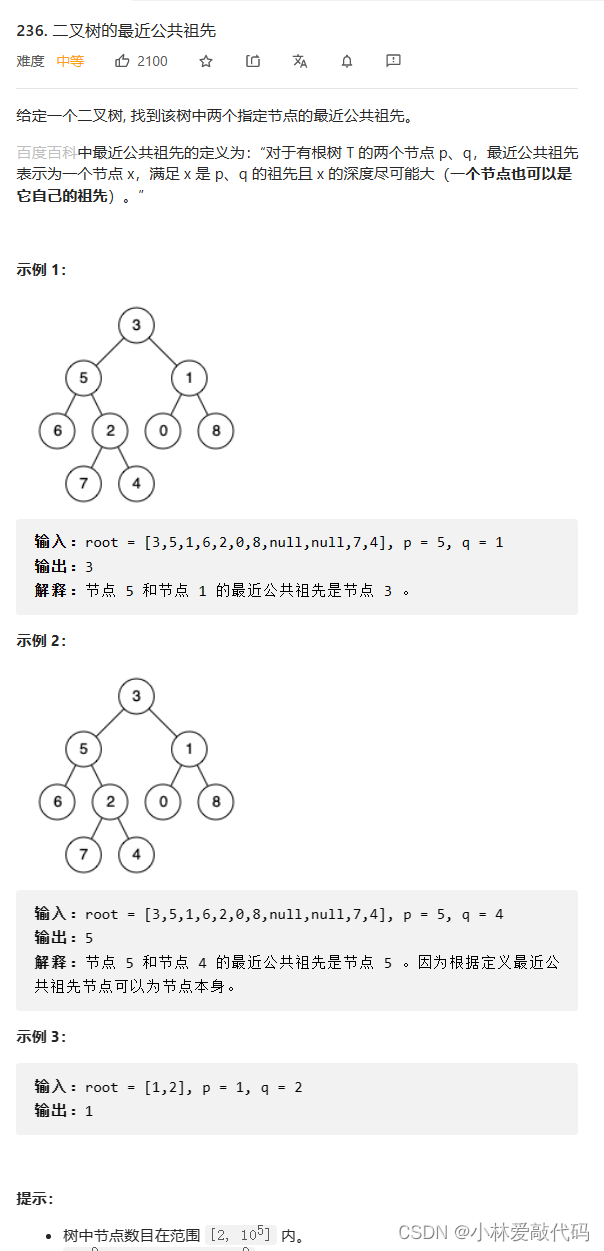
解题思路:用两个栈来保存2个节点的路径。随后会产生一大一小的两个栈,使大的栈和小的栈一样大后,同时pop比较节点地址。
我们可以分次查找,第一次找p的地址,第二次找q的地址。而查找的时候,一进去就让数据入栈,随后把该节点看成一棵树,如果这棵树里面没有找到要查找的节点,那么就会pop掉入栈的数据。如果找到了,返回true。
假设我们要找 6和7的最近公共父节点。
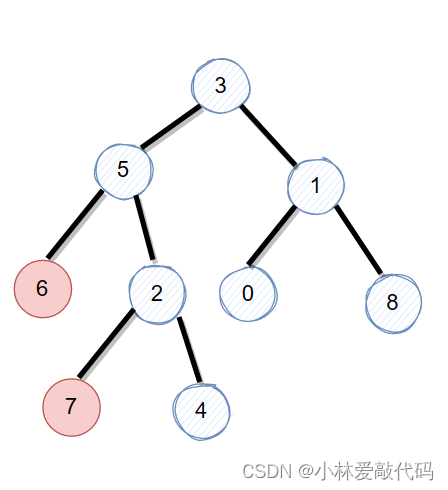
第一次查找,先遍历二叉树,去查找6的节点

第二次查找,遍历二叉树,查找7的节点。

随后我们得到了stack1和stack2两个栈,那么我们让长度长的那个栈pop,直到pop到两个栈一样大时,再同时pop。

2个栈栈顶节点相等时,随便返回一个即可。
代码:
bool FindNode(TreeNode* root,TreeNode* x,stack<TreeNode*>& stack)
{
//如果root为空,说明没找到,返回flase
if(root == nullptr)
return false;
//节点入栈,保存路径
stack.push(root);
//如果找到了,返回true
if(root == x)
return true;
//递归找左子树,如果有返回true的,说明找到了,就返回true,没找到则继续找右子树
if(FindNode(root->left,x,stack))
return true;
//递归找右子树
if(FindNode(root->right,x,stack))
return true;
//左右子树都没找到,说明这棵树没有要找的节点,那么pop掉刚开始push进来的根节点
stack.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> stack1;
stack<TreeNode*> stack2;
//找p节点
FindNode(root,p,stack1);
//找q节点
FindNode(root,q,stack2);
//使两个栈长度一样
while(stack1.size() != stack2.size())
{
if(stack1.size() > stack2.size())
stack1.pop();
else
stack2.pop();
}
//到这里两个栈一样大了,那么同时出数据
while(stack1.top() != stack2.top())
{
stack1.pop();
stack2.pop();
}
//随便返回一个
return stack1.top();
}
题目链接:https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/submissions/
💖4. 二叉搜索树与双向链表
题目描述:

解题思路:首先,这个二叉树是被中序遍历的。而在遍历的过程中,我们需要保存前一个节点。这样才能相互链接。

如图所示,按照图中步骤,即可实现链接过程。
代码:
void InOrder(TreeNode* cru,TreeNode*& prev)
{
//中序遍历
if(cru == nullptr)
return;
InOrder(cru->left,prev);
//链接操作
cru->left = prev;
if(prev)
prev->right = cru;
//prev到cru的位置上
prev = cru;
InOrder(cru->right,prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
TreeNode* prve = nullptr;
InOrder(pRootOfTree,prve);
TreeNode* head = pRootOfTree;
//找链表头节点
while(head && head->left)
{
head = head->left;
}
return head;
}
题目链接:https://www.nowcoder.com/practice/947f6eb80d944a84850b0538bf0ec3a5?tpId=13&&tqId=11179&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking
💖5. 从前序与中序遍历序列构造二叉树
题目:
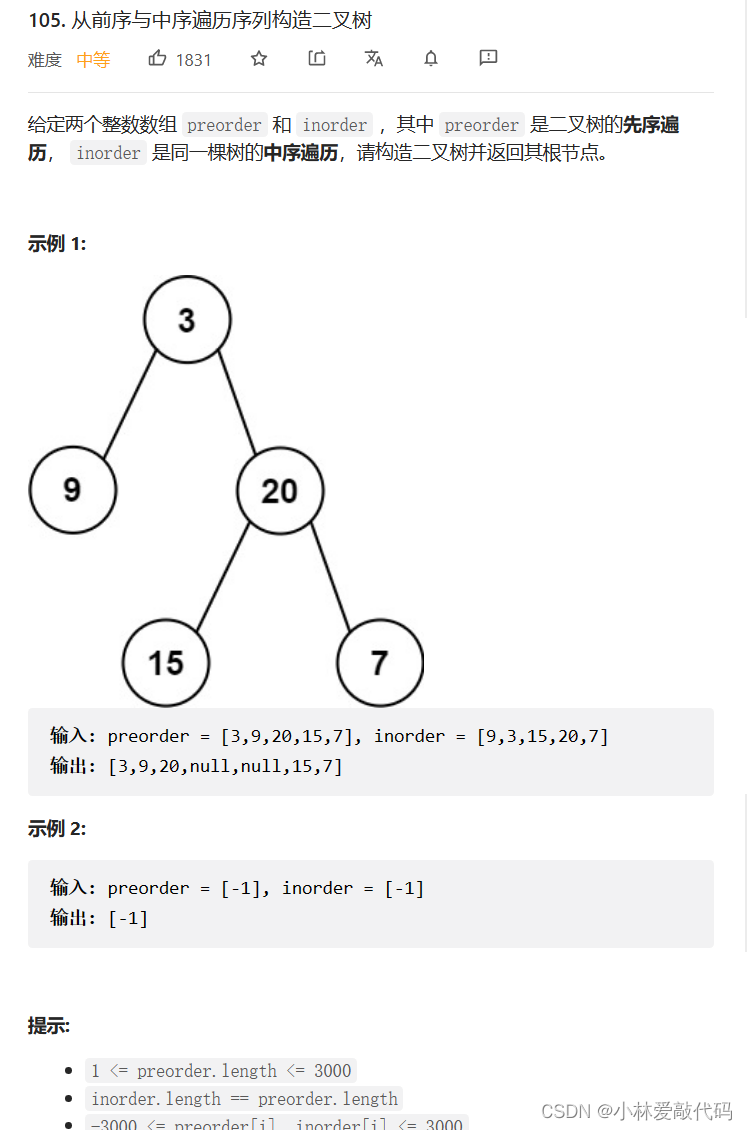
解题思路:用begini 和 endi 变量作为一颗树的区间,而prei则是树的根节点,因为是前序遍历。所以我们在前序数组中找根,在中序数组里找根的子树区间。

代码:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int prei = 0;
return _buildTree(preorder,inorder,prei,0,inorder.size()-1);
}
TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int& prei,int begini,int endi) {
//如果begin大于endi,说明没有节点了。
if(begini > endi)
return nullptr;
//创建根节点
TreeNode* root = new TreeNode(preorder[prei]);
//找到根节点在中序数组里的下标
int rooti = 0;
while(inorder[rooti] != root->val )
{
rooti++;
}
//prei++代表下一颗树的根,也代表这棵树的节点
prei++;
//begini - rooti -1 是root的左树区间,rooti+1 - endi是root的右树区间
root->left = _buildTree(preorder,inorder,prei,begini,rooti-1);
root->right = _buildTree(preorder,inorder,prei,rooti+1,endi);
return root;
}
题目链接:https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/submissions/
💖6.从中序与后序遍历序列构造二叉树
题目:
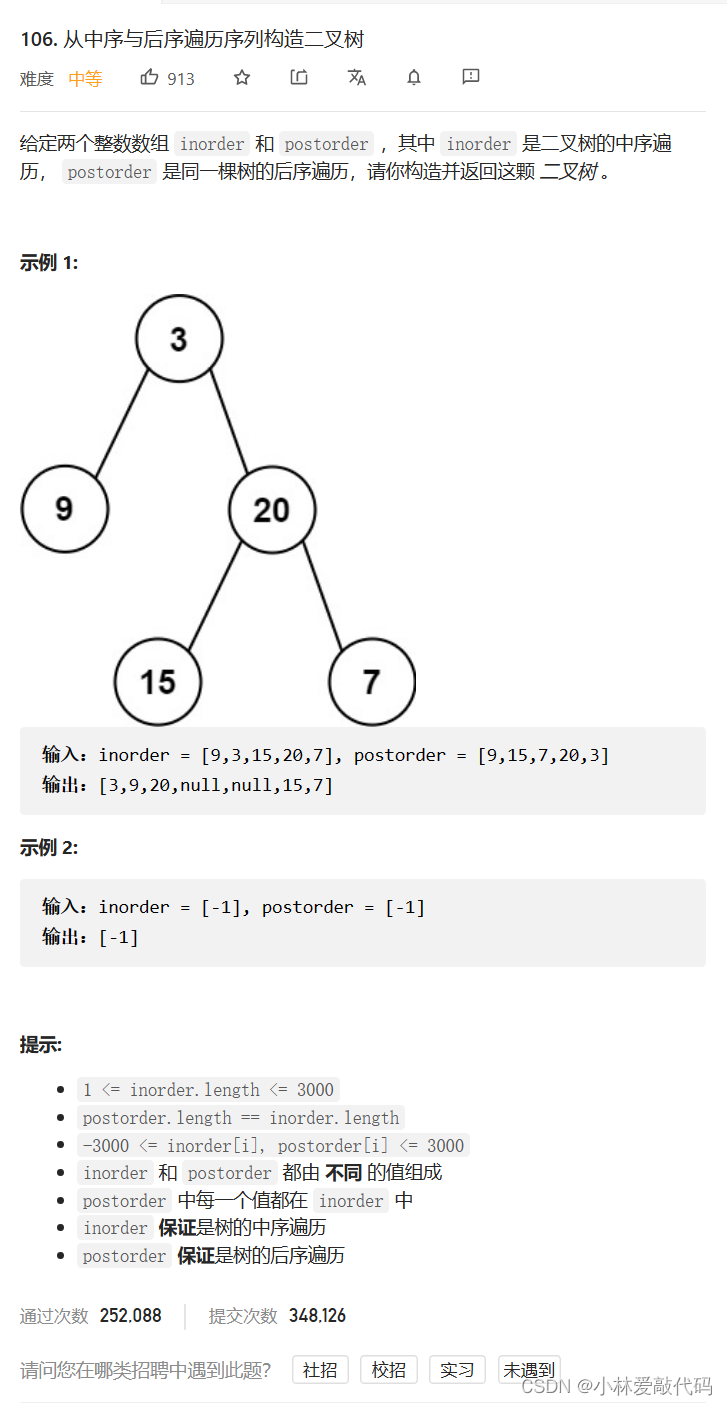
解题思路:
中序与后序构造前序二叉树,和前序与中旬构造后序二叉树差不多。思想都是一致的,有3个变量,posti控制树的根,begini和endi控制树的区间。前序数组的第一个元素就是树的根,那么后序数组的最后一个元素就是它的根。从后往前需要注意点的就是,必须要先连接右树,再连左树,否则posti的值会对不上。

代码:
TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder,int& posti,int begini,int endi) {
//左区间比右区间大, 说明没有节点了
if(begini > endi)
return nullptr;
//创建根节点
TreeNode* root = new TreeNode(postorder[posti]);
int rooti = 0 ;
//找到根节点在中序数组的下标
while(inorder[rooti] != root->val)
{
rooti++;
}
posti--;
//先链接右节点,后序遍历是左,右,根。反过来就是 根 右 左
root->right = _buildTree(inorder,postorder,posti,rooti+1,endi);
root->left = _buildTree(inorder,postorder,posti,begini,rooti-1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int posti = postorder.size() - 1;
return _buildTree(inorder,postorder,posti,0, postorder.size() - 1);
}
题目链接:https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
总结🥳:
💦💦如果有写的有什么不好的地方,希望大家指证出来,我会不断的改正自己的错误。💯💯如果感觉写的还可以,可以点赞三连一波哦~🍸🍸后续会持续为大家更新.
🔥🔥你们的支持是我最大的动力,希望在往后的日子里,我们大家一起进步!!!🔥🔥


![[JavaEE]线程池](https://img-blog.csdnimg.cn/5106466fd66245a5b53b1f687a282933.png)