首先都是线性的,线性包括顺序和链式,栈和队都可以用两种方式实现。栈只能存于栈顶取于栈顶,队列先进先出,因此存取点是固定的。
首先都是线性的,线性包括顺序和链式,栈和队都可以用两种方式实现。栈只能存于栈顶取于栈顶,队列先进先出,因此存取点是固定的。
 函数栈帧创建原理
函数栈帧创建原理
 画图即可。
画图即可。
 A.显然不行,5如果第一个出来说明5是最后一个进的,5如果下面就是1,说明234都已经不在栈内了,才能轮到1,但是选项中1后面竟然还跟着234,说明不对
A.显然不行,5如果第一个出来说明5是最后一个进的,5如果下面就是1,说明234都已经不在栈内了,才能轮到1,但是选项中1后面竟然还跟着234,说明不对
B.4第一个5第二个都合理,不合理的是132
C.改成43215就是对的了
D.先入栈123,再出栈321,在入栈45,再出栈54
 A.入栈abcde,出栈edcba。
A.入栈abcde,出栈edcba。
B.入栈abcd,出栈d;入栈e,出栈e;出栈cba。
C.a不可能再b前面出栈
D.每个元素一入马上出。
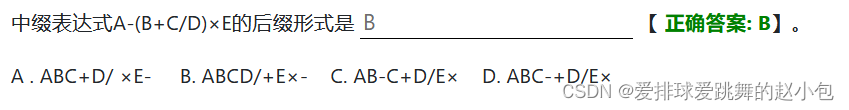
中缀表达式转后缀表达式步骤:
1、遇到操作数,直接输出
2、遇到运算符,若该运算符的优先级大于栈顶运算符的优先级,则压栈;若小于等于栈顶运算符,将栈顶运算符输出,再与新的栈顶元素比较,按照同样的处理方式,直到该运算符的优先级大于栈顶元素或者空集或者左括号,压栈;若栈顶是左括号,入栈。
3、遇到左括号,压栈。
4、遇到右括号,栈顶运算符出栈并依次输出,直至遇见左括号,左括号出栈但不输出。
 p的后指针指向q;
p的后指针指向q;
p的前指针指向q的前指针;
q的前指针指向p;
p的前指针的后指针等于p。

A.栈空不行B.栈满不行D.队满不行。
关键在于顺序存储,顺序存储就是数组,而数组是静态的,容量优先。链式就不存在这个问题。
 那这个很简单啦,去打印店,先到的先打印,后到的后打印。
那这个很简单啦,去打印店,先到的先打印,后到的后打印。
 入队:
入队:
rear=(rear+1)%length;
Queue[rear]=x;(要插入的元素)
count++;
出队:
count--;
输出Queue[front];
front=(front+1)%length;
 理论上,都可行,但是他是队列,所以只能进行出队入队操作。
理论上,都可行,但是他是队列,所以只能进行出队入队操作。
 入栈abcd(4),出栈d(3);入栈ef(5),出栈fe(3);出栈c(2);入栈gh(4),出栈hg(2);出栈ba(0);
入栈abcd(4),出栈d(3);入栈ef(5),出栈fe(3);出栈c(2);入栈gh(4),出栈hg(2);出栈ba(0);

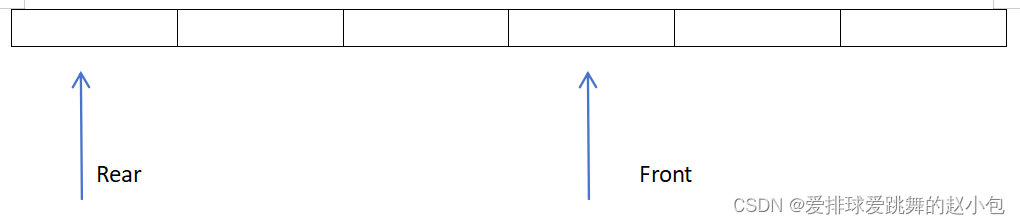
删一个:
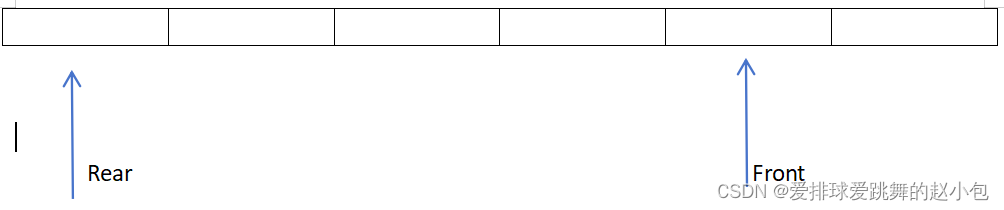 加两个:
加两个:
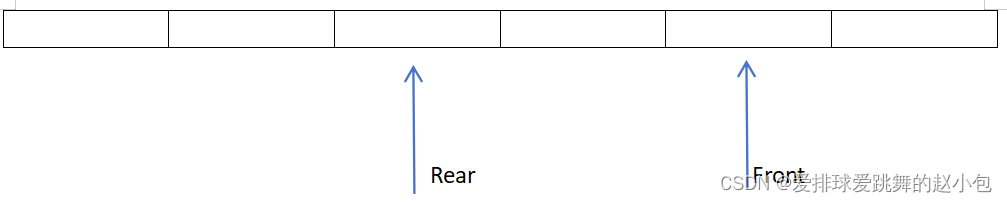
答案2,4
 while(s[j])j++;是把j指向了字符串末端,也就是‘\0’的位置。
while(s[j])j++;是把j指向了字符串末端,也就是‘\0’的位置。
for循环中–j又让j指向了字符串的最后一个有效字符。
然后不断头尾对比是否一致。
如果字符串长度是奇数,那么如果对称,则最后i=j,如果是偶数,则i>j;
如果i<j,说明中间有一对不一样,导致for循环终止,则返回零。
 1234
1234
1342
S X S S X S X X
 第一个出栈的是30,说明之前没有元素出栈,全都入栈了,那么接下来的出栈顺序就只能是依次输出了。p10=30-10+1=21。
第一个出栈的是30,说明之前没有元素出栈,全都入栈了,那么接下来的出栈顺序就只能是依次输出了。p10=30-10+1=21。
 pop两次,第一次b,第二次c。
pop两次,第一次b,第二次c。
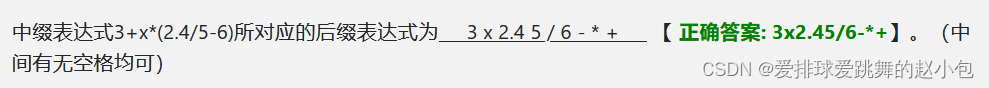 和上面一道题类似。
和上面一道题类似。
 画图解决一切。
画图解决一切。
 每次进行一个运算符的运算,都带上一个括号比较好!
每次进行一个运算符的运算,都带上一个括号比较好!
感觉今天的文写的很水,但是确实把这个基础题复习到了。明天把这部分的编程题复习一下然后开始复习二叉树!!