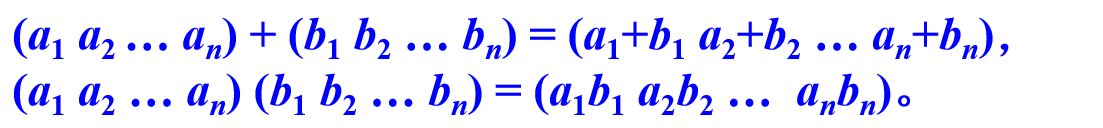4.1 环与子环 (理解)
4.2 整环、除环、域 (熟练)
4.3 环的同态、理想 (掌握)
4.1 环与子环
定义:设R是一非空集合,在R上定义了加法和乘法两种代数运算, 分别记为a+b和ab.如果R具有如下性质:
1) R对于加法是一个交换群;
2) R对于乘法是封闭的;
3) 乘法满足结合律,即对于任意a,b,c∈R,有 a(bc) = (ab)c;
4) 分配律成立,即对于任意a,b,c∈R,有 a(b+c) = ab+ac,(b+c)a = ba+ca; 则称R为一个环。
如果环R关于乘法还满足交换律,即对于任意a,b∈R,总有ab = ba,则称R为交换环。
例:全体有理数、全体实数、全体复数和全体整数集合对于普通的加法和乘法构成交换环,其中全体整数集合Z构成的环比较重要,称为整数环。
例:模m的剩余类集合
上的乘法如下:
,则剩余类集合对于剩余类加法和乘法构成一个交换环,称为模m剩余类环。
零元:加法群的单位元称为零元,记为0。
负元:元素的加法逆元称为负元,记为-a。
单位元:乘法单位元称为单位元,记为1。
逆元:乘法逆元,记为a^(-1)。
环不一定存在单位元和逆元。但如果环中存在单位元和逆元,则它们一定是唯一的。
有理数、实数、复数和整数环都有单位元1;有理数、实数和复数环的非零元都有逆元; 但整数环Z除±1外,其他元素都没有逆元。
环的计算规则:
假设R是一个环,a,b,c∈R
1) 0+a = a+0 = a
2) a+(-b) = a-b
3) (-a)+a = a-a = 0
4) - (-a) = a
5) 如果a+b = c,则 b = c-a
6) -(a+b) = -a-b,-(a-b) = -a +b
7) 对于任意正整数n,有 (-n)a = - (na),0a = 0
8) 对于任意整数n,m,有 (n+m)a = na+ma,n(ma) = (nm)a,n(a+b) = na+nb
9) 对于任意正整数n,m,有
注意在R中一般不能定义a^0和a^(-n),因为环中不一定存在单位元和逆元。
10) (a-b)c = ac-bc,c(a-b) = ca-cb
11) 0a = a0 = 0(这里的0是R的零元)
12) (-a)b = a(-b) = -ab,(-a)(-b) = ab
13) 
更一般地,
或表示为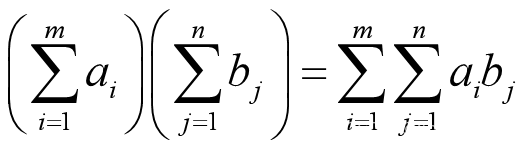
14) 对于任意整数n,有 (na)b = a(nb) = n(ab)
定义:如果在环里 a≠0,b≠0,但 ab = 0, 则称a是这个环的一个左零因子,b是这个环的一个右零因子。
(1)交换环里每个左零因子同时又是右零因子。如果一个左零因子同时又是右零因子,则称为零因子。
(2) 非交换环里的左零因子或右零因子也可能成为零因子。
例:模12剩余类环中的全部零因子是:
一个环里可以没有任何零因子。例如整数环Z。 在没有任何零因子存在的环里,如果ab=0,则必有a=0或b=0。
例:当m是素数时,模m剩余类环无零因子。
定理:在没有任何零因子的环里消去律成立,即如果a≠0,则 ab = ac⇒b=c,ba=ca⇒b=c。反之,如果上面的消去律中的任一个成立,则环里没有零因子。
定义:如果一个环R的子集S对于R中的运算也构成环,则称S为R的子环,R为S的扩环。
子集S构成一个子环的充要条件:
1) S对于加法构成一个子群。
2) S对于乘法封闭。
判定:对于任意a,b∈S,有 a-b∈S,ab∈S
例:全体偶数集合构成一个环,是整数环Z的子环,而Z是它的扩环。
例:整数环Z中任意整数的倍数nZ={rn|r∈Z}是Z的子环。
4.2 整环、除环、域
定义:如果一个环R满足下列条件:
1) 是交换环;
2) 存在单位元,且1≠0(等价于A≠{0});
3)没有零因子。
则R称为整环。
如整数环、全体有理数环、全体实数环和全体复数环都是整环。
定义:如果一个环R存在非零元,而且全体非零元构成一个乘法群,则R称为除环。
除环的来历是由于每个非零元都有逆元,可以做“除法”。
定义:一个交换除环称为一个域。
该定义等价于如果一个环F存在非零元,而且全体非零元构成 一个乘法交换群,则F称为一个域。
例:全体有理数、全体实数和全体复数对于普通的加法和乘法都是除环,且是可交换的除环。故他们是域,统称为 数域。但整数环由于不是每个元素都有逆元,所以不是除环。
例:当p是素数时,模p剩余类集合对于剩余类加法和乘法构成一个域,记为GF(p) 。
已证明GF(p)是一个模p剩余类环,是交换环,现在证明GF(p)非零元集合,GF*(p)构成一乘法交换群,从而GF(p)是一个域。GF(p)非零元集合GF*(p),
1) 乘法结合律和交换律显然满足。
2) 任意0<i,j≤p-1,由于(p, i) = 1,(p, j) = 1,则(p , ij) = 1,ij≠0(mod p),于是乘法封闭。
3)是乘法单位元。
4) 对于任意
∈GF*(p),与GF*(p)中的每个元素相乘得
这p-1个结果两两不同。否则假设如果
p|(ia-ib) = i(a-b)。 而(p, i) = 1,则只有p|(a-b),这与
矛盾。
上述的p-1个不同的结果跑遍GF*(p)的全部元素,当然也包括单位元
,所以
存在逆元。故GF*(p)是乘法交换群。GF(p)是域。
当p不是素数时,它可以分解为两个或更多的小于它的数的乘积,故模m剩余类环有零因子,不可能成为域。
如果从群出发,则一个集合F是一个域应该:
1) 构成加法交换群;
2) 非零元构成乘法交换群;
3) 满足分配律。
域、除环和环的关系如下图所示。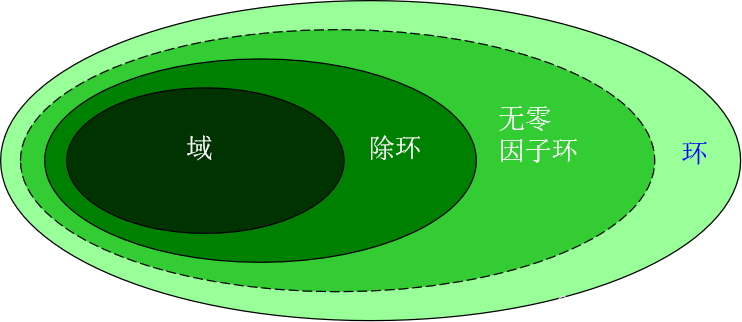
有限除环:元素个数有限的除环。
有限域:元素个数有限的域。
例:GF(p)是有限域,且是最简单的有限域。除环和域同样有子除环和子域的概念。
子除环:如果一个除环的子集也是除环;
子域:如果一个域的子集也是域。
一个除环的一个子集S构成一个子除环的条件是:
1) S包含非零元
2) 对于任意a,b∈S,有a-b∈S;
3) 对于任意a,b∈S,b≠0,有ab^(-1)∈S
环的同态、理想
定义:R和R’是两个环,如果存在R到R’的一个映射f,加法和乘法都在f下得到保持,即对于任意a,b∈R,有 f(a+b) = f(a)+f(b), f(ab) = f(a)f(b),则称f是R到R’的同态映射,或简称同态。
如果f是单射,则称f是单同态。
如果f是满射,则称f是满同态。
如果f是一一映射,则称f是同构,此时称R和R’同构,并用R≌R’表示。
例:设R是一个环,Rn是R上的n维向量,即
定义R^n上的加法和乘法如下:
则R^n构成一个环.定义R^n→R的映射 f((a1 a2 … an)) = a1。f是Rn到R的满同态。
定理:f是环R到R’的同态,则有
1) f(0) = 0’(0’是R’的零元)
2) 对于任意 a∈R,有 f(-a) = -f(a)。
3) 如果f是环R到R’的满同态,且R有单位元,则R’也有单位元,且f(1) = 1’(1’是R’的单位元)。
4) 如果f是环R到R’的满同态,且R有单位元,而且a∈R可逆,则 f(a)在R’中可逆,且f(a)-1=f(a-1)。
5)如果f是环R到R’的满同态, 且R是交换环,则R’也是交换环。
例: 整数环R到模m剩余类环存在下列同态f:i∈Z,
Z没有零因子,但m不是素数时,模m剩余类环却有零因子。
没有零因子这个性质在同态下不一定保持。
定理:如果两个环R≌R’,则
1) 如果R是整环,R’也是整环;
2) 如果R是除环,R’也是除环;
3) 如果R是域,R’也是域。
环同态也有核的概念。f是环R到R’的同态,设0’是R’的零元,则f的核为![]() 。定理表明在同态f下,0的像是0’。除0外,还可能有其他元素的像是0’.因此|ker(f)| ≥ 1。但显然在单同态和同构下,ker(f) = {0}。
。定理表明在同态f下,0的像是0’。除0外,还可能有其他元素的像是0’.因此|ker(f)| ≥ 1。但显然在单同态和同构下,ker(f) = {0}。
1) ker(f)是R的加法群的一个子群;
2) f是单同态当且仅当ker(f) = {0}。ker(f)是否是一个子环,只需检查乘法在ker(f)中是否封闭。 如果a,b∈ker(f),那么f(ab) = f(a)f(b) = 0’。 则ab∈ker(f)。可见ker(f)是R的一个子环。
实际上对于任意r∈R和a∈ker(f),都有f(ra) = f(r)f(a) = 0’,f(ar) = f(a)f(r) = 0’, 即ra,ar∈ker(f)。这表明ker(f)是很特殊的一种子环。
定义:设I是环R的加法子群。如果对于任意r∈R和a∈I,都有 ra∈I, 则称I是R的一个左理想。如果对于任意r∈R和a∈I,都有 ar∈I, 则称I是R的一个右理想。当I同时是左理想和右理想时,称为理想。环同态的核就是理想。显然对于交换环,左理想、右理想和理想是相同的。
例:整数环Z中任意整数的倍数 mZ = {rm|r∈Z} 是Z的理想。
定理:环R的非空子集I是左理想的充要条件:对于任意a,b∈I和rR,有 a-b∈I,ra∈I. 对于右理想和理想也可以有类似的定理。
显然{0}是环R的理想,称为零理想;R也是R的理想,称为单位理想.
零理想和单位理想统称为平凡理想。平凡理想之外的理想称为真理想。
除环仅有平凡理想。理想这个概念对于除环和域没有什么意义。
定理:两个左理想的交是左理想,两个右理想的交是右理想,两个理想的交是理想。
推论:多个左理想的交是左理想,多个右理想的交是右理想,多个理想的交是理想
主理想与主理想整环
定义:设X是环R的非空子集,{I1,I2,…}是包含X的所有理 想,则称它们的交是由X生成的理想,记为(X).
X中的元素称为 (X)的生成元素:
当X是有限集时,称(X)是有限生成理想。
由一个元素生成的理想(a)称为主理想。
定义:如果一个整环上的理想都是主理想,则称为主理想整环。
例:整数环Z是主理想整环。