回归模型的算法性能评价

news2025/1/17 6:04:52

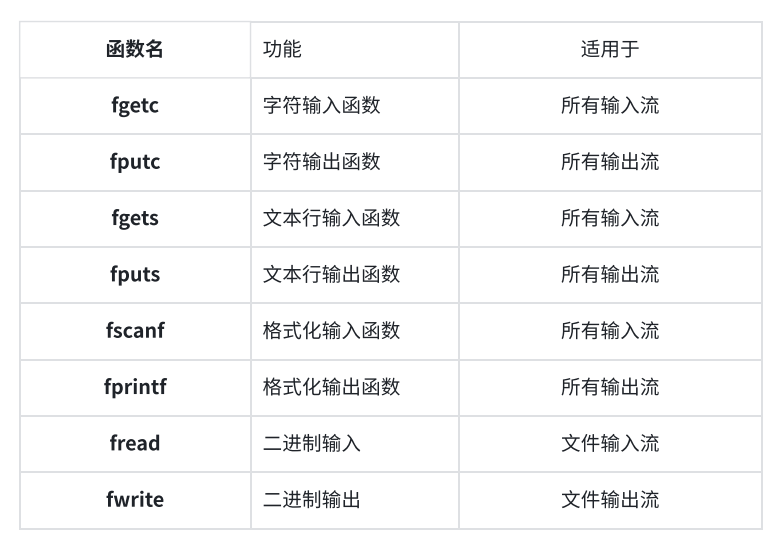
一、概述

在一般形式的回归问题中，会得到系列的预测值，它们与真实值（ground truth）的比较表征了模型的预测能力，为有效量化这种能力，常见的性能评价指标有平均绝对误差（MAE）、均方误差（MSE）、均方根误差（RMSE）、决定系数（R2）、可解释方差（EVS）等。值得一提的是，回归问题分单输出情形和多输出情形，在多输出情形下，可以对各维度结果进行平均计算或以不同的权重进行计算。

二、评价指标

1. 平均绝对误差（Mean Absolute Error，MAE）

MAE是计算预测值与真实值之差的绝对值之和，再求平均。表达式为

$MAE=\frac{1}{n}\sum_{i=1}^{n}{\left| y_i-\hat{y}_i \right|}$

其中， $y_i$ 为真实值， $\hat{y}_i$ 为预测值。

2. 均方误差（Mean Squared Error，MSE）

MSE是计算预测值与真实值之差的平方之和，再求平均。表达式为

$MSE=\frac{1}{n}\sum_{i=1}^{n}{\left( y_i-\hat{y}_i \right)^{2}}$

其中， $y_i$ 为真实值， $\hat{y}_i$ 为预测值。

3. 均方根误差（Root Mean Squared Error，RMSE）

RMSE是对MSE作开方处理。表达式为

$RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{\left( y_i-\hat{y}_i \right)^{2}}}$
其中， $y_i$ 为真实值， $\hat{y}_i$ 为预测值。

4. 决定系数（The Coefficient of Determination，R2）

R2表征自变量对因变量的可解释程度，从波动性的角度衡量了模型对数据的契合程度，取值范围通常为[0,1]。值越接近于1，性能越好；值越接近于0，性能越差。表达式为

$R^{2}=1-\frac{\sum_{i=1}^{n}{\left( y_i-\hat{y}_i \right)^{2}}}{\sum_{i=1}^{n}{\left( y_i-\bar{y}_i \right)^{2}}}$

其中， $\bar{y}=\frac{1}{n}\sum_{i=1}^{n}{y_i}$ ， $y_i$ 为真实值， $\hat{y}_i$ 为预测值。

5. 可解释方差（Explained Variance Score，EVS）

EVS是模型的解释方差得分，与决定系数R2作用一致，用以衡量从波动性角度解释模型对数据的契合程度，取值范围通常为[0,1]。值越接近于1，性能越好；值越接近于0，性能越差。表达式为
$EVS=1-\frac{Var\{y-\hat{y}\}}{Var\{y\}}$
其中， $y_i$ 为真实值， $\hat{y}_i$ 为预测值。

三、Python实现

import numpy as np
import sklearn.metrics as mr

## 单输出情形
y_true = [[4],
          [5],
          [6],
          [7]]

y_pred = [[3],
          [4.2],
          [5],
          [6.3]]

print('\n 单输出情形：')

print('平均绝对误差MAE：',mr.mean_absolute_error(y_true, y_pred))
print('均方误差MSE：',mr.mean_squared_error(y_true, y_pred))
print('均方根误差RMSE：',np.sqrt(mr.mean_squared_error(y_true, y_pred)))
print('R2：',mr.r2_score(y_true, y_pred))
print('可解释方差EVS：',mr.explained_variance_score(y_true, y_pred, sample_weight=None, multioutput='uniform_average'))

print('\n----------')

## 多输出情形
y_true = [[1, 2, 3],
          [3, 4, 5],
          [5, 6, 7]]

y_pred = [[1.2, 2, 3.6],
          [3.3, 4, 5.7],
          [5.4, 6, 7.8]]


print('\n 多输出情形：')
print('平均绝对误差MAE_平均：',mr.mean_absolute_error(y_true, y_pred))
print('均方误差MSE：',mr.mean_squared_error(y_true, y_pred))
print('均方根误差RMSE：',np.sqrt(mr.mean_squared_error(y_true, y_pred)))
print('R2: ', mr.r2_score(y_true, y_pred))
print('可解释方差EVS：',mr.explained_variance_score(y_true, y_pred, sample_weight=None, multioutput='uniform_average'))


'''
注：其中可加入multioutput参数属性，multioutput='raw_values'是按维度计算指标值；multioutput=[p1,p2...,pn]是加权计算指标值。如
平均绝对误差MAE_按维度：,mr.mean_absolute_error(y_true, y_pred,multioutput='raw_values')
平均绝对误差MAE_加权：,mr.mean_absolute_error(y_true, y_pred,multioutput=[0.25,0.3,0.45])
'''