1、通过存储 额外信息的方法来扩张一 种标准的数据结构,然后对这种数据结构,编写新的操作来支持所需的应用。因为添加的信息 必须要能被该数据结构上的常规操作更新和维护
2、通过扩张红黑树构造出的两种数据结构:14.1介绍 一种支持一般动态集合上 顺序统计操作的数据结构。可以快速地找到 一个集合中的第i小的数,或 给出一个指示元素在集合的全序中的位置。14.2节 抽象出数据结构的扩张过程,并给出一个简化红黑树扩张的定理。14.3节 使用这个定理来设计 一种用于维护区间(如时间区间)构成的动态集合的数据结构。给定 一个要查询的区间,能快速地找到 集合中一个与其重叠的区间
1、动态顺序统计
1、对于一个无序的集合,能够在O(n) 时间内 确定任何的顺序统计量;可以在 O(lgn) 时间内 确定任何的顺序统计量。还将看到 如何在 O(lgn) 时间内计算一个元素的秩,即它在集合线性序中的位置
2、一个顺序统计树T 只是简单地 在每个结点上 储存附加信息的一棵红黑树。在红黑树的结点x中,除了通常属性 x.key、x.color、x.p、x.left 和 x.right 之外,还包括一个属性 x.size。这个属性 包含了以x为根的子树(包括x本身)的(内)结点数,即这棵子树的大小。如果定义哨兵的大小为0,也就是 设置T.nil.size为0,则有等式:
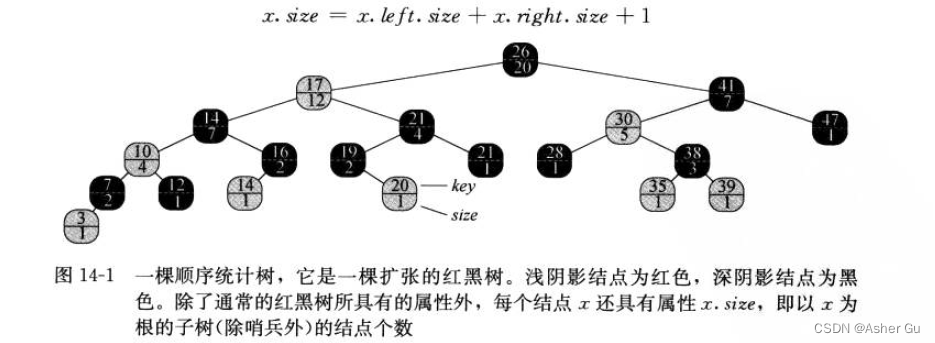
在一棵顺序统计树中,并不要求关键字各不相同。在有相等关键字的情况下,前面秩的定义 不再适合。为此,通过定义 一个元素的秩 为中序遍历时输出的位置,来消除 原顺序统计树 定义的不确定性
存储在黑色结点的关键字14的秩为5,存储在红色结点的关键字14的秩为6
3、过程OS-SELECT(x, i)返回一个指针,其指向以x为根的子树中 包含第i小关键字的结点

OS-SELECT的非递归版本:
OS-SELECT(x, i)
r = x.left.size + 1
while i != r
if i < r
x = x.left
else x = x.right
i = i - r
r = x.left.size + 1
return x
x.left.size + 1就是 以x为根的子树中结点x的秩。如果i > r,那么 第i小元素在x的右子树中。因为 对以x为根的子树 进行中序遍历时,其有 i-r 元素排在x的右子树之前,故在 以x为根的子树中 第i小元素就是 以x.right为根的子树中的 第 (i-r) 小元素
因为每次递归调用 都在顺序统计树中下降一层, OS-SELECT的总时间 与树的高度 成正比。又因为 该树是一棵红黑树,其高度为 O(lgn),其中n为树的结点数。 所以,对于n个元素的动态集合 OS-SELECT 的运行时间为 O(lgn)
4、确认一个元素的秩
给定 指向顺序统计树T中 结点x的指针,过程 OS-RANK 返回 对T中序遍历对应的线性序中x的位置

x的秩是在中序遍历次序排在x之前的结点数再加上1
循环不变式:
while循环 的每次迭代开始,r为以结点x为根的子树中 x.key的秩
初始化:第一次迭代之前,第1行置 r为以根的子树中x.key的秩。第2行置y=x,使得 首次执行第3行中的测试时,循环不变式为真
保持:在每一次while循环迭代的最后,都要置 y=y.p。如果r是在循环体开始 以y为根的子树中x.key的秩,那么 r是在循环结束时以y.p为根的子树中x.key的秩
考虑以y.p为根的子树,故要加上 以y的兄弟结点为根的子树 以中序遍历次序先于x的结点数,如果y.p也先于x, 则该计数还要加1
如果y是左孩子,y.p和y.p的右子树中的所有结点都不会先于x,r保 持不变;否则,y是右孩子,并且y.p和y.p左子树中的所有结点都先于x, 于是在第5行中,将当前的r值再加上y.p.left.size + 1
终止:当y=T.root时,循环终止,此时 以y为根的子树是一棵完整树。因此,r的值就是 这棵完整树中x.key的秩
给定元素的值的情况下 求秩
一个递归过程OS-KEY-RANK(T,k),以一棵顺序统计树T和一个关键字k作为输入,返回k在由T表示的动态集合中的秩。假设T的所有关键字都不相同
OS-KEY-RANK(T, k)
if k == T.key
return T.root.left.size + 1
elseif k < T.key
return OS-KEY-RANK(T.left, k)
else return T.root.left.size + 1 + OS-KEY-RANK(T.right, k)
5、对子树规模的维护
说明在不影响插入和删除橾作的渐近运行时间的前提下,如何维护子树规模
红黑树上的插入操作 包括两个阶段:第一阶段 从根开始沿树下降,将新结点插入 作为某个已有结点的孩子。第二阶段沿树上升,做一些变色和旋转操作 来保持红黑树性质
在第一阶段中为了维护子树的规模,对根至叶子路径上遇到的每一个结点x,都增加x.size属性。新增加结点的x.size为1,由于一条遍历路径上 共有 O(lgn) 个结点,所以维护 x.size 属性的额外代价为 O(lgn)
红黑树结构上的修改变 仅仅是旋转所致,旋转次数至多为2(上一节中的 情况2 + 情况3)。旋转是一种局部操作:它只会使得两个结点的size属性失效,而围绕旋转操作的链 就是与这两个结点关联
照图13.2节的LEFT-ROTATE(T,x)代码,增加下面两行:
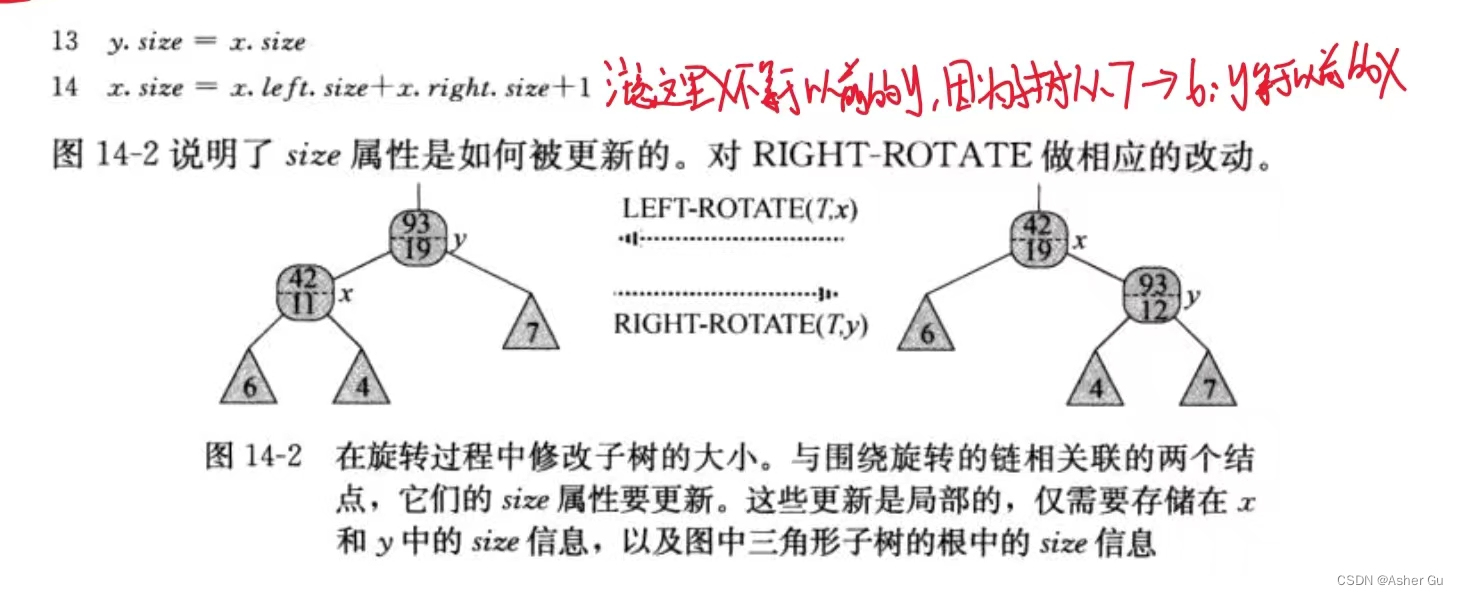
因为 在红黑树的插入过程中 至多进行两次旋转,所以 在第二阶段更新size属性 只需要O(1)的额外时间。因此,对于一个n个结点的顺序统计树插入元素 所需的总时间为O(lgn),从渐近意义上看,这与一般的红黑树是一样的
红黑树上的删除操作 也包括两个阶段:第一阶段 对搜索树进行操作,第二阶段 做至多三次旋转(根据上节 情况1转到3,情况2无旋转,情况3转情况4 就结束了),其他结构 均没有任何影响
第一阶段中,要么将结点y从树中删除,要么 将它在树上的位置上移。为了更新子树的规模,只需 遍历一条由结点y(从它在树中的原始位置开始)至根的简单路径,将沿路径上每个结点的size属性减1。因为在n个结点的红黑树中,这样一条路径长度为 O(lgn),所以第一阶段维护size属性所耗的额外时间为O(lgn)
第二阶段 采用与插入相同的方式来处理删除操作中的O(1)次旋转,所以 对在n个结点的顺序统计树中 进行插入和删除操作,包括维护size属性,都只需要O(lgn)时间
6、在OS-SELECT或OS-RANK中,注意到无论什么时候引用结点的size属性都是为了计算一个秩。相应地,假设每个结点都存储它在以自己为根的子树中的秩
1)在插入时维护这个信息:
红黑树上的插入操作包括两个阶段。第一阶段从根开始沿树下降,将新结点插入作为某个已有结点的孩子。第二阶段沿树上升,做一些变色和旋转操作来保持红黑树性质。
在第一阶段中 为了维护结点在以自己为根的子树中的秩,对由根至叶子的路径上遍历的每一个结点x,如果新结点将插入到它的左子树中,则它的rank加1,否则它的rank不变。由于一条遍历的路径上共有O ( lgn ) 个结点,故维护rank属性的额外代价为O ( lgn ) 。
在第二阶段,对红黑树结构上的改变仅仅是由旋转所致,旋转次数至多为2。此外,旋转是一种局部操作:它仅会使两个结点rank属性失效,而围绕旋转操作的链就是与这两个结点关联。参照13.2节的LEFT-ROTATE(T,x)代码,增加下面一行:
y.rank = y.rank + x.rank

2)在删除时维护这个信息:
红黑树上的删除操作 也包括两个阶段:第一阶段对搜索树进行操作,第二阶段做至多三次旋转,其他对结构没有任何影响。第一阶段中,要么将结点y从树中删除,要么将它在树中上移
为了更新结点在以自己为根的子树中的秩,我们只需要遍历一条由结点y(从它在树中的原始位置开始)至根的简单路径,如果当前结点是下个结点的左孩子,则下个结点的rank减1,否则下个结点的rank不变。因为在n个结点的红黑树中,这样一条路径的长度为 O(lgn),所以第一阶段维护rank属性 所耗费的额外时间为 O(lgn)。第二阶段 采用与插入相同的方式来处理删除操作中的 O(1) 次旋转。所以对有n个结点的顺序统计树 进行插入和删除操作,包括维护rank属性,都只需要 O(lgn) 的时间
2、如何扩张数据结构
1、通过 对数据结构进行扩张,来设计一种支持区间操作的数据结构。扩张一种数据结构可以分为4个步骤:
1)选择一种基础数据结构
2)确定基础数据结构中要维护的附加信息
3)检验基础数据结构上的各传统操作能否维护附加信息
4)设计新的操作
对于步骤1,选择红黑树作为基础数据结构。红黑树是一种合适的选择,这源于 它能有效地支持一些基于全序的动态集合操作, 如MINIMUM、MAXIMUM、SUCCESSOR和PREDECESSOR
对于步骤2,添加了size属性,在每个结点x中由size属性 存储了以x为根的子树的大小。仅用树中存储的关键字来实现 OS-SELECT和OS-RANK,但 却不能在O(lgn)运行时间内完成。有时,附加信息是指针变量值,而不是具体的数值
如:通过为结点增加指针的方式,在扩张的顺序统计树上,支持每一动态集合查询操作MINIMUM、MAXIMUM、SUCCESSOR和PREDECESSOR在最坏时间 O(1) 内完成。顺序统计树上的其他操作的渐进性能不应受影响:
- MINIMUM:用一个指针指向顺序统计树中的最小元素。每次向树中插入元素时与其进行比较,如果新插入的元素更小,则将MINIMUM指向新插入的元素,否则不做修改。如果删除MINIMUM,则将MINIMUM指向它的后继
- MAXIMUM:用一个指针指向顺序统计树中的最大元素。每次向树中插入元素时与其进行比较,如果新插入的元素更大,则将MAXIMUM指向新插入的元素,否则不做修改。如果删除MAXIMUM,则将MAXIMUM指向它的前驱
- SUCCESSOR:给每个结点增加指向后继的指针。每次向树中插入或删除结点时,根据插入或删除结点的父结点的SUCCESSOR,可以在时间内 O(1) 维护插入或删除结点的SUCCESSOR
- PREDECESSOR:给每个结点增加指向前驱的指针。每次向树中插入或删除结点时,根据插入或删除结点的父结点的PREDECESSOR,可以在时间内 O(1) 维护插入或删除结点的PREDECESSOR
2、红黑树扩张:设f是n个结点的红黑树T 扩张的属性,且假设对任一结点x,f的值 仅依赖于结点x、x.left和x.right的信息,还可能 包括x.left.f和x.right.f。那么,可以在 插入和删除操作期间对T的所有结点中的f值进行维护,并且不影响这两种操作的 O(lgn)渐近时间性能
证明:对树中某结点x的f属性的变动 只会影响到x的祖先。也就是说,修改x.f只需要更新x.p.f,改变x.p.f的值只需要更新x.p.p.f,如此沿树向上。一旦更新到T.root.f,就不再 对其他任何结点依赖于新值,于是过程结束。因为红黑树的高度为 O(lgn),所以改某结点的f属性要耗费O(lgn)时间
一个结点x插入到树T由两个阶段构成。第一阶段是 将x作为一个已有结点x.p 的孩子被插入。因为根据假设,x.f仅依赖于x本身的其他属性信息 和 x的子结点中的信息。在第二阶段期间. 树结构的仅有变动 来源于 旋转操作。由于 在一次旋转过程中 仅有两个结点发生变化. 所以每次旋转更新f属性的全部时间为 O(lgn)
与插入橾作类似,删除操作 也由两个阶段构成。在第一阶段中,当被删除的结点 从树中移除时,树发生变化。如果被删除的结点 当时有两个孩子,那么它的后继移入被删除结点的位置。这些变化 引起f的更新传播的代价 至多为O(lgn),因为 这些变化对树的修改是局部的。第二阶段 对红黑树的修复 至多需要三次旋转,且每次旋转 至多需要O(lgn)的时间就可完成f的更新传播。因此,和插入一样, 删除的总时间也是O(lgn)
在很多情况下,比如 维护顺序统计树的size属性,一次旋转后更新的代价为O(1),而并不是定理14.1中所给出的O(lgn)
3、能否 在不影响红黑树任何操作的渐近性能的前提下,将结点的黑高 作为树中结点的一个属性来维护?如何维护结点的深度
能在不影响红黑树任何操作的渐进性能的前提下,将结点的黑高作为树中结点的一个属性来维护:
插入和删除操作 只对从根结点到某一叶结点的路径上的结点(包括左右子树)进行修改,即 O(lgn) 个结点。修改每个结点的黑高 只需要 O(1) 时间。因此,总的修改时间为 O(lgn)
3、区间树
1、假设区间都是闭的,将集合推广至 开和半开区间上 是自然和直接的。区间便于表示 占用一定时间段的事件
我们可以把一个区间[t1, t2] 表示成一个对象,其中属性 i.low = t1 为低端点,属性 i.high = t2 为高端点
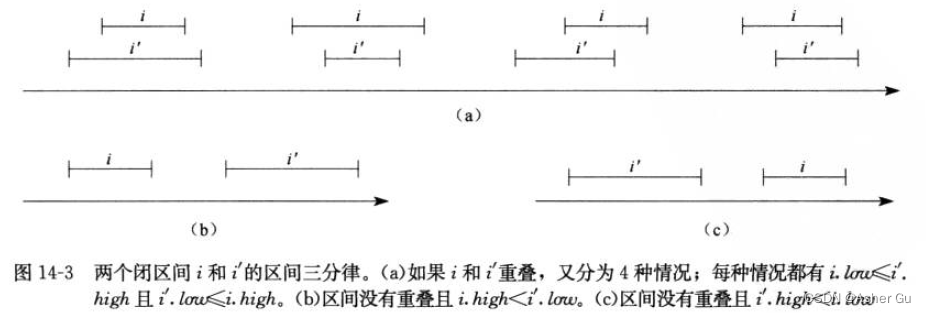
任何两个区间i和i’满足 区间三分律,即下面三条性质之一成立:
a. i和i’重叠。
b. i在i’的左边(也就是说i.high<i’.low)。
c. i在i’的右边(也就是说i.high<i’.low)。
2、区间树 是一种对动态集合进行维护的红黑树,其中每个元素x都包含一个区间x.int。区间树支持下列操作:
- INTERVAL-INSERT(T,x):将包含区间属性int的元素x插入到区间树T中
- INTERVAL-DELETE(T,x):从区间树T中删除元素x
- INTERVAL-SEARCH(T,i):返回一个指向区间树T中元素x的指针,使x.int与i重叠; 若此元素不存在,则返回T.nil
3、步骤1:基础数据结构
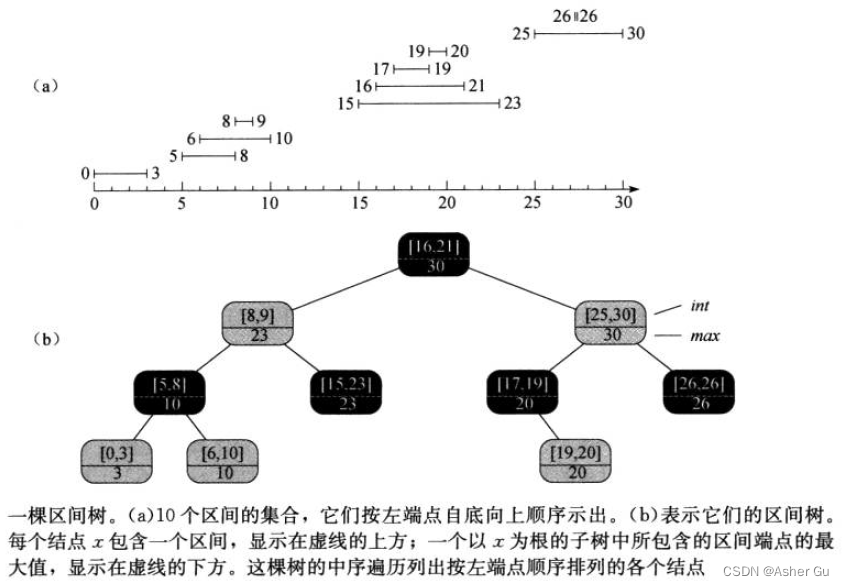
红黑树,其每个结点z包含一个区间属性x.int,且x的关键字为区间的低端点z.int.low。因此,该数据结构按中序遍历列出的 就是按低端点的次序排列的区间
步骤2:附加信息
每个结点x中除了 自身区间信息之外,还包含 一个值x.max,它是以x为根的子树中所有区间的端点的最大值
步骤3:对信息的维护
通过给定区间 x.int 和 结点x的子结点的最大值,可以确定x.max值:
x.max = max(x.int.high, x.left.max, x.right.max)
插入和删除操作的运行时间为O(lgn)。事实上,在一次旋转后,更新x.max仅需O(1)时间
步骤4:设计新的操作
仅需要 唯一的新操作 INTERVAL-SEARCH(T, i),用来找出树T中 与区间i重叠的那个结点
INTERVAL-SEARCH(T,i)
1 x = T.root
2 while x ≠ T.nil and i does not overlap x.int
3 if x.left ≠ T.nil and x.left.max ≥ i.low
4 x = x.left
5 else x = x.right
6 return x
查找与i重叠的区间x的过程中 从以x为根的树根开始,逐步向下搜索。当找到一个重叠区间 或者 x指向T.nil时过程结束。由于基本循环的每次迭代 耗费O(1)的时间,又因为n个结点的 红黑树的高度为O(lgn),所以 INTERVAL-SEARCH 过程耗费O(lgn)时间
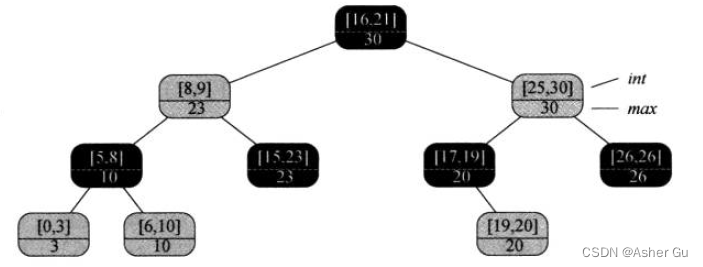
假设 要找一个与区间[22, 25]重叠的区间。开始时x为根结点,它包含区间[16, 21],与i不重叠。由于x.left.max=23 大于 i.low=22,所以这时以 这棵树根的左孩子 作为x继续循环。现在结点x包含区间[8, 9],仍不与i重叠。x.left.max=10 小于 i.low=22,因此 以x的右孩子作为新的x继续循环。现在,由于 结点x所包含的区间[15, 23]与i重叠,过程结束并返回这个结点
要明白INTERVALSEARCH的正确性, 必须理解 为什么该过程只需检查 一条由根开始的简单路径即可。该过程的基本思想是在任意结点x上,如果x.int不与i重叠,则查找 总是沿着一个安全的方向进行:如果 树中包含一个与i重叠的区间, 则该区间必定会被找到
定理:INTERVALSEARCH(T, i) 的任意一次执行,或者 返回一个其区间与i重叠的结点,或者 返回T.nil,此时 树T中没有任何结点的区间与i重叠
证明:当 x=T.nil 时while循环终止的情况
对第2~5行的while循环 使用如下的循环不变式:
如果树T 包含与i重叠的区间,那么以x为根的子树x中 将包含此区间
初始化:在第一次迭代之前,第1行置x为T的根,循环不变式成立
保持:如果 x.left=T.nil,则以x为根的子树 不会包含i重叠的区间,所以置x为 x.right 以保持 这个不变式。假设x.left≠T.nil且x.left.max < i.low。对x左子树的任一区间i’,都有
i'.high ≤ x.left.max < i.low
根据区间三分律,i和i’不重叠。因此,x的左子树不会包含与i重叠的任何区间,置x为 x.right 使循环不变式保持成立
如果在以 x.left 为根的子树中 没有与i重叠的区间,则树的其他部分 也不会包含与i重叠的区间。有x.left.max ≥ i.low,根据max属性的定义,在x的左子树中 必定存在某区间i’,满足:
i'.high = x.left.max ≥ i.low
因为i’和i’不重叠,又因为i’.high < i.low 不成立,所以根据区间三分律有:i.high < i’.low。区间树是 以区间的低端点为关键字的,所以搜索树根随意向 对x右子树中的任意区间i’,有(右子树有部分区间重叠 都没事)
i'.high < i'.low ≤ i''.low
根据区间三分律,i和i’不重叠
不管x的左子树中是否存在与i重叠的区间,置x为x.left保持循环不变式成立
终止:如果循环在 x=T.nil 时终止,则表明在以x为根的子树中,没有与i重叠的区间。循环不变式的对等情况 说明了 T中不包含与i重叠的区间,故返回 T.nil 是正确的
4、作用于区间树的结点且在 O(1) 时间内 更新max属性的过程LEFT-ROTATE的伪代码:

LEFT-ROTATE(T, x)
y = x.right
x.right = y.left
if y.left ≠ T.nil
y.left.p = x
y.p = x.p
if x.p == T.nil
T.root = y
elseif x == x.p.left
x.p.left = y
else x.p.right = y
y.left = x
x.p = y
// 下两行区别
y.max = x.max
x.max = max(x.int.high, x.left.max, x.right.max)
5、改写 INTERVAL-SEARCH 的代码,使得当所有区间都是开区间时,它也能正确地工作
INTERVAL-SEARCH(T, i)
x = T.root
while x ≠ T.nil and i does not overlap x.int
if x.left ≠ T.nil and x.left.max > i.low // 闭区间变开区间唯一区别:>=变成>
x = x.left
else x = x.right
return x
对一个给定的区间i,返回一个与i重叠且具有最小低端点的区间;或者当这样的区间不存在时返回T.nil
MIN-INTERVAL-SEARCH(T, i)
x = INTERVAL-SEARCH(T, i)
while x ≠ T.nil and i overlap x.left.int // 求最小,只要考虑左子树的区间就行
x = x.left
return x
6、给定一棵区间树T和一个区间i,描述如何在 O(min(n,klgn)) 时间内 列出T中 所有与i重叠的区间(之前只要找一个),其中k为输出的区间数
ALL-INTERVAL-SEARCH(T, i)
QUEUE Q
ENQUEUE(Q, T.root)
ARRAY A
while !QUEUE-EMPTY(Q)
x = DEQUEUE(Q)
if i overlap x.int
PUSH(A, x)
if x.left ≠ T.nil and x.left.max ≥ i.low // 区别
ENQUEUE(Q, x.left)
if x.right ≠ T.nil and x.int.low ≤ i.high // 区别
ENQUEUE(Q, x.right)
return A
需要对 树有可能的部分 进行完整的遍历,中间满足条件的加入(各个结点的low是有序的,high不是)
7、对区间树T和一个区间i,修改有关区间树的过程 来支持新的操作 INTERVAL-SEARCH-EXACTLY(T,i),它返回一个指向T中结点x的指针,使得 x.int.low = i.low 且 x.int.high = i.high;或者,如果T 不包含这样的区间时 返回T.nil。所有的操作(包括INTERVAL-SEARCH-EXACTLY)对于包含n个结点的区间树的运行时间 都应为 O(lgn)
如果 x.left.max >= i.low 还找不到,不代表 i’.low > i.high,可能 有重叠但是不相等
8、说明如何维护一个支持操作MIN-GAP的一些数的动态集合Q,使得该操作能输出Q中 两个最接近的数之间的差值。例如Q={1, 5, 9, 13, 22},则MIN-GAP返回 18-15=3,因为15和18是Q中两两个接近的数。要使得操作INSERT, DELETE,SEARCH和MIN-GAP尽可能亢效. 并分析它们的运行时间
1)数据结构选择
选择一种平衡二叉搜索树,例如红黑树。红黑树的基本性质使得插入、删除和搜索操作都能够在O(log n)的时间内完成。为了支持MIN-GAP操作,需要在每个结点中存储一些额外的信息
2)扩展红黑树
在每个结点中增加以下额外信息:
- min_gap:该子树中任意两个相邻元素之间的最小差值。
- left_max:该子树中左子树的最大元素。
- right_min:该子树中右子树的最小元素。
3)插入操作(INSERT)
插入操作和标准红黑树插入操作类似,但需要在插入后更新相关结点的min_gap、left_max和right_min信息
def insert(root, key):
# 标准红黑树插入操作
root = rb_insert(root, key)
# 更新min_gap, left_max, right_min
update_info(root)
return root
def update_info(node):
if not node:
return
# 更新左子树和右子树的信息
update_info(node.left)
update_info(node.right)
node.left_max = max(node.left.left_max if node.left else float('-inf'), node.key)
node.right_min = min(node.right.right_min if node.right else float('inf'), node.key)
left_gap = node.key - (node.left_max if node.left else float('-inf'))
right_gap = (node.right_min if node.right else float('inf')) - node.key
node.min_gap = min(left_gap, right_gap, node.left.min_gap if node.left else float('inf'), node.right.min_gap if node.right else float('inf'))
4)删除操作(DELETE)
删除操作和标准红黑树删除操作类似,但需要在删除后更新相关结点的min_gap、left_max和right_min信息
def delete(root, key):
# 标准红黑树删除操作
root = rb_delete(root, key)
# 更新min_gap, left_max, right_min
update_info(root)
return root
5)搜索操作(SEARCH)
搜索操作不需要额外修改,直接使用红黑树的搜索操作,时间复杂度为O(log n)
6)MIN-GAP操作
MIN-GAP操作只需要返回根结点的min_gap属性即可
def min_gap(root):
return root.min_gap if root else float('inf')
9、运行时间分析
INSERT: 插入操作需要O(log n)的时间来插入结点,并且在回溯时更新min_gap、left_max和right_min属性,故总时间复杂度为O(log n)
DELETE: 删除操作需要O(log n)的时间来删除结点,并且在回溯时更新min_gap、left_max和right_min属性,故总时间复杂度为O(log n)
SEARCH: 搜索操作在红黑树中需要O(log n)的时间
MIN-GAP: MIN-GAP操作只需要访问根结点的min_gap属性,时间复杂度为O(1)