self-attention机制介绍及其计算步骤
- 前言
- 一、介绍和意义
- 二、 计算细节
- 2.1 计算Attention Score
- 2.2 计算value
- 2.3 计算关联结果b
- 2.4 统一计算
- 三、总结
前言
Transformer是一种非常常见且强大的深度学习网络架构,尤其擅长处理输出为可变长度向量序列的任务,如自然语言处理(NLP)和图(Graph)处理。Transformer采用了self-attention机制,克服了传统循环神经网络(RNN)在处理长序列时存在的梯度消失和并行计算困难的问题。本文将详细介绍self-attention机制的定义和计算细节。
如果觉得该笔记对您有用的话,可以点个小小的赞,或者点赞收藏关注一键三连ヾ(◍’౪`◍) ~ 谢谢!!
一、介绍和意义
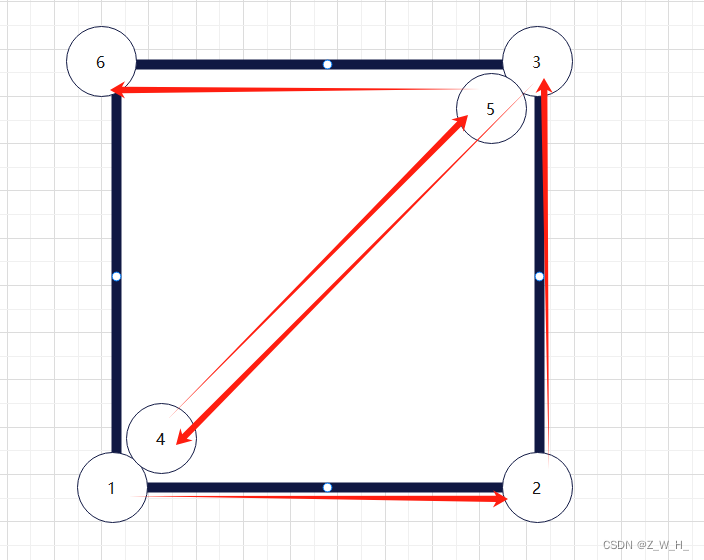
Self-attention是一种计算输入序列中每个元素对其他所有元素的重要性权重的方法。它主要用于捕捉序列数据(如文本)中的长期依赖关系和上下文信息。尽管类似的功能可以通过全连接层(fully-connected layer)实现,但当输入长度非常大时,全连接层的参数计算量会爆炸性增加,导致计算负担过大。以下图为例,当输入为4个节点时,全连接层的计算量已经非常巨大(箭头数量),可以想象当输入增多后的计算量。
为了解决以上问题,Self-attention便被提了出来。主要计算步骤如下(注意在本文中,所有的计算公式都是基于上图中四个输入(这四个输入将在一个向量中)的例子,即输入为
a
1
,
a
2
,
a
3
,
a
4
a_1,a_2,a_3, a_4
a1,a2,a3,a4)。
二、 计算细节
2.1 计算Attention Score
Self-attention用于捕捉上下文信息,因此引入了注意力分数(Attention Score)
α
\alpha
α。给
α
\alpha
α加上下标后,就可以代表任意两个节点之间的关联程度了。比如
α
1
,
2
\alpha{_1,_2}
α1,2代表了节点a1和a2之间的关联程度。为计算关联程度因子
α
\alpha
α,我们引入了三个向量Query, Key和Value,分别用首字母q,k,v来表示。这里首先介绍q,k和
α
\alpha
α的计算公式:
q
i
=
W
q
⋅
a
i
k
j
=
W
k
⋅
a
j
α
i
,
j
=
q
i
⋅
k
j
q^i = W^q \cdot a^i \\ k^j = W^k \cdot a^j \\ \alpha{_i,_j} = q^i \cdot k^j
qi=Wq⋅aikj=Wk⋅ajαi,j=qi⋅kj
解释:首先对于每个输入
a
i
a^i
ai(如单词的嵌入),通过乘上
W
q
W^q
Wq获得对应的
q
i
q^i
qi,之后对任意输入
a
j
a^j
aj乘上
W
k
W^k
Wk获得
k
j
k^j
kj,将这两个值相乘即可获得输入
a
i
a^i
ai和
a
j
a^j
aj的关联程度,即注意力分数为
α
i
,
j
=
q
i
⋅
k
j
\alpha{_i,_j} = q^i \cdot k^j
αi,j=qi⋅kj。如下图所示。
当然输入
a
i
a^i
ai也可以用自己的q乘k得到自己与自己的关联程度,比如
α
1
,
1
\alpha{_1,_1}
α1,1可由
q
1
⋅
k
1
q^1 \cdot k^1
q1⋅k1计算得到。最后,将得到的结果输入一个softmax层中,使用softmax函数对注意力分数进行归一化,得到每个输入节点对其他输入向量的权重,即获得处理后的attention sore
α
′
\alpha^{\prime}
α′,如下图所示(右上角是softmax计算公式)。

2.2 计算value
再将向量
W
q
W_q
Wq乘上对应的输入向量a,得到对应的v值,公式为:
v
i
=
W
v
⋅
a
i
v^i = W_v \cdot a^i
vi=Wv⋅ai这与 Query 和 Key 的计算方式一致。将每个输入向量对应的v值全部计算出来,如下图所示。

2.3 计算关联结果b
最终我们可以得到Self-attention针对单个输入
a
1
a_1
a1的输出结果
b
1
b^1
b1:
b
1
=
∑
i
α
1
,
i
′
⋅
v
i
b^1 = \sum_{i} \alpha_{1,i}^{\prime} \cdot v^i
b1=i∑α1,i′⋅vi根据这个公式,我们可以看出,某个上下文向量同a1的关联程度越高,对应的值在b中的占比就越大。

2.4 统一计算
上述计算都是针对单个输入进行的,在这里我们将将输入看成一个整体,即一整个输入向量,来再次梳理整个计算步骤。
- 首先我们可以将所有输入向量统合到一起,形成一个向量为I,这里依旧用图中的4个输入为例,公式为:
I = [ a 1 a 2 a 3 a 4 ] I = [ a^{1} \ a^{2} \ a^{3} \ a^{4} ] I=[a1 a2 a3 a4] - 其次我们可以计算统一的Q,K和V:
Q = [ q 1 q 2 q 3 q 4 ] = W q ⋅ [ a 1 a 2 a 3 a 4 ] = W q ⋅ I K = [ k 1 k 2 k 3 k 4 ] = W k ⋅ [ a 1 a 2 a 3 a 4 ] = W k ⋅ I V = [ v 1 v 2 v 3 v 4 ] = W v ⋅ [ a 1 a 2 a 3 a 4 ] = W v ⋅ I Q = [ q^{1} \ q^{2} \ q^{3} \ q^{4}] = W^q \cdot [ a^{1} \ a^{2} \ a^{3} \ a^{4} ] = W^q \cdot I \\ K = [ k^{1} \ k^{2} \ k^{3} \ k^{4} ] = W^k \cdot [ a^{1} \ a^{2} \ a^{3} \ a^{4} ] = W^k \cdot I\\ V = [ v^{1} \ v^{2} \ v^{3} \ v^{4} ] = W^v \cdot [ a^{1} \ a^{2} \ a^{3} \ a^{4} ] = W^v \cdot I Q=[q1 q2 q3 q4]=Wq⋅[a1 a2 a3 a4]=Wq⋅IK=[k1 k2 k3 k4]=Wk⋅[a1 a2 a3 a4]=Wk⋅IV=[v1 v2 v3 v4]=Wv⋅[a1 a2 a3 a4]=Wv⋅I - 此时,我们可以把输入节点a1的关联分数
α
\alpha
α 写成如下公式:
[ α 1 , 1 α 1 , 2 α 1 , 3 α 1 , 4 ] = q 1 ⋅ [ k 1 k 2 k 3 k 4 ] [\alpha_{1,1} \ \alpha_{1,2} \ \alpha_{1,3} \ \alpha_{1,4} \ ] = q^1 \cdot [k^{1} \ k^{2} \ k^{3} \ k^{4}] [α1,1 α1,2 α1,3 α1,4 ]=q1⋅[k1 k2 k3 k4]同理,剩下三个输入向量的关联分数公式为:
[ α 2 , 1 α 2 , 2 α 2 , 3 α 2 , 4 ] = q 2 ⋅ [ k 1 k 2 k 3 k 4 ] [ α 3 , 1 α 3 , 2 α 3 , 3 α 3 , 4 ] = q 3 ⋅ [ k 1 k 2 k 3 k 4 ] [ α 4 , 1 α 4 , 2 α 4 , 3 α 4 , 4 ] = q 4 ⋅ [ k 1 k 2 k 3 k 4 ] [\alpha_{2,1} \ \alpha_{2,2} \ \alpha_{2,3} \ \alpha_{2,4} \ ] = q^2 \cdot [k^{1} \ k^{2} \ k^{3} \ k^{4}]\\ [\alpha_{3,1} \ \alpha_{3,2} \ \alpha_{3,3} \ \alpha_{3,4} \ ] = q^3 \cdot [k^{1} \ k^{2} \ k^{3} \ k^{4}]\\ [\alpha_{4,1} \ \alpha_{4,2} \ \alpha_{4,3} \ \alpha_{4,4} \ ] = q^4 \cdot [k^{1} \ k^{2} \ k^{3} \ k^{4}] [α2,1 α2,2 α2,3 α2,4 ]=q2⋅[k1 k2 k3 k4][α3,1 α3,2 α3,3 α3,4 ]=q3⋅[k1 k2 k3 k4][α4,1 α4,2 α4,3 α4,4 ]=q4⋅[k1 k2 k3 k4]我们可以发现,当我们把所有输入向量的关联分数放进一个向量A中时,我们会得到:
A = [ α 1 , 1 α 1 , 2 α 1 , 3 α 1 , 4 α 2 , 1 α 2 , 2 α 2 , 3 α 2 , 4 α 3 , 1 α 3 , 2 α 3 , 3 α 3 , 4 α 4 , 1 α 4 , 2 α 4 , 3 α 4 , 4 ] = [ q 1 q 2 q 3 q 4 ] ⋅ [ k 1 k 2 k 3 k 4 ] = Q T ⋅ K A = \begin{bmatrix} \alpha_{1,1} & \alpha_{1,2} & \alpha_{1,3} & \alpha_{1,4} \\ \alpha_{2,1} & \alpha_{2,2} & \alpha_{2,3} & \alpha_{2,4} \\ \alpha_{3,1} & \alpha_{3,2} & \alpha_{3,3} & \alpha_{3,4} \\ \alpha_{4,1} & \alpha_{4,2} & \alpha_{4,3} & \alpha_{4,4} \\ \end{bmatrix} = \begin{bmatrix} q^1 \\ q^2 \\ q^3 \\ q^4 \\ \end{bmatrix} \cdot \begin{bmatrix} k^1 & k^2 & k^3 & k^4 \end{bmatrix} =Q^T \cdot K A= α1,1α2,1α3,1α4,1α1,2α2,2α3,2α4,2α1,3α2,3α3,3α4,3α1,4α2,4α3,4α4,4 = q1q2q3q4 ⋅[k1k2k3k4]=QT⋅K
最后,通过softmax得到最终的注意力矩阵(Attention Matrix) A ′ A^\prime A′值:
A ′ = [ α 1 , 1 ′ α 1 , 2 ′ α 1 , 3 ′ α 1 , 4 ′ α 2 , 1 ′ α 2 , 2 ′ α 2 , 3 ′ α 2 , 4 ′ α 3 , 1 ′ α 3 , 2 ′ α 3 , 3 ′ α 3 , 4 ′ α 4 , 1 ′ α 4 , 2 ′ α 4 , 3 ′ α 4 , 4 ′ ] = s o f t m a x ( A ) A^\prime = \begin{bmatrix} \alpha_{1,1}^\prime & \alpha_{1,2}^\prime & \alpha_{1,3}^\prime & \alpha_{1,4}^\prime \\ \alpha_{2,1}^\prime & \alpha_{2,2}^\prime & \alpha_{2,3}^\prime & \alpha_{2,4}^\prime \\ \alpha_{3,1}^\prime & \alpha_{3,2}^\prime & \alpha_{3,3}^\prime & \alpha_{3,4} ^\prime\\ \alpha_{4,1}^\prime & \alpha_{4,2}^\prime & \alpha_{4,3}^\prime & \alpha_{4,4}^\prime \\ \end{bmatrix} =softmax( A ) A′= α1,1′α2,1′α3,1′α4,1′α1,2′α2,2′α3,2′α4,2′α1,3′α2,3′α3,3′α4,3′α1,4′α2,4′α3,4′α4,4′ =softmax(A) - 此时我们已经得到了整体的关联分数向量
A
′
A^\prime
A′和整体的Value向量,就可以通过相乘得到对应每输入个位置的加权和,就是整体的输出结果向量O:
O = [ b 1 b 2 b 3 b 4 ] = [ v 1 v 2 v 3 v 4 ] ⋅ A ′ = V ⋅ A ′ O = [b^1\ b^2\ b^3\ b^4] = [v^1\ v^2\ v^3\ v^4] \cdot A^\prime =V \cdot A^\prime O=[b1 b2 b3 b4]=[v1 v2 v3 v4]⋅A′=V⋅A′
三、总结
以上就是 self-attention 层的计算步骤。尽管看上去复杂,但实际上在这些计算中只有
W
q
W^q
Wq,
W
k
W^k
Wk和
W
v
W^v
Wv是需要在网络中学习的参数,输入 I 在输入层就会传递给网络,剩下的都是基于这些参数的计算。
self-attention 机制的核心在于能够并行计算,极大地提升了训练和推理效率,特别适合 GPU 加速。这是 self-attention 相比 RNN 的一个重要优势。通过 self-attention 机制,Transformer 可以在处理长序列时有效地捕捉到序列中的长期依赖关系和上下文信息,解决了传统 RNN 的一些主要问题。在下一篇文章中,我们将深入探讨 Transformer 的整体架构。