1、polyfit 多项式曲线拟合
语法
语法:p = polyfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数,该阶数是 y 中数据的最佳拟合(基于最小二乘指标)。
语法:[p,S] = polyfit(x,y,n) 还返回一个结构体 S
语法:[p,S,mu] = polyfit(x,y,n) 执行中心化和缩放以同时改善多项式和拟合算法的数值属性。
参数
x:查询点 y:查询点位置的拟合值 n:多项式拟合的次数 p:最小二乘拟合多项式系数 s:误差估计结构体 mu:中心化值和缩放值
2、将多项式与三角函数拟合
代码
x = linspace(0,4*pi,20);
y = sin(x);
p = polyfit(x,y,8);
x1 = linspace(0,4*pi,100);
y1 = polyval(p,x1);%计算多项式 p 在 x1 的每个点处的值
figure(1)
plot(x,y,'o')
hold on
plot(x1,y1)
legend('拟合点','拟合线','Location','North')视图效果

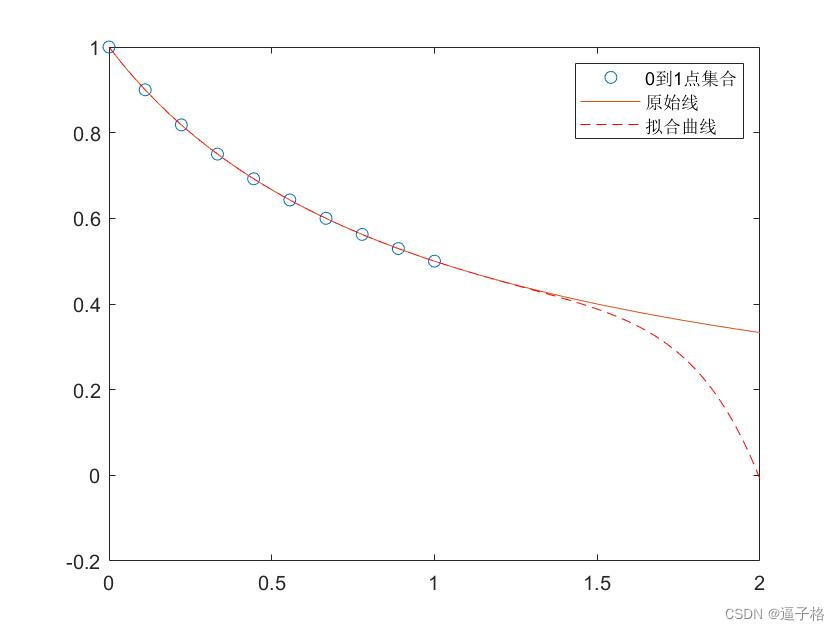
3、将多项式与点集拟合
代码
x = linspace(0,1,10);
y = 1./(1+x);
p = polyfit(x,y,7);
x1 = linspace(0,2);
y1 = 1./(1+x1);
f1 = polyval(p,x1);
figure
plot(x,y,'o')
hold on
plot(x1,y1)
plot(x1,f1,'r--')
legend('0到1点集合','原始线','拟合曲线')视图效果
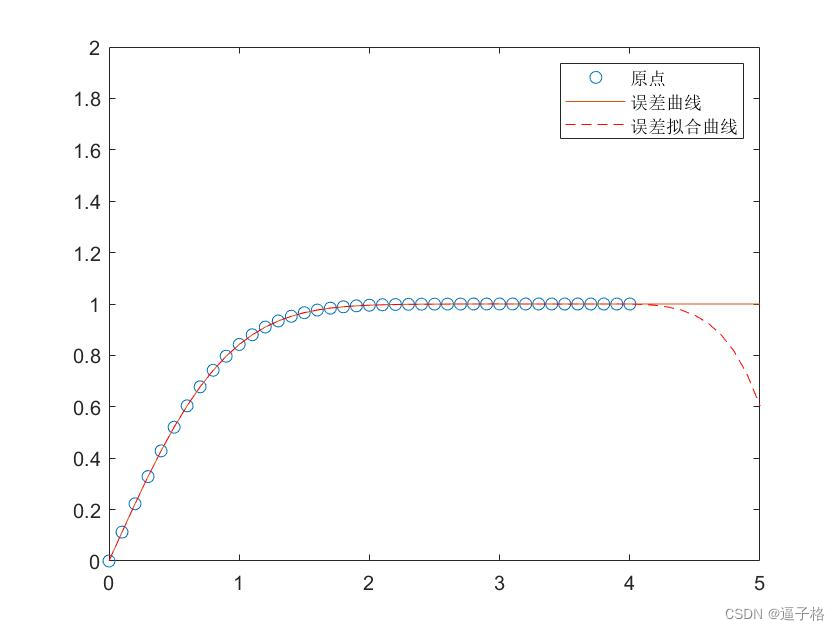
4、 对误差函数进行多项式拟合
代码
x = (0:0.1:4)';
y = erf(x);%误差函数生成误差
p = polyfit(x,y,7)
f = polyval(p,x);
x1 = (0:0.1:8)';
y1 = erf(x1);
f1 = polyval(p,x1);
figure
plot(x,y,'o')
hold on
plot(x1,y1,'-')
plot(x1,f1,'r--')
axis([0 5 0 2])
legend('原点','误差曲线','误差拟合曲线')视图效果
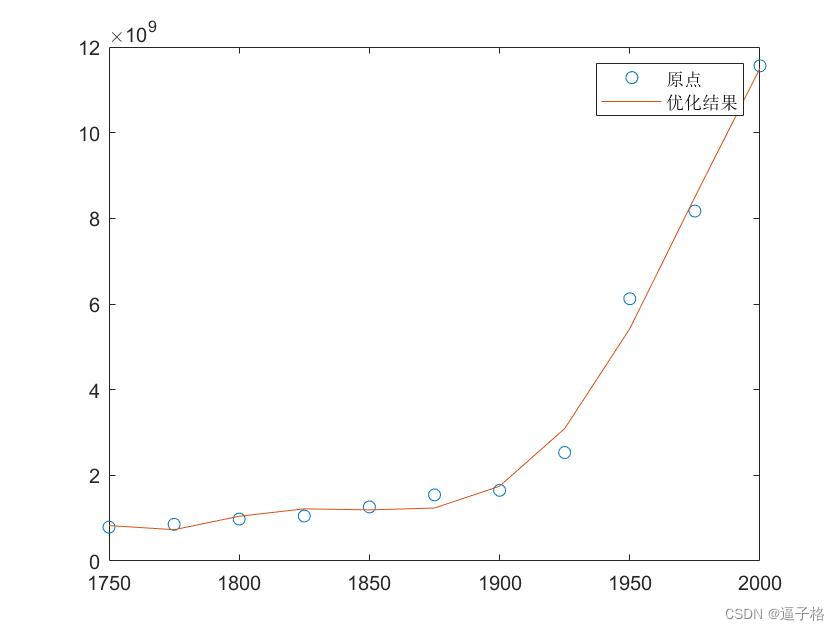
5、 使用中心化和缩放改善数值属性
代码
y = (1750:25:2000)';
pop = 1e6*[791 856 978 1050 1262 1544 1650 2532 6122 8170 11560]';
plot(y,pop,'o')
[p,~,mu] = polyfit(y, pop, 5);
f = polyval(p,y,[],mu);
hold on
plot(y,f)
legend('原点','优化结果')视图效果
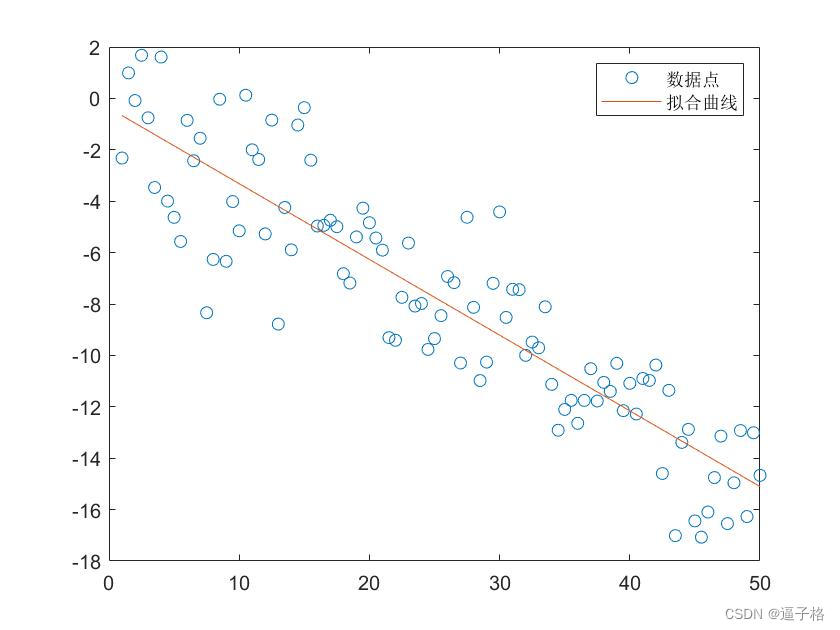
6、 简单线性回归
代码
x = 1:0.5:50;
y = -0.3*x + 2*randn(1,99);
p = polyfit(x,y,1);
f = polyval(p,x);
plot(x,y,'o',x,f,'-')
legend('数据点','拟合曲线')视图效果
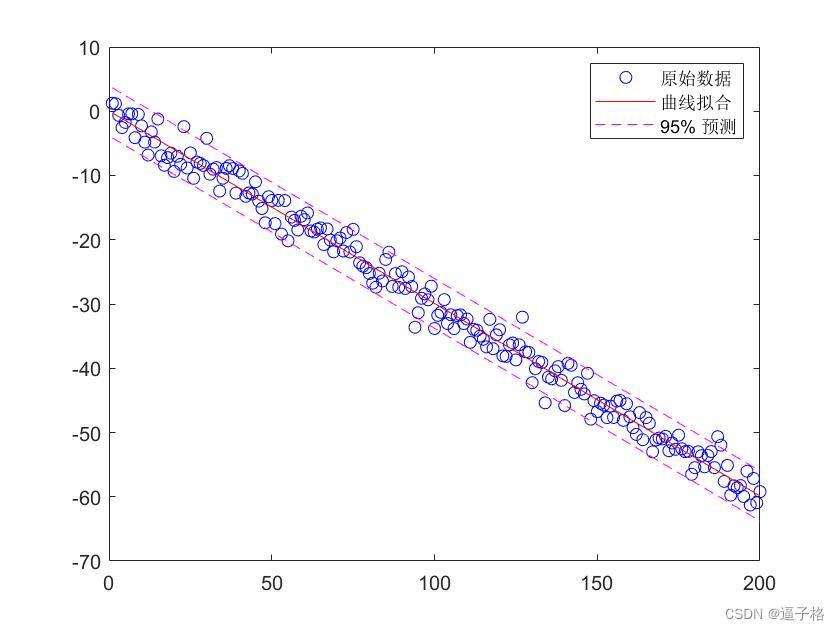
7、具有误差估计值的线性回归
代码
x = 1:200;
y = -0.3*x + 2*randn(1,200);
[p,S] = polyfit(x,y,1);
[y_fit,delta] = polyval(p,x,S);
plot(x,y,'bo')
hold on
plot(x,y_fit,'r-')
plot(x,y_fit+2*delta,'m--',x,y_fit-2*delta,'m--')
legend('原始数据','曲线拟合','95% 预测')视图效果